领域搜索算法之经典The Lin-Kernighan algorithm
- The Lin-Kernighan algorithm
- 关于算法性能提升的约束
- 参考文献
领域搜索算法是TSP问题中的三大经典搜索算法之一,另外两种分别是回路构造算法和组合算法。
而这篇文章要介绍的The Lin-Kernighan algorithm属于领域搜索算法。顾名思义,就是在已有的可行解的领域范围内进行搜索更好的解。
文章不是科普性的文章,专业性更强,开门见山。
LKH算法是对原有的3-opt算法的改进,速度更快,效率更高。
也是因为学习该算法,纠正了笔者之前对3-opt的错误理解,同时也作为学习笔记分享给大家
下面看算法的伪代码
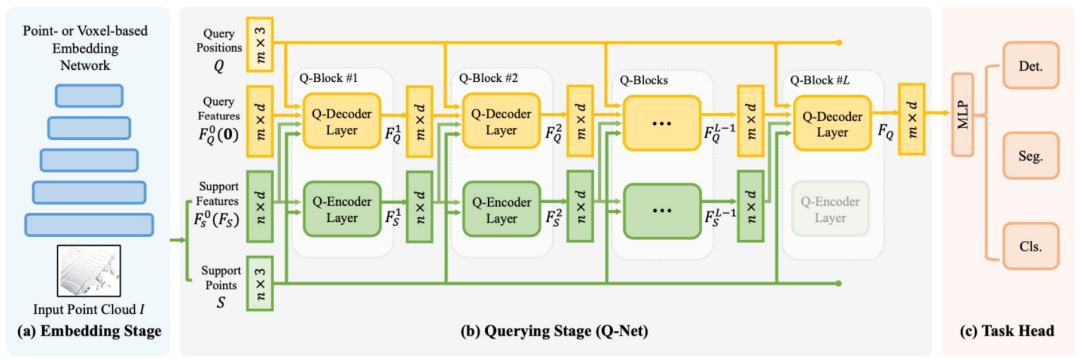
The Lin-Kernighan algorithm
需要提前说明的是
问题背景是对称的TSP问题,图是无向完全图,距离矩阵是dij对称的
T是初始可行解,T=(t1,t2,t3,…,tn)
xi,表示T中边,yi表示不属于T中的边,i可取1-n
Gi表示,将xi替换成yi所得到的收益,即总花费是否减少

1.生成初始可行解T
2.置i=1,选择t1
3 选择x1为(t1,t2)且x1属于T,是T的边(注意算法中xi都属于T,yi都不属于T,xi是要从T中删除的边,
而yi是要加入T中以形成T‘的边)
这里的==选择==是穷举出所有可能的情况
4.同样选择y1不属于T,且G1>0(G1表示删去x1,加入y1所得到的收益为正,即花销减小了)
如果不满足则跳到12
5.令 i += 1
6.在T中选择xi=(t2i-1,t2i)且满足以下的条件
①t2i可以和t1直接相连,若是这样,就可直接构成新的T’,跳到2。②ys和以xi不相等
7.选择yi=(t2i,t2i+1)且不属于T,满足下面三个条件:
①Gi收益>0。②yi != xs(s为下标)。③xi+1是存在的
且又有,如果yi存在,跳到5
8.如果y2没有被穷举完,回到7
9.如果x2没有被穷举完,回到6
10.如果y1没有被穷举完,回到4
11.如果x1没有被穷举完,回到3
12.如果t1没有被穷举完,回到3
13.停止算法或者回到步骤1
以上是对算法的解释,下面对一些有疑难的地方进行重点输出自己的解释
该算法是逐步确定3-opt算法中的三天需要交换的边,顺序是x1,y1,x2,如果收益为正,则更新,否则找x1,y1,x3。如果收益为负,继续找x1,y2,x2,继续找x1,x2,y3.这是一层一层的像栈一样的顺序,所以才会有之后8-12的回溯操作,逐步回溯到问题的最开始,就像树的分支一样。
值得注意的是:LKH算法与原始的3-opt算法不一样的是,它参加交换的第三条边是不属于T的,即自己生成的。
随着时间和研究的推进,LKH的进一步改进也涌现出来,具体可以参看参考文献
关于算法性能提升的约束
用以上LKH算法寻优的过程中,还会遇到很多极端的情况,此时可以设置一些优化算法的约束,文献中用的语言比较抽象,笔者对其进行理解翻译和解释,当然还有其他约束有待发现和补充,要介绍的约束如下:
a 交换之后可以形成闭合回路
b T‘的收益为正
c 环路是闭合的(其实a和c很大一部分是重复的)
d 先前被取出的边不能加入,先前加入过的边不能被再删除
e yi=(t2i,t2i+1)的下一条边必须是和y2i的距离是最近的5个城市之一
f 对于i>=4时,xi中i下标较小的边不能再被拆分
g 寻优截止,当收益不再为正时
h 重新构成回路的时候,连接采用贪心的连接方法
参考文献
Helsgaun K. Version 1.2 (August 2001)[J].