单调栈

给定一个整数数组 temperatures ，表示每天的温度，返回一个数组 answer ，其中 answer[i] 是指对于第 i 天，下一个更高温度出现在几天后。如果气温在这之后都不会升高，请在该位置用 0 来代替。
示例：
输入: temperatures = [73,74,75,71,69,72,76,73]
输出: [1,1,4,2,1,1,0,0]

看到 下一个较大/小元素，一定为单调栈。
需要注意的是本题存入下标较为方便，且计算的是天数差。

class Solution {
public:
    vector<int> dailyTemperatures(vector<int>& temperatures) {
        int n = temperatures.size();
        vector<int> ans(n, 0);
        stack<int> s;
        // 从后向前构建单调栈
        for (int i = n - 1; i >= 0; i--) {
            while (!s.empty() && temperatures[i] >= temperatures[s.top()]) {
                // 来大哥了，小个子失去存在意义
                s.pop();
            }
            // s不为空则说明找到了下一个大元素
            ans[i] = s.empty() ? 0 : (s.top() - i);
            s.push(i);
        }
        return ans;
    }
};

nums1 中数字 x 的 下一个更大元素 是指 x 在 nums2 中对应位置 右侧 的 第一个 比 x 大的元素。
给你两个 没有重复元素 的数组 nums1 和 nums2 ，下标从 0 开始计数，其中nums1 是 nums2 的子集。
对于每个 0 <= i < nums1.length ，找出满足 nums1[i] == nums2[j] 的下标 j ，并且在 nums2 确定 nums2[j] 的 下一个更大元素 。如果不存在下一个更大元素，那么本次查询的答案是 -1 。
返回一个长度为 nums1.length 的数组 ans 作为答案，满足 ans[i] 是如上所述的 下一个更大元素 。
示例：
输入：nums1 = [4,1,2], nums2 = [1,3,4,2].
输出：[-1,3,-1]

本题也是单调栈的经典例题，由于nums1是nums2的子集，且不存在重复元素，可以使用单调栈遍历一遍nums2得到每个元素的下个最大元素，并存在哈希表中，最后遍历一遍nums1取出哈希表的值。

class Solution {
public:
    vector<int> nextGreaterElement(vector<int>& nums1, vector<int>& nums2) {
        stack<int> s; // 单调栈
        unordered_map<int, int> m; // 哈希表用于快速查找
        for (int i = nums2.size() - 1; i >= 0; i--) {
            while (!s.empty() && nums2[i] >= s.top()) {
                s.pop();
            }
            m[nums2[i]] = s.empty() ? -1 : s.top();
            s.push(nums2[i]);
        }
        vector<int> res(nums1.size(), -1);
        // 遍历nums1
        for (int i = 0; i < nums1.size(); i++) {
            res[i] = m[nums1[i]]; // 查找对应的下一个更大元素
        }
        return res;
    }
};

给定一个循环数组 nums （ nums[nums.length - 1] 的下一个元素是 nums[0] ），返回 nums 中每个元素的 下一个更大元素 。
数字 x 的 下一个更大的元素 是按数组遍历顺序，这个数字之后的第一个比它更大的数，这意味着你应该循环地搜索它的下一个更大的数。如果不存在，则输出 -1 。
示例：
输入: nums = [1,2,1]
输出: [2,-1,2]
解释: 第一个 1 的下一个更大的数是 2；
数字 2 找不到下一个更大的数；
第二个 1 的下一个最大的数需要循环搜索，结果也是 2。

本题与上一题相比，唯一的区别在于数组变为了循环数组，对于循环数组，常用的做法是数组扩展到两倍再进行操作，但会有O(n)的空间复杂度。

class Solution {
public:
    vector<int> nextGreaterElements(vector<int>& nums) {
        // 扩展数组到两倍
        nums.insert(nums.end(), nums.begin(), nums.end());
        vector<int> res(nums.size(), -1);
        stack<int> s;
        // 单调栈模板
        for (int i = nums.size() - 1; i >= 0; i--) {
            while (!s.empty() && s.top() <= nums[i]) {
                s.pop();
            }
            res[i] = s.empty() ? -1 : s.top();
            s.push(nums[i]);
        }
        // 删除后半段
        res.erase(res.begin() + nums.size() / 2, res.end());
        return res;
    }
};

也可使用求模符号模拟构造双倍数组，i%n 从n-1到0 再从n-1到0，降低空间复杂度。

class Solution {
public:
    vector<int> nextGreaterElements(vector<int>& nums) {
        int n = nums.size();
        vector<int> res(n, -1);
        stack<int> s;
        // 假装这个数组长度翻倍 i%n 从n-1到0 再从n-1到0
        for (int i = 2 * n - 1; i >= 0; i--) {
            while (!s.empty() && s.top() <= nums[i % n]) {
                s.pop();
            }
            res[i % n] = s.empty() ? -1 : s.top();
            s.push(nums[i % n]);
        }
        return res;
    }
};

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例：
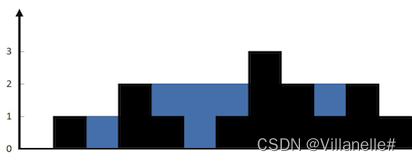
输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。

单调栈适用于解 下一个最大元素，本题可以利用单调栈的思想，构建递增单调栈（存下标），从后向前遍历，若

• 栈里有值，且当前元素大于等于栈顶元素 则 栈顶元素出栈，作为低洼区域，并记录好下标，再次判定栈里有没有值
  • 若没值，则无事发生
  • 若有值，计算w和h填平该低洼区域
• 栈里没值或当前元素小于栈顶元素 则 无事发生

最后无论什么情况当前元素都要入栈，始终保持栈的单调递增性

class Solution {
public:
    int trap(vector<int>& height) {
        stack<int> s;
        int rain = 0;
        // 递增单调栈
        for (int i = height.size() - 1; i >= 0; i--) {
            while (!s.empty() && height[s.top()] <= height[i]) {
                int lowIndex = s.top(); // 得到低洼区下标
                s.pop();
                // 栈里还有值，说明低洼区是一个水塘，填平
                if (!s.empty()) {
                    int h = min(height[i], height[s.top()]) - height[lowIndex]; // 高
                    int w = s.top() - i - 1; // 宽
                    rain += h * w;
                }
            }
            s.push(i);
        }
        return rain;
    }
};