正交投影矩阵的应用

值域与零空间

证明向量二范数

如何由已知范数构造新的范数

椭圆范数

向量范数的分析性质

向量范数的等价性

在无限维线性空间中，两个向量范数可以是不等价的。
等价性的重要意义：处理向量问题时，可以基于一种范数来建立理论，而使用另一种范数进行计算。

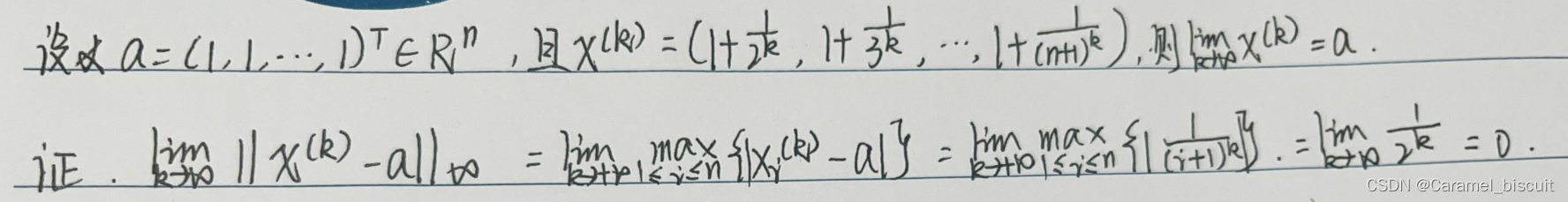
矩阵范数

P^mxn上任意两个矩阵范数均等价。

盖尔圆盘定理1的证明

定理1只说明了矩阵A的特征值均在其全部盖尔圆的并集中，而未明确哪个连通部分有几个特征值。

盖尔圆盘定理2：n阶方阵A的n个盖尔圆盘中有k个的并形成一个连通区域，且它与剩下的n-k个圆盘都不想交，则在该区域中恰好有k个特征值。

A和A^T有相同的特征值。

由两个或两个以上的盖尔圆构成的连通部分，可能在其中的一个盖尔圆中有两个或两个以上的特征值，而在另外的一个盖尔圆中没有特征值。

设n阶矩阵A的n个圆盘两两互不相交，则A相似于对角矩阵。

设n阶实阵A的n个圆盘两两互不相交，则A的特征值全为实数。
由于A为实阵，所以A的n个盖尔圆的圆心都在实轴上，又由于这些圆盘互不相交，所以A的n个特征值互不相等，且每个圆盘只含有1个特征值。
因为实矩阵若有复特征值，必成共轭对出现，且在实轴的上下方对称排列。
所以，若有一个复特征值位于A的某一盖尔圆上，则与其成共轭的特征值也必位于该圆盘上。

矩阵可逆的充要条件是0不为其特征值。

数域P的共性：

1. 数集P中的任意两个数+、-、x、÷仍然在P中。
2. 数集P中均含有数0和1。

线性空间的定义

零元素、负元素唯一。

最常见的线性空间

1. {0}是任何数域P上的线性空间。
2. 任何数域按照其加法和乘法构成本身上的一维线性空间，任何非零元构成P的一组基。R是C的子集且本身是线性空间，因此R是C的实线性空间，但R不是复线性空间的子空间。
3. 任何数域P上的mxn矩阵全体按矩阵加法和数乘构成P上的mx维线性空间，其一组基为全体基本矩阵Eij。
4. 设A是一个mxn矩阵，则齐次线性方程组Ax=0的所有解构成一个线性空间。
5. 多项式集合Pn[x]按照通常多项式的加法和数乘法。
6. [a,b]上的连续函数全体。

线性变换的本质

1. T(0) = 0 , T(-a) = -T(a)
   T(0)的几何意义：线性变换一定保持原点不动。
2. 若a1,a2,…,as线性相关，则T(a1),T(a2),…,T(as)线性相关。
3. 若T(a1),T(a2),…,T(as)线性无关，则a1,a2,…,as线性无关。

由上面的性质知：线性变换把零向量变成零向量，把x的负向量变成Tx的负向量，把线性相关的向量组变为线性相关的向量组。

线性变换的矩阵表示（如何确定一个线性变换T？）

特征向量的性质

1. 属于不同特征值的特征向量线性无关。
2. n阶矩阵A可以对角化<->A有n个线性无关的特征向量<->Cⁿ存在由A的特征向量构成的一组基<->mi=ni。