目标检测回归损失函数 IOU、GIOU、DIOU、CIOU、EIOU、Focal EIOU、alpha IOU损失函数分析

一、IOU Loss

2016文章《UnitBox: An Advanced Object Detection Network》中提出了IOU Loss将4个点构成的box看成一个整体做回归。

函数特性

IOU Loss的定义是先求出预测框和真实框之间的交集和并集之比，再求负对数，但是在实际使用中我们常常将IOU Loss写成1-IOU。如果两个框重合则交并比等于1，Loss为0说明重合度非常高。

IOU满足非负性、同一性、对称性、三角不等性，相比于L1/L2等损失函数还具有尺度不变性，不论box的尺度大小，输出的iou损失总是在0-1之间。所以能够较好的反映预测框与真实框的检测效果。

伪代码如下：

其中，

X 是预测Bounding box的面积， X^是真实Bounding box的面积， I 是两个区域的交集， U 是两个区域的并集。 L 是对IOU的交叉熵损失函数。 box位置的修正是通过对loss的反向传播迭代计算的。关于IOU Loss的反向传播具体推到过程可以移步到论文中，这里摘出结论部分如下：

其中：

从这个公式可以看出惩罚来自两个部分，预测框四个变量和预测框和真实框相交区域：

1 .损失函数和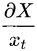成正比，因此预测的面积越大，损失越多；

2 .同时损失函数和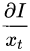成反比，因此我们希望交集尽可能的大；

根据求导公式为了减小IOU Loss，会尽可能增大相交面积同时预测更小的框。

Python实现如下：

def calculate_iou(box_1, box_2):
    """
    calculate iou
    :param box_1: (x0, y0, x1, y1)
    :param box_2: (x0, y0, x1, y1)
    :return: value of iou
    """
    # calculate area of each box
    area_1 = (box_1[2] - box_1[0]) * (box_1[3] - box_1[1])
    area_2 = (box_2[2] - box_2[0]) * (box_1[3] - box_1[1])
 
    # find the edge of intersect box
    top = max(box_1[0], box_2[0])
    left = max(box_1[1], box_2[1])
    bottom = min(box_1[3], box_2[3])
    right = min(box_1[2], box_2[2])
 
    # if there is an intersect area
    if left >= right or top >= bottom:
        return 0
 
    # calculate the intersect area
    area_intersection = (right - left) * (bottom - top)
 
    # calculate the union area
    area_union = area_1 + area_2 - area_intersection
 
    iou = float(area_intersection) / area_union
 
    return iou

Tensorflow实现如下：

def bbox_iou(self, boxes_1, boxes_2):
    """
    calculate regression loss using iou
    :param boxes_1: boxes_1 shape is [x, y, w, h]
    :param boxes_2: boxes_2 shape is [x, y, w, h]
    :return:
    """
    # transform [x, y, w, h] to [x_min, y_min, x_max, y_max]
    boxes_1 = tf.concat([boxes_1[..., :2] - boxes_1[..., 2:] * 0.5,
                         boxes_1[..., :2] + boxes_1[..., 2:] * 0.5], axis=-1)
    boxes_2 = tf.concat([boxes_2[..., :2] - boxes_2[..., 2:] * 0.5,
                         boxes_2[..., :2] + boxes_2[..., 2:] * 0.5], axis=-1)
    boxes_1 = tf.concat([tf.minimum(boxes_1[..., :2], boxes_1[..., 2:]),
                         tf.maximum(boxes_1[..., :2], boxes_1[..., 2:])], axis=-1)
    boxes_2 = tf.concat([tf.minimum(boxes_2[..., :2], boxes_2[..., 2:]),
                         tf.maximum(boxes_2[..., :2], boxes_2[..., 2:])], axis=-1)
 
    # calculate area of boxes_1 boxes_2
    boxes_1_area = (boxes_1[..., 2] - boxes_1[..., 0]) * (boxes_1[..., 3] - boxes_1[..., 1])
    boxes_2_area = (boxes_2[..., 2] - boxes_2[..., 0]) * (boxes_2[..., 3] - boxes_2[..., 1])
 
    # calculate the two corners of the intersection
    left_up = tf.maximum(boxes_1[..., :2], boxes_2[..., :2])
    right_down = tf.minimum(boxes_1[..., 2:], boxes_2[..., 2:])
 
    # calculate area of intersection
    inter_section = tf.maximum(right_down - left_up, 0.0)
    inter_area = inter_section[..., 0] * inter_section[..., 1]
 
    # calculate union area
    union_area = boxes_1_area + boxes_2_area - inter_area
 
    # calculate iou add epsilon in denominator to avoid dividing by 0
    iou = inter_area / (union_area + tf.keras.backend.epsilon())
 
    return iou

存在的问题

IOU Loss虽然解决了Smooth L1系列变量相互独立和不具有尺度不变性的两大问题，但是它也存在两个问题：

1. 预测框和真实框不相交时，不能反映出两个框的距离的远近。根据IOU定义loss等于0，没有梯度的回传无法进一步学习训练。
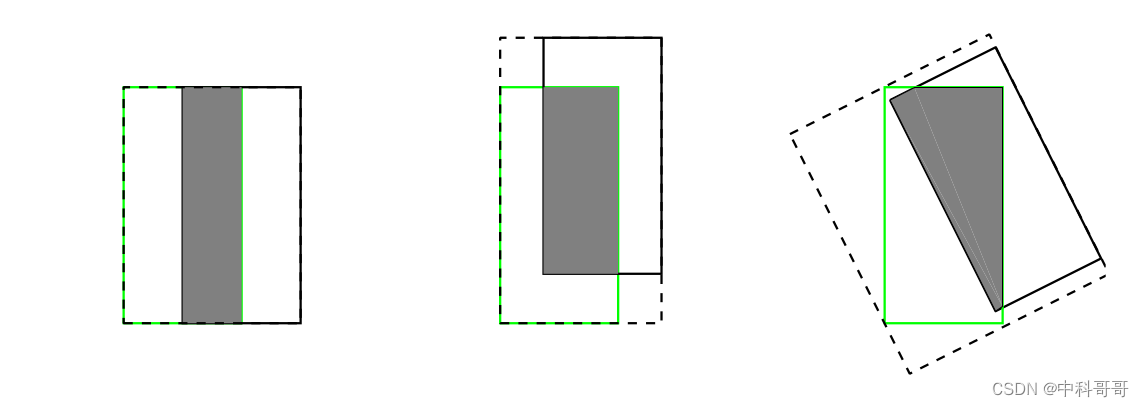
2. 预测框和真实框无法反映重合度大小。借用一张图来说，三者具有相同的IOU，但是不能反映两个框是如何相交的，从直观上感觉第三种重合方式是最差的。
   

GIOU Loss

上面指出IOU Loss的两大缺点：无法优化两个框不相交的情况；无法反映两个框如何相交的。针对此类问题斯坦福学者在2019年的文章《Generalized Intersection over Union: A Metric and A Loss for Bounding Box Regression》中提出了GIOU Loss，在IOU的基础上引入了预测框和真实框的最小外接矩形。

函数特性

GIOU作为IOU的升级版，保持了 IOU 的主要性质并避免了 IOU 的缺点，首先计算预测框

伪代码：


Python实现如下：

def calculate_giou(box_1, box_2):
    """
    calculate giou
    :param box_1: (x0, y0, x1, y1)
    :param box_2: (x0, y0, x1, y1)
    :return: value of giou
    """
    # calculate area of each box
    area_1 = (box_1[2] - box_1[0]) * (box_1[3] - box_1[1])
    area_2 = (box_2[2] - box_2[0]) * (box_1[3] - box_1[1])
 
    # calculate minimum external frame
    area_c = (max(box_1[2], box_2[2]) - min(box_1[0], box_2[0])) * (max(box_1[3], box_2[3]) - min(box_1[1], box_2[1]))
 
    # find the edge of intersect box
    top = max(box_1[0], box_2[0])
    left = max(box_1[1], box_2[1])
    bottom = min(box_1[3], box_2[3])
    right = min(box_1[2], box_2[2])
 
    # calculate the intersect area
    area_intersection = (right - left) * (bottom - top)
 
    # calculate the union area
    area_union = area_1 + area_2 - area_intersection
 
    # calculate iou
    iou = float(area_intersection) / area_union
 
    # calculate giou(iou - (area_c - area_union)/area_c)
    giou = iou - float((area_c - area_union)) / area_c
 
    return giou

Tensorflow实现如下：

def bbox_giou(self, boxes_1, boxes_2):
    """
    calculate regression loss using giou
    :param boxes_1: boxes_1 shape is [x, y, w, h]
    :param boxes_2: boxes_2 shape is [x, y, w, h]
    :return:
    """
    # transform [x, y, w, h] to [x_min, y_min, x_max, y_max]
    boxes_1 = tf.concat([boxes_1[..., :2] - boxes_1[..., 2:] * 0.5,
                         boxes_1[..., :2] + boxes_1[..., 2:] * 0.5], axis=-1)
    boxes_2 = tf.concat([boxes_2[..., :2] - boxes_2[..., 2:] * 0.5,
                         boxes_2[..., :2] + boxes_2[..., 2:] * 0.5], axis=-1)
    boxes_1 = tf.concat([tf.minimum(boxes_1[..., :2], boxes_1[..., 2:]),
                         tf.maximum(boxes_1[..., :2], boxes_1[..., 2:])], axis=-1)
    boxes_2 = tf.concat([tf.minimum(boxes_2[..., :2], boxes_2[..., 2:]),
                         tf.maximum(boxes_2[..., :2], boxes_2[..., 2:])], axis=-1)
 
    # calculate area of boxes_1 boxes_2
    boxes_1_area = (boxes_1[..., 2] - boxes_1[..., 0]) * (boxes_1[..., 3] - boxes_1[..., 1])
    boxes_2_area = (boxes_2[..., 2] - boxes_2[..., 0]) * (boxes_2[..., 3] - boxes_2[..., 1])
 
    # calculate the two corners of the intersection
    left_up = tf.maximum(boxes_1[..., :2], boxes_2[..., :2])
    right_down = tf.minimum(boxes_1[..., 2:], boxes_2[..., 2:])
 
    # calculate area of intersection
    inter_section = tf.maximum(right_down - left_up, 0.0)
    inter_area = inter_section[..., 0] * inter_section[..., 1]
 
    # calculate union area
    union_area = boxes_1_area + boxes_2_area - inter_area
 
    # calculate iou add epsilon in denominator to avoid dividing by 0
    iou = inter_area / (union_area + tf.keras.backend.epsilon())
 
    # calculate the upper left and lower right corners of the minimum closed convex surface
    enclose_left_up = tf.minimum(boxes_1[..., :2], boxes_2[..., :2])
    enclose_right_down = tf.maximum(boxes_1[..., 2:], boxes_2[..., 2:])
 
    # calculate width and height of the minimun closed convex surface
    enclose_wh = tf.maximum(enclose_right_down - enclose_left_up, 0.0)
 
    # calculate area of the minimun closed convex surface
    enclose_area = enclose_wh[..., 0] * enclose_wh[..., 1]
 
    # calculate the giou add epsilon in denominator to avoid dividing by 0
    giou = iou - 1.0 * (enclose_area - union_area) / (enclose_area + tf.keras.backend.epsilon())
 
    return giou

存在的问题

在预测框和真实框没有很好地对齐时，会导致最小外接框C的面积增大，从而使GIOU的值变小，而两个矩形框不重合时，也可以计算GIOU。GIOU Loss虽然解决了IOU的上述两个问题，但是当两个框属于包含关系时，借用下图来说：GIOU会退化成IOU，无法区分其相对位置关系。

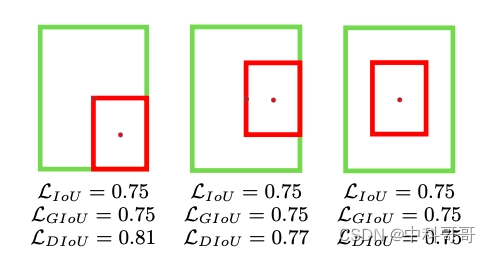
由于GIOU仍然严重依赖IOU，因此在两个垂直方向，误差很大，基本很难收敛，这就是GIoU不稳定的原因。借用下图来说：红框内部分：C为两个框的最小外接矩形，此部分表征除去两个框的其余面积，预测框和真实框在相同距离的情况下，水平垂直方向时，此部分面积最小，对loss的贡献也就越小，从而导致在垂直水平方向上回归效果较差。

DIOU Loss

针对上述GIOU的两个问题（预测框和真实框是包含关系的情况或者处于水平/垂直方向上，GIOU损失几乎已退化为IOU损失，即
导致收敛较慢）。有学者将GIOU中引入最小外接框来最大化重叠面积的惩罚项修改成最小化两个BBox中心点的标准化距离从而加速损失的收敛过程。

函数特性

DIOU损失函数公式如下：



DIOU Loss的惩罚项能够直接最小化中心点间的距离，而GIOU Loss旨在减少外界包围框的面积，所以DIOU Loss具有以下特性：

• DIOU与IOU、GIOU一样具有尺度不变性;

• DIOU与GIOU一样在与目标框不重叠时，仍然可以为边界框提供移动方向；

• DIOU可以直接最小化两个目标框的距离，因此比GIOU Loss收敛快得多；

• DIOU在包含两个框水平/垂直方向上的情况回归很快，而GIOU几乎退化为IOU；

• 当预测框和真实框完全重合时
  

当预测框和真实框不相交时

Python实现如下：

def calculate_diou(box_1, box_2):
    """
    calculate diou
    :param box_1: (x0, y0, x1, y1)
    :param box_2: (x0, y0, x1, y1)
    :return: value of diou
    """
    # calculate area of each box
    area_1 = (box_1[2] - box_1[0]) * (box_1[3] - box_1[1])
    area_2 = (box_2[2] - box_2[0]) * (box_1[3] - box_1[1])
 
    # calculate center point of each box
    center_x1 = (box_1[2] - box_1[0]) / 2
    center_y1 = (box_1[3] - box_1[1]) / 2
    center_x2 = (box_2[2] - box_2[0]) / 2
    center_y2 = (box_2[3] - box_2[1]) / 2
 
    # calculate square of center point distance
    p2 = (center_x2 - center_x1) ** 2 + (center_y2 - center_y1) ** 2
 
    # calculate square of the diagonal length
    width_c = max(box_1[2], box_2[2]) - min(box_1[0], box_2[0])
    height_c = max(box_1[3], box_2[3]) - min(box_1[1], box_2[1])
    c2 = width_c ** 2 + height_c ** 2
 
    # find the edge of intersect box
    top = max(box_1[0], box_2[0])
    left = max(box_1[1], box_2[1])
    bottom = min(box_1[3], box_2[3])
    right = min(box_1[2], box_2[2])
 
    # calculate the intersect area
    area_intersection = (right - left) * (bottom - top)
 
    # calculate the union area
    area_union = area_1 + area_2 - area_intersection
 
    # calculate iou
    iou = float(area_intersection) / area_union
 
    # calculate diou(iou - p2/c2)
    diou = iou - float(p2) / c2
 
    return diou

Tensorflow实现如下：

def bbox_diou(self, boxes_1, boxes_2):
    """
    calculate regression loss using diou
    :param boxes_1: boxes_1 shape is [x, y, w, h]
    :param boxes_2: boxes_2 shape is [x, y, w, h]
    :return:
    """
    # calculate center distance
    center_distance = tf.reduce_sum(tf.square(boxes_1[..., :2] - boxes_2[..., :2]), axis=-1)
 
    # transform [x, y, w, h] to [x_min, y_min, x_max, y_max]
    boxes_1 = tf.concat([boxes_1[..., :2] - boxes_1[..., 2:] * 0.5,
                         boxes_1[..., :2] + boxes_1[..., 2:] * 0.5], axis=-1)
    boxes_2 = tf.concat([boxes_2[..., :2] - boxes_2[..., 2:] * 0.5,
                         boxes_2[..., :2] + boxes_2[..., 2:] * 0.5], axis=-1)
    boxes_1 = tf.concat([tf.minimum(boxes_1[..., :2], boxes_1[..., 2:]),
                         tf.maximum(boxes_1[..., :2], boxes_1[..., 2:])], axis=-1)
    boxes_2 = tf.concat([tf.minimum(boxes_2[..., :2], boxes_2[..., 2:]),
                         tf.maximum(boxes_2[..., :2], boxes_2[..., 2:])], axis=-1)
 
    # calculate area of boxes_1 boxes_2
    boxes_1_area = (boxes_1[..., 2] - boxes_1[..., 0]) * (boxes_1[..., 3] - boxes_1[..., 1])
    boxes_2_area = (boxes_2[..., 2] - boxes_2[..., 0]) * (boxes_2[..., 3] - boxes_2[..., 1])
 
    # calculate the two corners of the intersection
    left_up = tf.maximum(boxes_1[..., :2], boxes_2[..., :2])
    right_down = tf.minimum(boxes_1[..., 2:], boxes_2[..., 2:])
 
    # calculate area of intersection
    inter_section = tf.maximum(right_down - left_up, 0.0)
    inter_area = inter_section[..., 0] * inter_section[..., 1]
 
    # calculate union area
    union_area = boxes_1_area + boxes_2_area - inter_area
 
    # calculate IoU, add epsilon in denominator to avoid dividing by 0
    iou = inter_area / (union_area + tf.keras.backend.epsilon())
 
    # calculate the upper left and lower right corners of the minimum closed convex surface
    enclose_left_up = tf.minimum(boxes_1[..., :2], boxes_2[..., :2])
    enclose_right_down = tf.maximum(boxes_1[..., 2:], boxes_2[..., 2:])
 
    # calculate width and height of the minimun closed convex surface
    enclose_wh = tf.maximum(enclose_right_down - enclose_left_up, 0.0)
 
    # calculate enclosed diagonal distance
    enclose_diagonal = tf.reduce_sum(tf.square(enclose_wh), axis=-1)
 
    # calculate diou add epsilon in denominator to avoid dividing by 0
    diou = iou - 1.0 * center_distance / (enclose_diagonal + tf.keras.backend.epsilon())
 
    return diou

存在的问题

虽然DIOU能够直接最小化预测框和真实框的中心点距离加速收敛，但是Bounding box的回归还有一个重要的因素纵横比暂未考虑。

CIOU Loss

CIOU Loss 和 DIOU Loss出自于2020年同一篇文章，CIOU在DIOU的基础上将Bounding box的纵横比考虑进损失函数中，进一步提升了回归精度。

函数特性

CIOU的惩罚项是在DIOU的惩罚项基础上加了一个影响因子

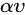这个因子把预测框纵横比拟合真实框的纵横比考虑进去。惩罚项公式如下：

Python实现如下：

def calculate_ciou(box_1, box_2):
    """
    calculate ciou
    :param box_1: (x0, y0, x1, y1)
    :param box_2: (x0, y0, x1, y1)
    :return: value of ciou
    """
    # calculate area of each box
    width_1 = box_1[2] - box_1[0]
    height_1 = box_1[3] - box_1[1]
    area_1 = width_1 * height_1
 
    width_2 = box_2[2] - box_2[0]
    height_2 = box_2[3] - box_2[1]
    area_2 = width_2 * height_2
 
    # calculate center point of each box
    center_x1 = (box_1[2] - box_1[0]) / 2
    center_y1 = (box_1[3] - box_1[1]) / 2
    center_x2 = (box_2[2] - box_2[0]) / 2
    center_y2 = (box_2[3] - box_2[1]) / 2
 
    # calculate square of center point distance
    p2 = (center_x2 - center_x1) ** 2 + (center_y2 - center_y1) ** 2
 
    # calculate square of the diagonal length
    width_c = max(box_1[2], box_2[2]) - min(box_1[0], box_2[0])
    height_c = max(box_1[3], box_2[3]) - min(box_1[1], box_2[1])
    c2 = width_c ** 2 + height_c ** 2
 
    # find the edge of intersect box
    left = max(box_1[0], box_2[0])
    top = max(box_1[1], box_2[1])
    bottom = min(box_1[3], box_2[3])
    right = min(box_1[2], box_2[2])
 
    # calculate the intersect area
    area_intersection = (right - left) * (bottom - top)
 
    # calculate the union area
    area_union = area_1 + area_2 - area_intersection
 
    # calculate iou
    iou = float(area_intersection) / area_union
 
    # calculate v
    arctan = math.atan(float(width_2) / height_2) - math.atan(float(width_1) / height_1)
    v = (4.0 / math.pi ** 2) * (arctan ** 2)
 
    # calculate alpha
    alpha = float(v) / (1 - iou + v)
 
    # calculate ciou(iou - p2 / c2 - alpha * v)
    ciou = iou - float(p2) / c2 - alpha * v
 
    return ciou

Tensorflow实现如下：

def box_ciou(self, boxes_1, boxes_2):
    """
    calculate regression loss using ciou
    :param boxes_1: boxes_1 shape is [x, y, w, h]
    :param boxes_2: boxes_2 shape is [x, y, w, h]
    :return:
    """
    # calculate center distance
    center_distance = tf.reduce_sum(tf.square(boxes_1[..., :2] - boxes_2[..., :2]), axis=-1)
 
    v = 4 * tf.square(tf.math.atan2(boxes_1[..., 2], boxes_1[..., 3]) - tf.math.atan2(boxes_2[..., 2], boxes_2[..., 3])) / (math.pi * math.pi)
 
    # transform [x, y, w, h] to [x_min, y_min, x_max, y_max]
    boxes_1 = tf.concat([boxes_1[..., :2] - boxes_1[..., 2:] * 0.5,
                         boxes_1[..., :2] + boxes_1[..., 2:] * 0.5], axis=-1)
    boxes_2 = tf.concat([boxes_2[..., :2] - boxes_2[..., 2:] * 0.5,
                         boxes_2[..., :2] + boxes_2[..., 2:] * 0.5], axis=-1)
    boxes_1 = tf.concat([tf.minimum(boxes_1[..., :2], boxes_1[..., 2:]),
                         tf.maximum(boxes_1[..., :2], boxes_1[..., 2:])], axis=-1)
    boxes_2 = tf.concat([tf.minimum(boxes_2[..., :2], boxes_2[..., 2:]),
                         tf.maximum(boxes_2[..., :2], boxes_2[..., 2:])], axis=-1)
 
    # calculate area of boxes_1 boxes_2
    boxes_1_area = (boxes_1[..., 2] - boxes_1[..., 0]) * (boxes_1[..., 3] - boxes_1[..., 1])
    boxes_2_area = (boxes_2[..., 2] - boxes_2[..., 0]) * (boxes_2[..., 3] - boxes_2[..., 1])
 
    # calculate the two corners of the intersection
    left_up = tf.maximum(boxes_1[..., :2], boxes_2[..., :2])
    right_down = tf.minimum(boxes_1[..., 2:], boxes_2[..., 2:])
 
    # calculate area of intersection
    inter_section = tf.maximum(right_down - left_up, 0.0)
    inter_area = inter_section[..., 0] * inter_section[..., 1]
 
    # calculate union area
    union_area = boxes_1_area + boxes_2_area - inter_area
 
    # calculate IoU, add epsilon in denominator to avoid dividing by 0
    iou = inter_area / (union_area + tf.keras.backend.epsilon())
 
    # calculate the upper left and lower right corners of the minimum closed convex surface
    enclose_left_up = tf.minimum(boxes_1[..., :2], boxes_2[..., :2])
    enclose_right_down = tf.maximum(boxes_1[..., 2:], boxes_2[..., 2:])
 
    # calculate width and height of the minimun closed convex surface
    enclose_wh = tf.maximum(enclose_right_down - enclose_left_up, 0.0)
 
    # calculate enclosed diagonal distance
    enclose_diagonal = tf.reduce_sum(tf.square(enclose_wh), axis=-1)
 
    # calculate diou
    diou = iou - 1.0 * center_distance / (enclose_diagonal + tf.keras.backend.epsilon())
 
    # calculate param v and alpha to CIoU
    alpha = v / (1.0 - iou + v)
 
    # calculate ciou
    ciou = diou - alpha * v
 
    return ciou

存在的问题

纵横比权重的设计还不太明白，是否有更好的设计方式有待更新。

EIOU Loss

CIOU Loss虽然考虑了边界框回归的重叠面积、中心点距离、纵横比。但是通过其公式中的v反映的纵横比的差异，而不是宽高分别与其置信度的真实差异，所以有时会阻碍模型有效的优化相似性。针对这一问题，有学者在CIOU的基础上将纵横比拆开，提出了EIOU Loss，并且加入Focal聚焦优质的锚框，该方法出自于2021年的一篇文章《Focal and Efficient IOU Loss for Accurate Bounding Box Regression》

函数特性

EIOU的惩罚项是在CIOU的惩罚项基础上将纵横比的影响因子拆开分别计算目标框和锚框的长和宽，该损失函数包含三个部分：重叠损失，中心距离损失，宽高损失，前两部分延续CIOU中的方法，但是宽高损失直接使目标盒与锚盒的宽度和高度之差最小，使得收敛速度更快。惩罚项公式如下：

代码：

from __future__ import absolute_import
from __future__ import division
from __future__ import print_function
 
import numpy as np
 
import paddle
 
from ppdet.core.workspace import register, serializable
from ..bbox_utils import bbox_iou
 
__all__ = ['IouLoss', 'GIoULoss', 'EIouLoss']
 
@register
@serializable
class Focal_EIoU_Loss(GIoULoss):
    """
    Distance-IoU Loss, see https://arxiv.org/abs/1911.08287
    Args:
        loss_weight (float): giou loss weight, default as 1
        eps (float): epsilon to avoid divide by zero, default as 1e-10
        use_complete_iou_loss (bool): whether to use complete iou loss
    """
 
    def __init__(self, loss_weight=1., eps=1e-10, use_complete_iou_loss=True):
        super(DIouLoss, self).__init__(loss_weight=loss_weight, eps=eps)
        self.use_complete_iou_loss = use_complete_iou_loss
 
    def __call__(self, pbox, gbox, iou_weight=1.):
        x1, y1, x2, y2 = paddle.split(pbox, num_or_sections=4, axis=-1)
        x1g, y1g, x2g, y2g = paddle.split(gbox, num_or_sections=4, axis=-1)
        cx = (x1 + x2) / 2
        cy = (y1 + y2) / 2
        w = x2 - x1
        h = y2 - y1
 
        cxg = (x1g + x2g) / 2
        cyg = (y1g + y2g) / 2
        wg = x2g - x1g
        hg = y2g - y1g
 
        x2 = paddle.maximum(x1, x2)
        y2 = paddle.maximum(y1, y2)
 
        # A and B
        xkis1 = paddle.maximum(x1, x1g)
        ykis1 = paddle.maximum(y1, y1g)
        xkis2 = paddle.minimum(x2, x2g)
        ykis2 = paddle.minimum(y2, y2g)
 
        # A or B
        xc1 = paddle.minimum(x1, x1g)
        yc1 = paddle.minimum(y1, y1g)
        xc2 = paddle.maximum(x2, x2g)
        yc2 = paddle.maximum(y2, y2g)
 
        intsctk = (xkis2 - xkis1) * (ykis2 - ykis1)
        intsctk = intsctk * paddle.greater_than(
            xkis2, xkis1) * paddle.greater_than(ykis2, ykis1)
        unionk = (x2 - x1) * (y2 - y1) + (x2g - x1g) * (y2g - y1g
                                                        ) - intsctk + self.eps
        iouk = intsctk / unionk
 
        # DIOU term
        dist_intersection = (cx - cxg) * (cx - cxg) + (cy - cyg) * (cy - cyg)
        dist_union = (xc2 - xc1) * (xc2 - xc1) + (yc2 - yc1) * (yc2 - yc1)
        diou_term = (dist_intersection + self.eps) / (dist_union + self.eps)
 
        
        # EIOU term
        c2_w = (xc2 - xc1) * (xc2 - xc1) + self.eps
        c2_h = (yc2 - yc1) * (yc2 - yc1) + self.eps
        rho2_w = (w - wg) * (w - wg)
        rho2_h = (h - hg) * (h - hg)
        eiou_term = (rho2_w / c2_w) + (rho2_h / c2_h)        
 
        #Focal-EIOU
        eiou = paddle.mean((1 - iouk + diou_term + eiou_term) * iou_weight)
        focal_eiou = iouk**0.5 * eiou
        return focal_eiou * self.loss_weight
 

存在的问题

没有考虑样本不平衡问题。

Focal EIOU

在BBR中，也存在训练样本不平衡的问题(one-stage检测比较突出），即由于图像中目标对象的稀疏性，回归误差小的高质量样本(锚框)的数量远远少于低质量样本(离群值)。最近的研究表明，异常值会产生过大的梯度，这对训练过程有害。 因此，让高质量的样本为网络训练过程贡献更多的梯度是至关重要的。所以引入Focal loss的提出起到很大作用，因此改进的EIOU loss( Fcoal-EIOU loss ).

函数特性

考虑到BBox的回归中也存在训练样本不平衡的问题，即在一张图像中回归误差小的高质量锚框的数量远少于误差大的低质量样本，质量较差的样本会产生过大的梯度影响训练过程。作者在EIOU的基础上结合Focal Loss提出一种Focal EIOU Loss，梯度的角度出发，把高质量的锚框和低质量的锚框分开，惩罚项公式如下：

其中IOU = |A∩B|/|A∪B|， γ为控制异常值抑制程度的参数。该损失中的Focal与传统的Focal Loss有一定的区别，传统的Focal Loss针对越困难的样本损失越大，起到的是困难样本挖掘的作用；而根据上述公式：IOU越高的损失越大，相当于加权作用，给越好的回归目标一个越大的损失，有助于提高回归精度。

代码实现：

from __future__ import absolute_import
from __future__ import division
from __future__ import print_function

import numpy as np

import paddle

from ppdet.core.workspace import register, serializable
from ..bbox_utils import bbox_iou

__all__ = ['IouLoss', 'GIoULoss', 'EIouLoss']

@register
@serializable
class Focal_EIoU_Loss(GIoULoss):
    """
    Distance-IoU Loss, see https://arxiv.org/abs/1911.08287
    Args:
        loss_weight (float): giou loss weight, default as 1
        eps (float): epsilon to avoid divide by zero, default as 1e-10
        use_complete_iou_loss (bool): whether to use complete iou loss
    """

    def __init__(self, loss_weight=1., eps=1e-10, use_complete_iou_loss=True):
        super(DIouLoss, self).__init__(loss_weight=loss_weight, eps=eps)
        self.use_complete_iou_loss = use_complete_iou_loss

    def __call__(self, pbox, gbox, iou_weight=1.):
        x1, y1, x2, y2 = paddle.split(pbox, num_or_sections=4, axis=-1)
        x1g, y1g, x2g, y2g = paddle.split(gbox, num_or_sections=4, axis=-1)
        cx = (x1 + x2) / 2
        cy = (y1 + y2) / 2
        w = x2 - x1
        h = y2 - y1

        cxg = (x1g + x2g) / 2
        cyg = (y1g + y2g) / 2
        wg = x2g - x1g
        hg = y2g - y1g

        x2 = paddle.maximum(x1, x2)
        y2 = paddle.maximum(y1, y2)

        # A and B
        xkis1 = paddle.maximum(x1, x1g)
        ykis1 = paddle.maximum(y1, y1g)
        xkis2 = paddle.minimum(x2, x2g)
        ykis2 = paddle.minimum(y2, y2g)

        # A or B
        xc1 = paddle.minimum(x1, x1g)
        yc1 = paddle.minimum(y1, y1g)
        xc2 = paddle.maximum(x2, x2g)
        yc2 = paddle.maximum(y2, y2g)

        intsctk = (xkis2 - xkis1) * (ykis2 - ykis1)
        intsctk = intsctk * paddle.greater_than(
            xkis2, xkis1) * paddle.greater_than(ykis2, ykis1)
        unionk = (x2 - x1) * (y2 - y1) + (x2g - x1g) * (y2g - y1g
                                                        ) - intsctk + self.eps
        iouk = intsctk / unionk

        # DIOU term
        dist_intersection = (cx - cxg) * (cx - cxg) + (cy - cyg) * (cy - cyg)
        dist_union = (xc2 - xc1) * (xc2 - xc1) + (yc2 - yc1) * (yc2 - yc1)
        diou_term = (dist_intersection + self.eps) / (dist_union + self.eps)

        
        # EIOU term
        c2_w = (xc2 - xc1) * (xc2 - xc1) + self.eps
        c2_h = (yc2 - yc1) * (yc2 - yc1) + self.eps
        rho2_w = (w - wg) * (w - wg)
        rho2_h = (h - hg) * (h - hg)
        eiou_term = (rho2_w / c2_w) + (rho2_h / c2_h)        

        #Focal-EIOU
        eiou = paddle.mean((1 - iouk + diou_term + eiou_term) * iou_weight)
        focal_eiou = iouk**0.5 * eiou
        return focal_eiou * self.loss_weight

存在的问题

本文针对边界框回归任务，在之前基于CIOU损失的基础上提出了两个优化方法：

将纵横比的损失项拆分成预测的宽高分别与最小外接框宽高的差值，加速了收敛提高了回归精度；
引入了Focal Loss优化了边界框回归任务中的样本不平衡问题，即减少与目标框重叠较少的大量锚框对BBox 回归的优化贡献，使回归过程专注于高质量锚框。
不足之处或许在于Focal的表达形式是否有待改进。

Alpha-IoU

论文的名字很好，反映了本文的核心想法。作者将现有的基于IoU Loss推广到一个新的Power IoU系列 Loss，该系列具有一个Power IoU项和一个附加的Power正则项，具有单个Power参数α，称这种新的损失系列为α-IoU Loss。

函数特性

文中，作者将现有的基于IoU Loss推广到一个新的Power IoU系列 Loss，该系列具有一个Power IoU项和一个附加的Power正则项，具有单个Power参数α。称这种新的损失系列为α-IoU Loss。在多目标检测基准和模型上的实验表明，α-IoU损失：

• 可以显著地超过现有的基于IoU的损失;

• 通过调节α，使检测器在实现不同水平的bbox回归精度方面具有更大的灵活性;

• 对小数据集和噪声的鲁棒性更强。

实验结果表明，α(α>1)增加了high IoU目标的损失和梯度，进而提高了bbox回归精度。

power参数α可作为调节α-IoU损失的超参数以满足不同水平的bbox回归精度，其中α >1通过更多地关注High IoU目标来获得高的回归精度(即High IoU阈值)。

**α对不同的模型或数据集并不过度敏感，在大多数情况下，α=3表现一贯良好。**α-IoU损失家族可以很容易地用于改进检测器的效果，在干净或嘈杂的环境下，不会引入额外的参数，也不增加训练/推理时间。
公式如下：

python 代码实现：

def AlphaIoU_loss(boxa, boxb, alpha):
    """
    # 除了alpha-iou,还有alpha-giou, alpha-diou, alpha-ciou，这里就不写了。
    # alpha-iou的优点是，例如alpha取2，当iou大于0.5的时候，loss的梯度是大于1的，
    # 相比iou的loss一直等于-1，收敛的更快，map0.7/map0.9有提升效果。
    loss = 1 - iou^alpha   alpha>0，取3效果比较好
    """
    inter_x1, inter_y1 = torch.maximum(boxa[:, 0], boxb[:, 0]), torch.maximum(boxa[:, 1], boxb[:, 1])
    inter_x2, inter_y2 = torch.minimum(boxa[:, 2], boxb[:, 2]), torch.minimum(boxa[:, 3], boxb[:, 3])
    inter_h = torch.maximum(torch.tensor([0]), inter_y2 - inter_y1)
    inter_w = torch.maximum(torch.tensor([0]), inter_x2 - inter_x1)
    inter_area = inter_w * inter_h
    union_area = ((boxa[:, 3] - boxa[:, 1]) * (boxa[:, 2] - boxa[:, 0])) + \
                 ((boxb[:, 3] - boxb[:, 1]) * (boxb[:, 2] - boxb[:, 0])) - inter_area + 1e-8  # + 1e-8 防止除零
    iou = inter_area / union_area

    alpha_iou = torch.pow(iou, alpha)
    alpha_iou_loss = 1 - alpha_iou
    return alpha_iou_loss

代码实现：

def bbox_alpha_iou(box1, box2, x1y1x2y2=False, GIoU=False, DIoU=False, CIoU=False, EIoU=False, alpha=3, eps=1e-9):
    # Returns tsqrt_he IoU of box1 to box2. box1 is 4, box2 is nx4
    box2 = box2.T
 
    # Get the coordinates of bounding boxes
    if x1y1x2y2:  # x1, y1, x2, y2 = box1
        b1_x1, b1_y1, b1_x2, b1_y2 = box1[0], box1[1], box1[2], box1[3]
        b2_x1, b2_y1, b2_x2, b2_y2 = box2[0], box2[1], box2[2], box2[3]
    else:  # transform from xywh to xyxy
        b1_x1, b1_x2 = box1[0] - box1[2] / 2, box1[0] + box1[2] / 2
        b1_y1, b1_y2 = box1[1] - box1[3] / 2, box1[1] + box1[3] / 2
        b2_x1, b2_x2 = box2[0] - box2[2] / 2, box2[0] + box2[2] / 2
        b2_y1, b2_y2 = box2[1] - box2[3] / 2, box2[1] + box2[3] / 2
 
    # Intersection area
    inter = (torch.min(b1_x2, b2_x2) - torch.max(b1_x1, b2_x1)).clamp(0) * \
            (torch.min(b1_y2, b2_y2) - torch.max(b1_y1, b2_y1)).clamp(0)
 
    # Union Area
    w1, h1 = b1_x2 - b1_x1, b1_y2 - b1_y1 + eps
    w2, h2 = b2_x2 - b2_x1, b2_y2 - b2_y1 + eps
    union = w1 * h1 + w2 * h2 - inter + eps
 
    # change iou into pow(iou+eps) 加入α次幂
    # alpha iou
    iou = torch.pow(inter / union + eps, alpha)
    beta = 2 * alpha
    if GIoU or DIoU or CIoU or EIoU:
        # 两个框的最小闭包区域的width和height
        cw = torch.max(b1_x2, b2_x2) - torch.min(b1_x1, b2_x1)  # convex (smallest enclosing box) width
        ch = torch.max(b1_y2, b2_y2) - torch.min(b1_y1, b2_y1)  # convex height
 
        if CIoU or DIoU or EIoU:  # Distance or Complete IoU https://arxiv.org/abs/1911.08287v1
            # 最小外接矩形 对角线的长度平方
            c2 = cw ** beta + ch ** beta + eps  # convex diagonal
            rho_x = torch.abs(b2_x1 + b2_x2 - b1_x1 - b1_x2)
            rho_y = torch.abs(b2_y1 + b2_y2 - b1_y1 - b1_y2)
            # 两个框中心点之间距离的平方
            rho2 = (rho_x ** beta + rho_y ** beta) / (2 ** beta)  # center distance
            if DIoU:
                return iou - rho2 / c2  # DIoU
 
            elif CIoU:  # https://github.com/Zzh-tju/DIoU-SSD-pytorch/blob/master/utils/box/box_utils.py#L47
                v = (4 / math.pi ** 2) * torch.pow(torch.atan(w2 / h2) - torch.atan(w1 / h1), 2)
                with torch.no_grad():
                    alpha_ciou = v / ((1 + eps) - inter / union + v)
                # return iou - (rho2 / c2 + v * alpha_ciou)  # CIoU
                return iou - (rho2 / c2 + torch.pow(v * alpha_ciou + eps, alpha))  # CIoU
 
            # EIoU 在CIoU的基础上
            # 将预测框宽高的纵横比损失项 拆分成预测框的宽高分别与最小外接框宽高的差值
            # 加速了收敛提高了回归精度
            elif EIoU:
                rho_w2 = ((b2_x2 - b2_x1) - (b1_x2 - b1_x1)) ** beta
                rho_h2 = ((b2_y2 - b2_y1) - (b1_y2 - b1_y1)) ** beta
                cw2 = cw ** beta + eps
                ch2 = ch ** beta + eps
                return iou - (rho2 / c2 + rho_w2 / cw2 + rho_h2 / ch2)
 
            # GIoU https://arxiv.org/pdf/1902.09630.pdf
            c_area = torch.max(cw * ch + eps, union)  # convex area
            return iou - torch.pow((c_area - union) / c_area + eps, alpha)  # GIoU
    else:
        return iou  # torch.log(iou+eps) or iou
 

文章贡献：

• 提出了α-IoU ，用于精确的bbox回归和目标检测，是基于IoU的现有损失的统一幂化；
• 分析了α-IoU 的一系列性质，包括次序保留、损失/梯度重加权，表明正确选择α(α >1)可以通过自适应地- 提高high IoU对象的损失和梯度的加权来提高bbox回归精度；
• 在多个基准目标检测数据集和模型上，α- iou损失优于现有的基于iou的损失，并为小数据集和噪声提供更强的鲁棒性。

IOU、GIOU、DIOU、CIOU、EIOU对比

边界框回归的三大几何因素：重叠面积、中心点距离、纵横比

• IOU Loss：考虑了重叠面积，归一化坐标尺度；
• GIOU Loss：考虑了重叠面积，基于IOU解决边界框不相交时loss等于0的问题；
• DIOU Loss：考虑了重叠面积和中心点距离，基于IOU解决GIOU收敛慢的问题；
• CIOU Loss：考虑了重叠面积、中心点距离、纵横比，基于DIOU提升回归精确度；
• EIOU Loss：考虑了重叠面积，中心点距离、长宽边长真实差，基于CIOU解决了纵横比的模糊定义，并添加Focal Loss解决BBox回归中的样本不平衡问题。

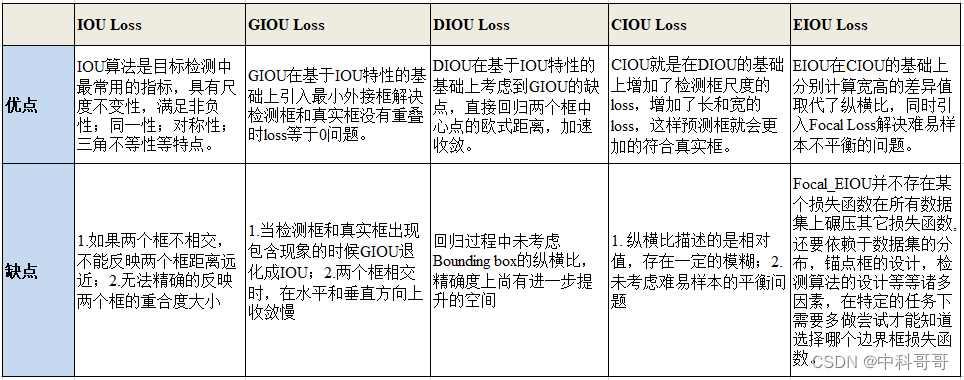
结果对比

以上损失函数性能对比：