leetcode刷题---递归思想)
- 1.1 递归介绍
- 1.2 基本步骤
- 1.3 代表题目
- 1.3.1 入门题---青蛙跳
- 1.3.2.1 初级题
- 226.翻转二叉树
- 112.路径总和
- 1.3.3 中级题---汉诺塔问题
- 1.3.4 进阶题---细胞分裂
1.1 递归介绍
如果在函数中存在着调用函数本身的情况,这种现象就叫递归。
递归的思想就是,将大问题分解为小问题来求解,然后再将小问题分解为更小的问题。这样一层层地分解,直到问题规模被分解得足够小,不用继续分解,可以直接计算结果为止。
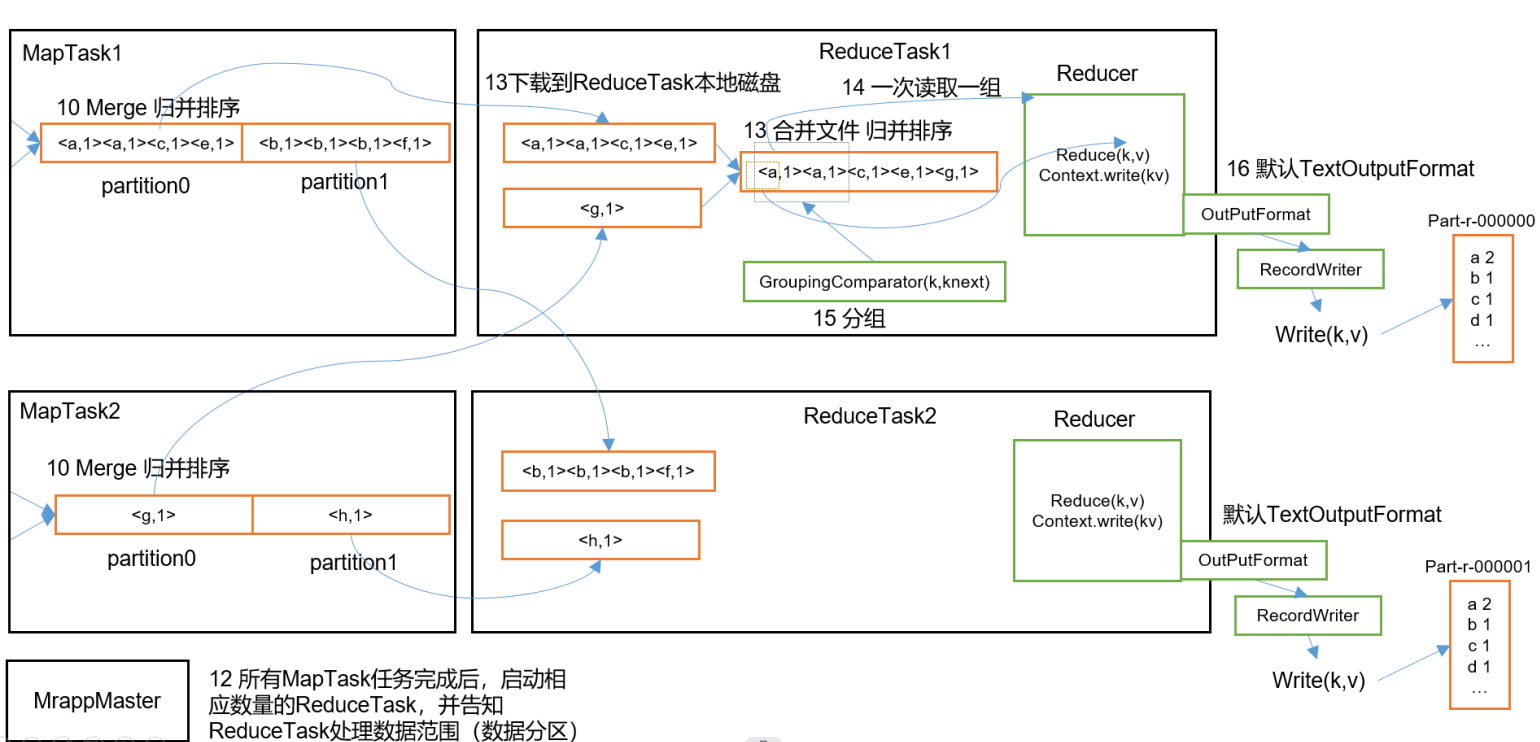
如果把这个一层层分解的过程画成图,它其实就是一颗树,叫做递归树。以斐波那契数列为例子:
def fib(n):
if n <= 1:
return 1
return fib(n - 1 ) + fib(n - 2)
递归树如下图所示:
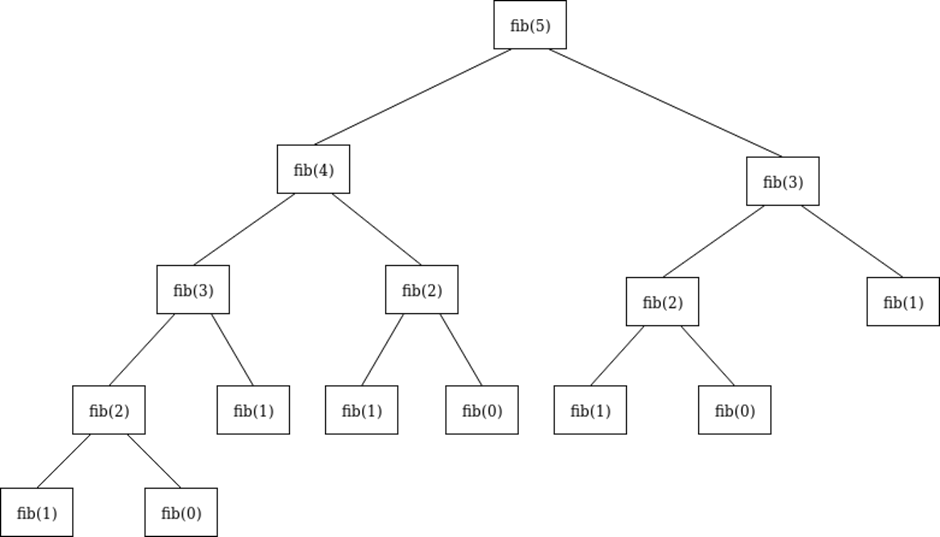
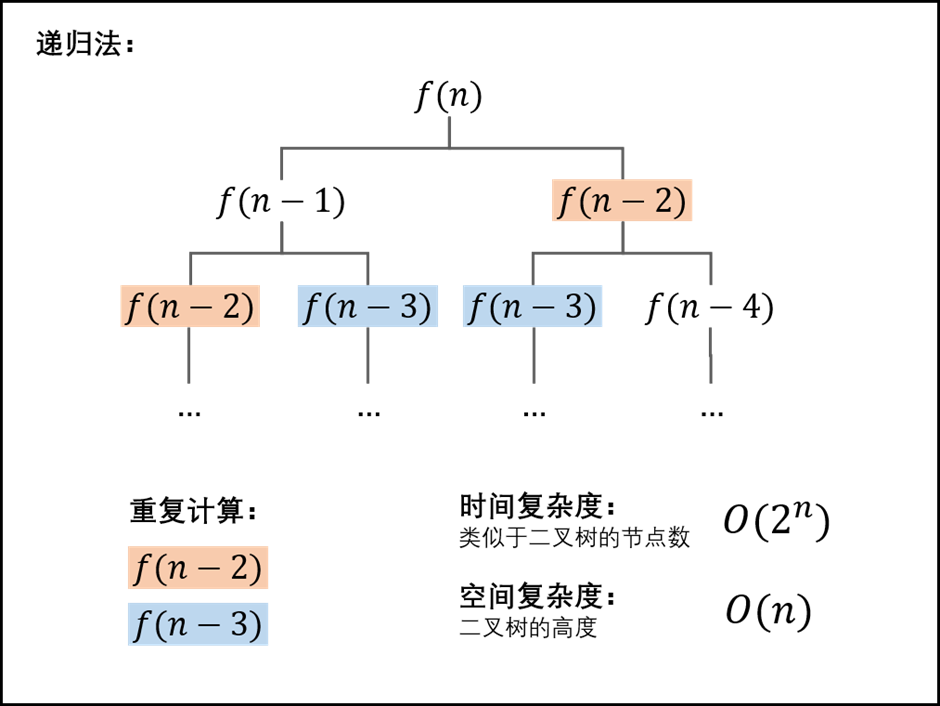
递归在“归”的过程中,符合后进先出的规则,所以需要用一个堆栈的数据结构。递归过程中函数调用会自动产生栈帧,当函数帧栈的深度越来越大的时候,栈也越来越大,如果递归没有终止条件,就会爆栈。所有基于递归思想实现的算法,第一步要思考的就是递归的终止条件。
进一步剖析「递归」,先有「递」再有「归」,「递」的意思是将问题拆解成子问题来解决, 子问题再拆解成子子问题,…,直到被拆解的子问题无需再拆分成更细的子问题(即可以求解),「归」是说最小的子问题解决了,那么它的上一层子问题也就解决了,上一层的子问题解决了,上上层子问题自然也就解决了。
递归的一般结构
def func():
if (符合边界条件):
return
# 某种形式的调用
func()
1.2 基本步骤
(1) 定义一个函数,明确函数功能
(2) 寻找问题与子问题之间的关系(递推公式)
(3) 将递推公式在定义的函数中实现
(4) 推导时间复杂度,判定是否可以接受,无法接受更换算法
1.3 代表题目
1.3.1 入门题—青蛙跳
一只青蛙可以一次跳 1 级台阶或者一次跳 2 级台阶,例如:
跳上第 1 级台阶只有一种跳法:直接跳 1 级即可。
跳上第 2 级台阶有两种跳法:每次跳 1 级,跳两次;或者一次跳 2 级。
问要跳上第 n 级台阶有多少种跳法?:
一只青蛙只能跳一步或两步台阶,自上而下地思考,也就是说如果要跳到 n 级台阶只能从 从 n-1 或 n-2 级跳 。那么从以上分析可得 f(n) = f(n-1) + f(n-2),显然这就是我们要找的问题与子问题的关系,而显然当 n = 0, n = 1, 即跳一二级台阶是问题的最终解 。
递归解法:
def numWays(n):
if n == 0 or n == 1:
return 1
return numWays(n - 1) + numWays(n - 2)
时间复杂度高,因为在递归过程中有大量的重复计算。
优化1:空间换时间
def numWays(n):
mid = [0] * (n + 1)
if n == 0 or n == 1:
return 1
mid[0] = mid[1] = 1
for i in range(2, n + 1):
mid[i] = mid[i - 1] + mid[i - 2]
return mid[n]
空间换时间,时间复杂度O(n),空间复杂度O(n)
优化2:自下而上的方法
def numWays(n):
if n == 0 or n == 1:
return 1
res = 0
pre = 1
next = 1
for i in range(2, n + 1):
res = pre + next
pre = next
next = res
return res
时间复杂度O(n),空间复杂度O(1)
简单总结一下: 分析问题我们需要采用自上而下的思维,而解决问题有时候采用自下而上的方式能让算法性能得到极大提升,思路比结论重要 。
1.3.2.1 初级题
226.翻转二叉树
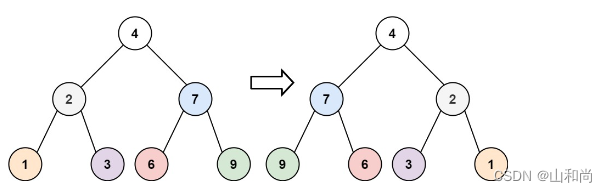
翻转(根节点) = 翻转(根节点的左节点) + 翻转(根节点的右节点) ,即 invert(root) = invert(root->left) + invert(root->right) ,递归的终止条件是当结点为叶子结点时终止(因为叶子节点没有左右结点) 。由于我们会对每一个节点都去做翻转,所以时间复杂度是 O(n), 如果是完全二叉树,空间复杂度为树的高度O(logn) 。最坏情况,如果此二叉树只有左节点,没有右节点,则树的高度即结点的个数 n,此时空间复杂度为 O(n),总的来看,空间复杂度为O(n) 。
def invertTree(self, root):
# 叶子节点不能翻转
if not root:
return root
# 翻转右节点下的左右节点
right = self.invertTree(root.right)
# 翻转左节点下的左右节点
left = self.invertTree(root.left)
# 左右节点下的二叉树翻转好后,翻转根节点的左右节点
root.left = right
root.right = left
return root
112.路径总和
给定一个二叉树和一个目标和,判断该树中是否存在根节点到叶子节点的路径,这条路径上所有节点值相加等于目标和。
说明: 叶子节点是指没有子节点的节点。
示例:
给定如下二叉树,以及目标和 sum = 22,
5
/ \
4 8
/ / \
11 13 4
/ \ \
7 2 1
返回 true, 因为存在目标和为 22 的根节点到叶子节点的路径 5->4->11->2。
是否存在一条路径,从当前节点root到叶子节点的路径和为sum,这个问题可以转化为:是否存在从当前节点的子节点到叶子的路径和为sum-子节点值。即:
hasPathSum(root,sum)=hasPathSum(root.left,sum-root.val) or hasPathSum(root.right,sum-root.val)
递归终止条件是当前节点是叶子节点,直接判断sum是否等于节点值即可。
def hasPathSum(self, root: Optional[TreeNode], targetSum: int) -> bool:
if not root:
return False
if not root.left and not root.right:
return targetSum == root.val
return self.hasPathSum(root.left, targetSum - root.val) or self.hasPathSum(root.right, targetSum - root.val)
1.3.3 中级题—汉诺塔问题
在经典汉诺塔问题中,有 3 根柱子及 N 个不同大小的穿孔圆盘,盘子可以滑入任意一根柱子。一开始,所有盘子自上而下按升序依次套在第一根柱子上(即每一个盘子只能放在更大的盘子上面)。移动圆盘时受到以下限制:
(1) 每次只能移动一个盘子;
(2) 盘子只能从柱子顶端滑出移到下一根柱子;
(3) 盘子只能叠在比它大的盘子上。
请编写程序,用栈将所有盘子从第一根柱子移到最后一根柱子。
你需要原地修改栈。
将n个圆盘经由B移到C上,可以按照以下三个步骤来分析,首先将A上面的n-1个圆盘看成是一个圆盘:
- 将A上面的n-1个圆盘经由C移到B
- 将A底下最大的圆盘移到C
- 再将B上的n-1个圆盘经由A移到C上
move(n from A to C) = move(n-1 from A to B) + move(A to C) + move(n-1 from B to C)
终止条件我们很容易看出,当 A 上面的圆盘只有一个的时候。
# 将 n 个圆盘从 a 经由 b 移动到 c 上
def hanota(A, B, C):
n = len(A)
move(n, A, B, C)
def move(n, A, B, C):
if n == 1:
C.append(A.pop())
return
# 将A上面的n-1个圆盘经由C移动到B
move(n-1, A, C, B)
# 将A底下最大的那块移动到C
C.append(A.pop())
# 将B上的n-1个圆盘经由A移动到C
move(n - 1, B, A, C)