文章目录
- 【后续会持续更新CDA Level I&II备考相关内容,敬请期待】
- 【考试大纲】
- 【考试内容】
- 【备考资料】
- 1、统计基本概念
- 1.1、统计学的含义及应用
- 1.1.1、统计学的含义
- 1.2.1、统计学的应用
- 1.2、统计学的基本概念
- 1.2.1、数据及数据的分类
- 1.2.2、总体和样本
- 1.2.3、参数和统计量
- 1.2.4、变量
- 2、数据的描述性统计
- 2.1、描述性统计图表
- 2.1.1、直方图
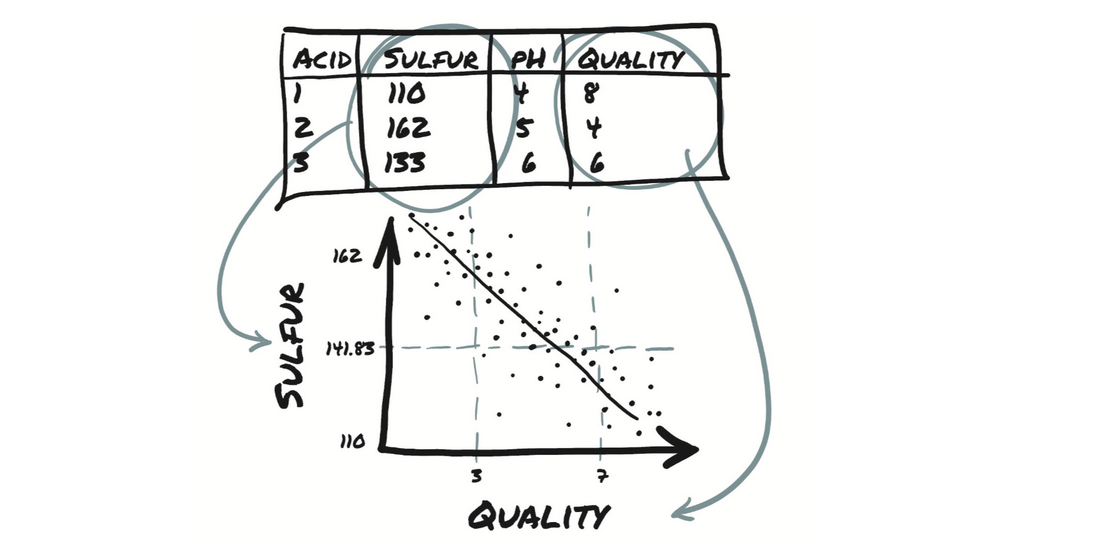
- 2.1.2、散点图
- 2.1.3、箱型图
- 3、集中趋势的描述
- 3.1、众数
- 3.2、分位数及中位数
- 3.3、平均数
- 3.4.1、算数平均数
- 3.4.2、几何平均数
- 3.4.3、调和平均数
- 4、离散程度的描述
- 4.1、极差
- 4.2、平均差
- 4.3、方差与标准差
- 4.4、离散系数
- 4.5、相对位置的度量——标准化值
- 5、分布形态的描述
- 5.1、矩的相关概念
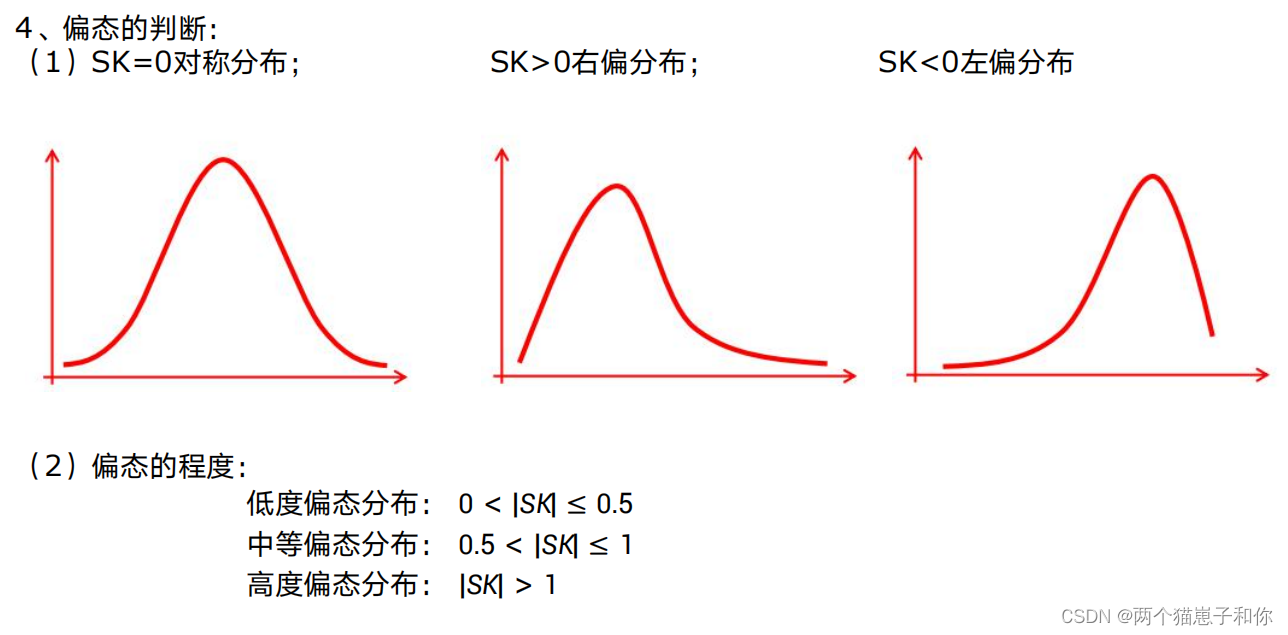
- 5.2、偏态
- 偏度计算公式的理解
- 5.3、峰态
- 峰度计算公式的理解
【后续会持续更新CDA Level I&II备考相关内容,敬请期待】
【考试大纲】

【考试内容】


【备考资料】
1、统计基本概念
1.1、统计学的含义及应用
1.1.1、统计学的含义
- 统计学的含义:统计学是一门收集、处理、分析、解释数据并从数据中得出结论的学科。
- 统计学是应用数学的一个分支,主要通过利用概率论建立数学模型,收集所观察系统的数据,进行量化的分析、总结,并进而进行推断和预测,为相关决策提供依据和参考。
- 统计学主要又分为描述统计学和推断统计学。
- 描述性统计分析:研究数据收集、处理和描述的统计学方法,如总体规模、对比关系、集中趋势、离散程度、偏态、峰态等。
- 推断性统计分析:研究如何利用样本数据来推断总体特征的统计学方法,如估计、假设检验、列联分析、方差分析、相关分析、回归分析等。
1.2.1、统计学的应用
随着计算机的发展和各种统计软件的开发,作为一门基础学科的统计学在金融、保险、生物、经济等领域得到了广泛应用
1.2、统计学的基本概念
1.2.1、数据及数据的分类
数据是统计学的分析对象。数据有不同的表现形式,也有不同的分类。
数据的表现形式:
- 数字:可以进行比较、加减乘除四则运算等,有严格的数据符号,常用阿拉伯数字表示。
- 文字:不可运算,例如男,女;好,坏等
数据的分类:
- 按照计量尺度分类
- 分类型数据:对事物进行分类的结果,特点是不可排序,不可计算。如人的性别分为:男、女
- 顺序型数据:对事物类别顺序的测度,特点是可排序,不可计算。如产品分为:一等品、二等品、三等品
- 数值型数据:对事物的精确测度,特点是可排序,可计算。如身高:175cm、180cm
- 总结:分类型数据和顺序型数据是定性数据,数值型数据是定量数据,等级自上而下。不同类型的数据之间可以进行转换,处理低级数据的方法高级数据可以用,处理高级数据的方法低级数据不能用。
- 按计量层次分类
- 定类数据:这是数据的最低层。它将数据按照类别属性进行分类,各类别之间是平等并列关系。这种数据不带数量信息,并且不能在各类别间进行排序。例如红色、白色;性别中的男、女;
- 定序数据:这时数据的中间级别。定序数据不仅可以将数据分成不同的类别,而且各类别之间还可以通过排序来比较优劣。也就是说,定序数据与定类数据最主要的区别是定序数据之间还是可以比较顺序的
- 定距数据。定距数据是具有一定单位的实际测量值(如摄氏温度、考试成绩等)。此时不仅可以知道两个变量之间存在差异,还可以通过加、减法运算准确的计算出各变量之间的实际差距是多少。
- 定比数据。这是数据的最高等级。它的数据表现形式同定距数据一样,均为实际的测量值。定比数据与定距数据唯一的区别是:在定比数据中是存在绝对零点的,而定距数据中是不存在绝对零点的(零点是人为制定的)。因此定比数据间不仅可以比较大小,进行加、减运算,还可以进行乘、除运算。
- 按来源不同分类
- 直接来源:一手数据,原始资料
- 间接来源:二手资料,次级资料
- 按收集方式不同分类:
- 观测数据
- 实验数据
- 按与时间的关系不同分类:
- 时间序列数据:它是指在不同的时间上搜集到的数据,反映现象随时间变化的情况。
- 截面型数据。它是指在相同的或近似的时间点上搜集到的数据,描述现象在某一时刻的变化情况。
- 面板数据(混合数据、平行数据):截面型数据。它是指在相同的或近似的时间点上搜集到的数据,描述现象在某一时刻的变化情况。
- 按概型不同分类:
- 离散型数据
- 连续型数据
- 特殊的数据类型:虚拟变变量数据,在数据集中可能以集中方式出现
- 可以反映数据的固有属性,如一家公司属于医疗行业(虚拟变量=1),或者不属于医疗行业(虚拟变量=0) ;
- 可能是数据的一个识别特征。可以通过一个为真或者为假的条件来引入这样的二进制变量。例如日期可能在2008年之前(金融危机爆发前,虚拟变量= 0),也可能在2008年之后(金融危机爆发后,虚拟变量= 1)
- 可以由数据的某些特征构建。虚拟变量将反映一个或真或假的条件。比如特定的公司规模(如果营收超过10亿元,虚拟变量= 1,否则= 0)
1.2.2、总体和样本
- 总体(population):指研究的所有元素的集合,其中每个元素称为个体。例如研究全校学生的平均年龄,总体是全校学生。和总体相关的事物,统计学上用希腊字母表示。
- 样本(sample):从总体中抽取的一部分元素的集合。实际中,总体的个体往往难以一一研究,所以可以从中抽取一部分来进行研究。例如研究全校学生的平均年龄,总体过大,从中抽取100人进行研究,样本就是抽取的这100个学生。和样本相关的事物,统计学上用英文字母表示。
- 样本容量:构成样本的元素的数目称为样本容量。上面的例子中,100就是样本容量。
1.2.3、参数和统计量
-参数(parameter):指研究者想要了解的总体的某种特征值,主要有总体均值(μ)、总体标准差(σ)、总体比例(π)等。
- 统计量(statistic):指根据样本数据计算出来的一个量,即样本的某个特征值。常见的统计量有样本均值(x)、样本标准差(S)、样本比例(p)等。
1.2.4、变量
- 概念:指描述实木某种特征的概念。如商品销售额、受教育程度、产品的质量等级等。
- 变量与数据的关系:变量的具体表现称为变量值,即数据。
- 变量的分类:根据变量的数据计量尺度不同来分
- 分类变量(categorical variable):说明事物类别的一个名称;
- 顺序变量(rank variable):说明事物有序类别的一个名称;
- 数值型变量(metric variable):说明事物数据特征的一个名称。
2、数据的描述性统计
- 总量指标:反映一定时间、空间下某种现象的总体规模、总水平或总成功的统计指标。
- 相对指标:是两个有相互联系的指标数值之比,例如目标完成率
2.1、描述性统计图表
建议大家多看些分析案例,有好的分析案例的练习,希望大佬们分享给我,谢谢~~
构成类图标主要突出的是部分在整体中的占比关系,饼图属于构成类图表;散点图属于描述类图表;折线图属于序列类图表;条形图属于比较类图表;词云图是比较类图表
2.1.1、直方图
【篇幅过长,收集在专栏下的《描述性统计图表——直方图》中】传送门 ↓↓↓
《描述性统计图表——直方图》
2.1.2、散点图
【篇幅过长,收集在专栏下的《描述性统计——散点图》中】传送门 ↓↓↓
《描述性统计图表——散点图》
2.1.3、箱型图
【篇幅过长,收集在专栏下的《描述性统计——箱线图》中】传送门 ↓↓↓
《描述性统计图表——箱线图》
3、集中趋势的描述

3.1、众数
众数(Mode)是指在统计分布上具有明显集中趋势点的数值,代表数据的一般水平。 也是一组数据中出现次数最多的数值,有时众数在一组数中有好几个。用M表示。
3.2、分位数及中位数
详细定义见:《描述性统计图表——箱线图》
3.3、平均数
对于同一组数据,一定满足:算数平均数>=几何平均数>=调和平均数,当所有数据取至相同的时候,等号成立;
3.4.1、算数平均数

加权平均数例题:
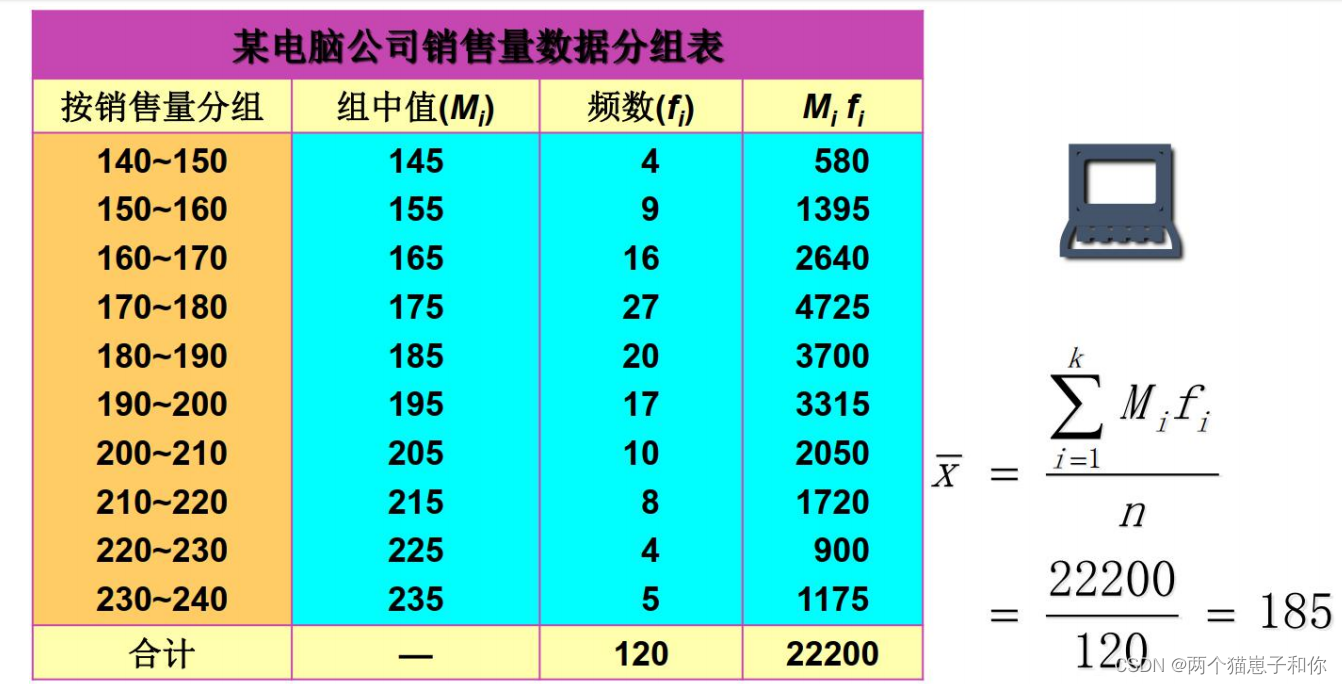
3.4.2、几何平均数


3.4.3、调和平均数

4、离散程度的描述
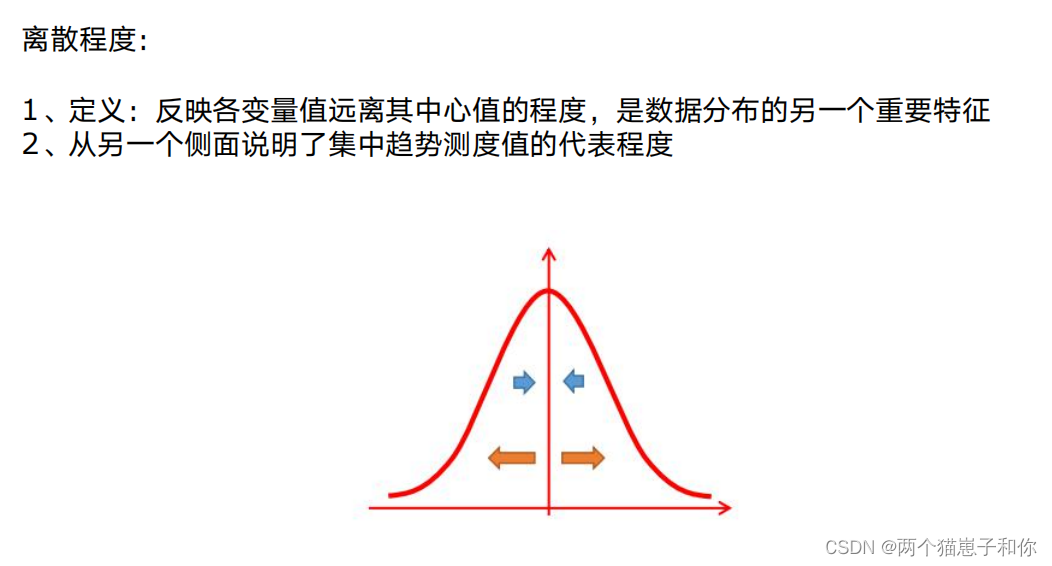
4.1、极差

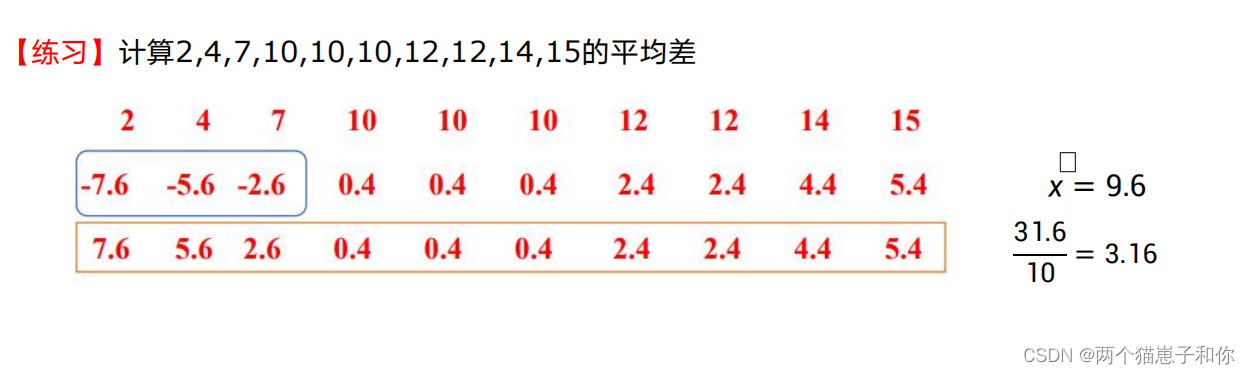
4.2、平均差

4.3、方差与标准差



自由度(degree of freedom, df)指的是计算某一统计量时,取值不受限制的变量个数。通常df=n-k。其中n为样本数量,k为被限制的条件数或变量个数,或计算某一统计量时用到其它独立统计量的个数。自由度通常用于抽样分布中。
4.4、离散系数
离散系数又称变异系数,是统计学当中的常用统计指标。离散系数是测度数据离散程度的相对统计 量,主要是用于比较不同样本数据的离散程度。离散系数大,说明数据的离散程度也大;离散系数小,说明数据的离散程度也小

4.5、相对位置的度量——标准化值
标准化:z=(z-样本均值)/样本标准差


切比雪夫不等式


5、分布形态的描述
5.1、矩的相关概念
- k阶原点矩,又叫k阶矩:E(Xk),也就是随机变量X的k次方的均值;
- k阶中心矩:E{[X-E(X)]k},也就是随机变量X与X的均值的差的k次方形成的新的随机变量的均值;
- k+l混合矩:E(XkYl):也就是随机变量X的k次方与随机变量Y的l次方形成的新的随机变量的均值。
- k+l混合中心矩:E{[E-E(X)]k[Y-E(Y)]l}:也就是随机变量X与X的均值的差的k次方乘以随机变量Y与Y的均值的差的l次方后乘积形成的新的随机变量的均值。
5.2、偏态
扩展知识——偏态分布:偏态分布
偏度(skewness)也称为偏态、偏态系数,是统计数据分布偏斜方向和程度的度量,是统计数据分布非对称程度的数字特征。一般来说,偏度的绝对值超过0.5,意味着偏度非常大。在风险管理当中,较大程度的负偏是需要格外关注的问题,因为这可能导致大的损失的发生。
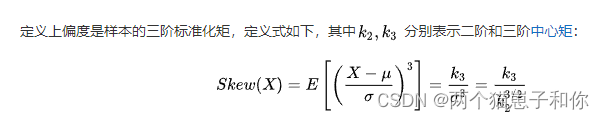

偏度计算公式的理解
- 对于未分组数据:求出样本均值、方差以及标准差。
- 分母=(样本容量-1)(样本容量-2)*标准差的三次方;
- 分子=样本容量*[(每个样本值-样本均值)3的累计值]
- 对于分组数据:求出加权算数平均数,根据加权算数平均数算出方差以及标准差。
- 加权算数平均数

- 方差及标准差
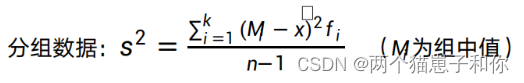
- 分母=样本容量*样本标准差3
- 分子=(组中值-样本均值)3与频数乘积得到的值的累加

- 加权算数平均数
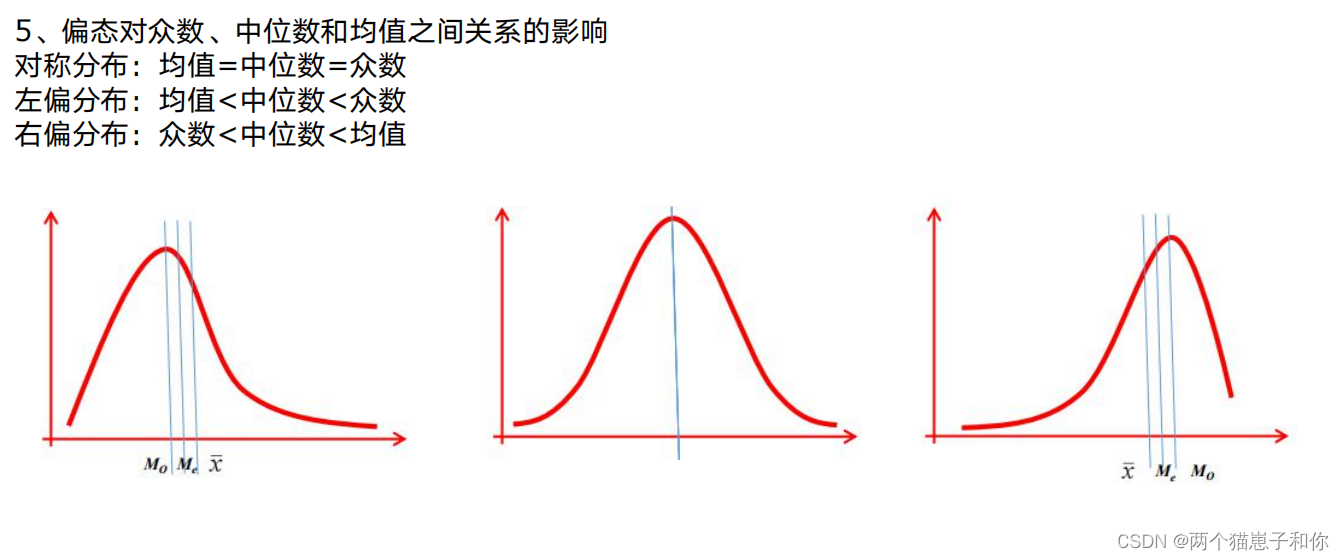
正态分布的偏度为0,两侧尾部长度对称。若以bs表示偏度。bs<0称分布具有负偏离,也称左偏态,此时数据位于均值左边的比位于右边的少,直观表现为左边的尾部相对于与右边的尾部要长,因为有少数变量值很小,使曲线左侧尾部拖得很长;bs>0称分布具有正偏离,也称右偏态,此时数据位于均值右边的比位于左边的少,直观表现为右边的尾部相对于与左边的尾部要长,因为有少数变量值很大,使曲线右侧尾部拖得很长;而bs接近0则可认为分布是对称的。若知道分布有可能在偏度上偏离正态分布时,可用偏离来检验分布的正态性。右偏时一般算术平均数>中位数>众数,左偏时相反,即众数>中位数>平均数。正态分布三者相等。
5.3、峰态
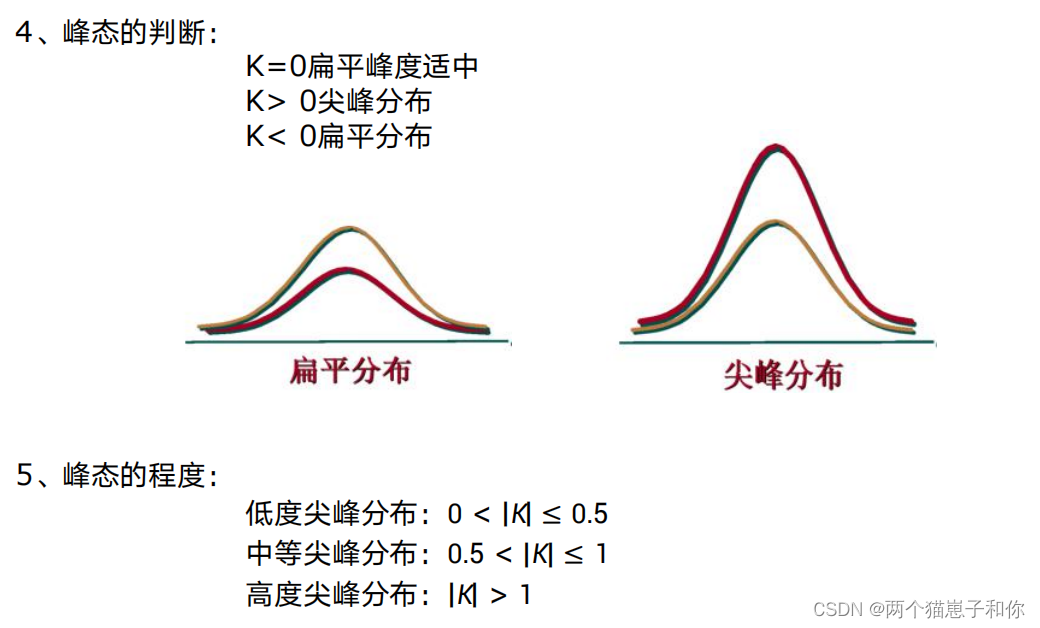
峰态(kurtosis)一词是由统计学家皮尔逊于1905年首次提出的。它是对数据分布平峰或尖峰程度的测度。测度峰态的统计量则是峰态系数(coefficient of kurtosis),记作K。峰态通常是与标准正态分布相比较而言的。如果一组数据服从标准正态分布,则峰态系数的值等于0;若峰态系数的值明显不等于0,则表明分布比正态分布更平或更尖,通常称为平峰分布或尖峰分布。
对于峰度而言,尖峰态的峰度大于3,低峰态的峰度小于3,而正态分布的峰度正好等于3。有的峰度的计算公式当中,直接在计算公式中减去了3。那么就变成了尖峰态的峰度大于0,低峰态的峰度小于0,而正态分布的峰度等于0。


峰度计算公式的理解
- 对于未分组数据:求出样本均值、方差以及标准差。
- 分母=(样本容量-1)(样本容量-2)(样本容量-3)*标准差的四次方;
- 分子=样本容量*(样本容量+1)[(每个样本值-样本均值)4的累计值]-3倍的[样本值与样本均值的差的平方和]2(样本容量-1)
- 对于分组数据:求出加权算数平均数,根据加权算数平均数算出方差以及标准差。
- 加权算数平均数

- 方差及标准差
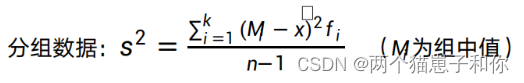
- 分母=样本容量*样本标准差3
- 分子=(组中值-样本均值)4与频数乘积得到的值的累加-3倍的样本容量*样本标准差4
- 加权算数平均数

较高的峰度通常表明数据的变动是由一些极值相对于期望的变动引起的,而非许多相对较小的差异。