前言
一、DropOut简介
- 1-1、DropOut论文图解
- 1-2、DropOut介绍
- 1-3、DropOut产生动机
- 1-4、DropOut流程简介
二、模型描述
- 2-1、公式描述
- 2-2、神经网络图描述
- 2-3、一些需要注意的问题！
三、Dropout代码实现以及相关变种（部分有实现）
- 3-1、Dropout实现（Torch实现）
- 3-2、Dropout实现（Numpy实现，训练集乘以1/(1-p)，测试集不做变化）
- 3-3、Dropout实现（Numpy实现，测试集变化）
- 3-4、Dropout实现（复写一个类似于Pytorch中的Dropout）
- 3-5、高斯Dropout
- 3-6、DropConnect
- 3-7、Standout
附录1、nn.Linear()详解
总结

前言

深度神经网络包含多个非线性隐藏层，这使得它们有强大的表现力，可以学习输入和输出之间非常复杂的关系。但是在训练数据有限的情况下，深度神经网络很容易过度学习造成过拟合，过拟合是深度神经网络的一个非常严重的问题，此外，神经网络越大，训练速度越慢，Dropout可以通过在训练神经网络期间随机丢弃单元来防止过拟合，实验证明Dropout有很好的效果。

一、DropOut简介

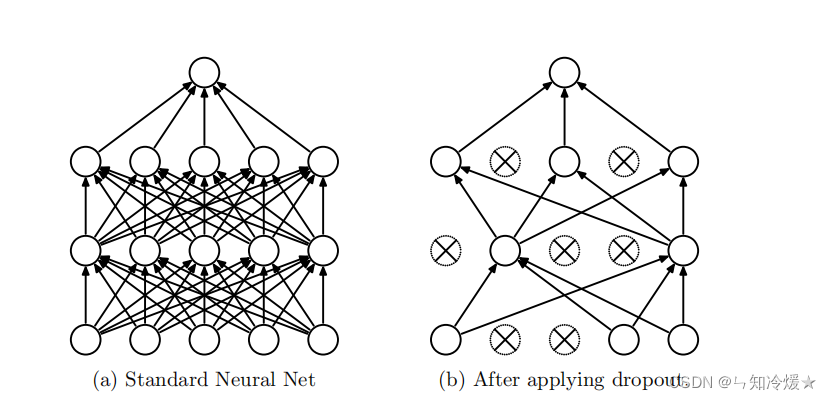
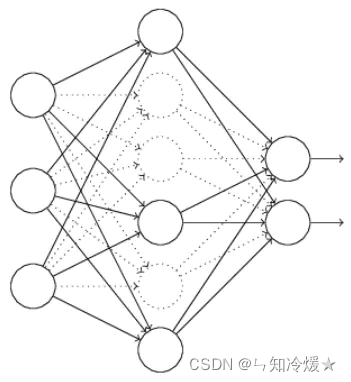
1-1、DropOut论文图解

左图：拥有两层隐藏层的正常神经网络。
右图：应用Dropout后的神经网络。（来源于官方论文）
在这里插入图片描述

1-2、DropOut介绍

DropOut：正常神经网络需要对每一个节点进行学习，而添加了DropOut的神经网络通过删除部分单元（随机），即暂时将其从网络中移除，以及它的所有传入和传出连接。将DropOut应用于神经网络相当于从神经网络中采样了一个“更薄的”网络，即单元个数较少。（如上图所示，DropOut是从左图采样了一个更薄的网络，如图右）在正反向传播的过程中，采样了多个稀薄网络，即Dropout可以解释为模型平均的一种形式。

1-3、DropOut产生动机

产生DropOut的动机：使用DropOut训练的神经网络中的每个隐藏单元必须学会与随机选择的其他单元样本一起工作，这样会使得每个隐藏单元更加的健壮，并使得他们尽量自己可以创造有用的功能，而不是依赖其他隐藏单元。即按照论文的话来说：减少神经元之间复杂的共适应关系。

官方论文例子： 50个人，分十个组，每五个人完成一个小阴谋，可能比50个人正确扮演各自角色完成一个大的阴谋更容易，当然，在时间足够，各种条件没有改变的情况下，那么完成一个大阴谋是更适合的，但生活总是充满变数，大阴谋往往不太容易实现，这样小的阴谋发挥作用的机会就会更大。同样的，在训练集上，各个隐藏单元可以协同发挥作用，即可以在训练集上可以训练的很好，但是这并不是我们需要的，我们需要他们在新的测试集上可以很好的合作，这时候DropOut体现出了它的价值！

本质上看： DropOut通过使其它隐藏层神经网络单元不可靠从而阻止了共适应的发生。因此，一个隐藏层神经元不能依赖其它特定神经元去纠正其错误。因为dropout程序导致两个神经元不一定每次都在一个dropout网络中出现。这样权值的更新不再依赖于有固定关系的隐含节点的共同作用，阻止了某些特征仅仅在其它特定特征下才有效果的情况。迫使网络去学习更加鲁棒的特征，这些特征在其它的神经元的随机子集中也存在。

1-4、DropOut流程简介

简介： 在神经网络的训练过程中，对于一次迭代中的某一层神经网络，先随机选择其中的一些神经元并将其临时丢弃，然后再进行本次的训练和优化。在下一次迭代中，继续随机隐藏一些神经元，直至训练结束。由于是随机丢弃，故而每一个批次都在训练不同的网络。
详细流程：

首先随机（临时）删掉网络中一半的隐藏神经元（以dropout rate为0.5为例），输入输出神经元保持不变。
然后把输入x 通过修改后的网络前向传播，然后把得到的损失结果通过修改的网络反向传播。一小批（这里的批次batch_size由自己设定）训练样本执行完这个过程后，在没有被删除的神经元上按照随机梯度下降法更新对应的参数（w，b）
重复以下过程：
1、恢复被删掉的神经元（此时被删除的神经元保持原样，而没有被删除的神经元已经有所更新），因此每一个mini- batch都在训练不同的网络。
2、从隐藏层神经元中随机选择一个一半大小的子集临时删除掉（备份被删除神经元的参数）。
3、对一小批训练样本，先前向传播然后反向传播损失并根据随机梯度下降法更新参数（w，b）（没有被删除的那一部分参数得到更新，删除的神经元参数保持被删除前的结果）。

二、模型描述

2-1、公式描述

前提：带有L层隐藏层的神经网络。

l：第几层。
z：代表输入向量
y：代表输出向量
W：代表权重
b：偏差
f：激活函数

没有DropOut的神经网络前向传播计算公式可以被描述为：l+1层的输入向量是l+1的权重乘以l层的输出向量加l+1层的偏差。l+1层的输出向量为经过激活函数的l+1层的输入向量。
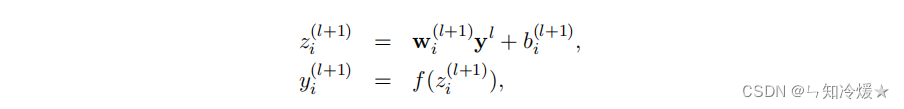
在这里插入图片描述
添加DropOut的神经网络前向传播计算公式可以被描述为：相比于之前输出向量经过了伯努利分布，类似于经过一个门筛选了一下。*代表的是点积。

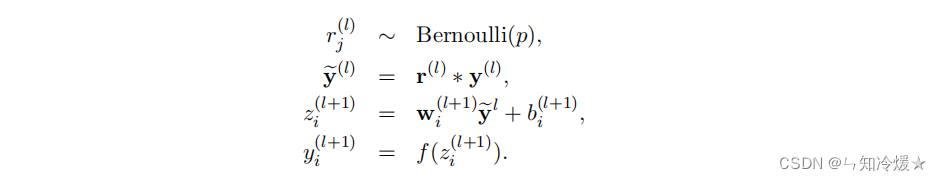
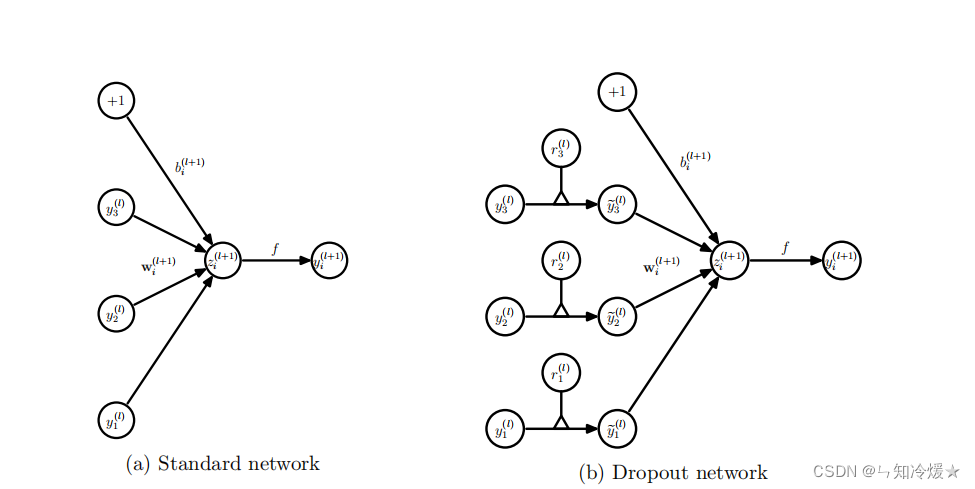
2-2、神经网络图描述

神经网络图示如下所示：左图为标准的神经网络，右图为添加了Dropout的神经网络，相比于标准的神经网络，添加了Dropout的神经网络相当于为前一层的输出向量添加了一道概率流程，即是否经过筛选。
在这里插入图片描述

2-3、一些需要注意的问题！

注意：

在测试中，权重参数w被缩放 $W^l=pW^l$
训练的过程中，会停止训练一些神经元，但是在测试的时候，整个模型是完整的，为了解决这个问题，我们会对没有被dropout的神经元权值做一个rescale，举个栗子：dropout rate为0.5，经过该算式之后rescale rate比例为2，即翻倍，这在一定程度上弥补了删掉一些神经元带来的误差。 $resc a l er a t e = 1/ (1 - d ro p o u t r a t e)$
拓展延伸：如果不想测试阶段缩放权重，可以选择在训练阶段缩放激活函数，即反向Dropout，这样的话在测试阶段可以保持网络不变。所以我们换一个思路，在训练时候将剩余权重乘以1/(1-p)，在测试时，就不需要做什么了。

三、Dropout代码实现以及相关变种（部分有实现）

3-1、Dropout实现（Torch实现）

import torch


# 定义dropout
def dropout_test(x, dropout):
    """
	:param x: input tensor
	:param dropout: probability for dropout
	:return: a tensor with masked by dropout
	"""
    # dropout must be between 0 and 1
    # 判断dropout是不是在0到1之间，如果不是的话直接抛出异常。
    assert 0 <= dropout <= 1
    # if dropout is equal to 0;just return self_x
    # 如果dropout为0，则返回原式
    if dropout == 0:
        return x
    # if dropout is equal to 1: put all values to zeros in tensor x
    # 如果dropout为1，则返回和输入形状相同的全0矩阵。
    if dropout == 1:
        return torch.zeros_like(x)
    # torch.rand is for return a tensor filled with values from uniform distribution [0,1)
    # we compare the values with dropout,if values is greater than dropout ,return 1,else 0
    # 生成一个mask矩阵，用来使一部分数据为0。
    mask = (torch.rand(x.shape) > dropout).float()
    # mask times x and give the scale(1-dropout) for the same expectation with before
    # 使用mask来遮掉部分数据，并且缩放剩余权重。
    return mask * x / (1.0 - dropout)


if __name__ == '__main__':
    # dropout_test
    input = torch.rand(3, 4)
    dropout = 0.8
    output = dropout_test(input, dropout)

    print(f"input={input}")
    print(f"output={output}")

输出：
input=tensor([[0.9379, 0.6264, 0.2145, 0.8403],
[0.6710, 0.7660, 0.0424, 0.2627],
[0.5760, 0.1775, 0.3744, 0.3073]])
output=tensor([[0.0000, 0.0000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.2121, 0.0000],
[0.0000, 0.8876, 0.0000, 0.0000]])

3-2、Dropout实现（Numpy实现，训练集乘以1/(1-p)，测试集不做变化）

在这里插入图片描述

import numpy as np

def another_train(rate, x, w1, b1, w2, b2):
	layer1 = np.maximum(0, (np.dot(x, w1) + b1))
	mask1 = np.random.binomial(1, 1.0 - rate, layer1.shape)
	layer1 = layer1 * mask1
	layer1 = layer1 / (1.0 - rate)
	
	layer2 = np.maximum(0, (np.dot(layer1, w2) + b2))
	mask2 = np.random.binomial(1, 1.0 - rate, layer2.shape)
	layer2 = layer2 * mask2
	layer2 = layer2 / (1.0 - rate)

	return layer2


def another_test(x, w1, b1, w2, b2):
	layer1 = np.maximum(0, np.dot(x, w1) + b1)
	layer2 = np.maximum(0, np.dot(layer1, w2) + b2)
	return layer2

3-3、Dropout实现（Numpy实现，测试集变化）

在这里插入图片描述

import numpy as np

def train(rate, x, w1, b1, w2, b2):
	"""
	description:
	if the train cannot use scale(1/(1-rate)) for output;
	then we need mutiply by (1.0-rate) for keeping the same expectation
	:param rate: probability of dropout
	:param x: input tensor
	:param w1: weight_1 of layer1
	:param b1: bias_1 of layer1
	:param w2: weight_2 of layer2
	:param b2: bias_2 of layer2
	:return: layer2
	"""
	layer1 = np.maximum(0, (np.dot(x, w1) + b1))
	mask1 = np.random.binomial(1, 1.0 - rate, layer1.shape)
	layer1 = layer1 * mask1

	layer2 = np.maximum(0, (np.dot(layer1, w2) + b2))
	mask2 = np.random.binomial(1, 1.0 - rate, layer2.shape)
	layer2 = layer2 * mask2
	return layer2


def test(rate, x, w1, b1, w2, b2):
	layer1 = np.maximum(0, np.dot(x, w1) + b1)
	layer1 = layer1 * (1.0 - rate)

	layer2 = np.maximum(0, np.dot(layer1, w2) + b2)
	layer2 = layer2 * (1.0 - rate)

	return layer2

3-4、Dropout实现（复写一个类似于Pytorch中的Dropout）

# nn.Module，继承自nn.Module。
class Dropout(nn.Module):
    def __init__(self, p=0.5):
        super(Dropout, self).__init__()
        if p <= 0 or p >= 1:
            raise Exception("p value should accomplish 0 < p < 1")
        self.p = p
        self.kp = 1 - p
        
    def forward(self, x):
        if self.training:
        	# 生成mask矩阵。
        	# torch.rand_like：生成和x相同尺寸的张量，取值在[0,1)之间均匀分布。
            mask = (torch.rand_like(x) < self.kp)
            # 先用mask矩阵对x矩阵进行处理，再除以1 - p（保留概率），即上述所说的反向DropOut操作，不需要在测试集上再缩放。
            return x * mask / self.kp
        else:
            return x

3-5、高斯Dropout

高斯Dropout: 在高斯Dropout中，每个节点可以看做乘以了p(1-p) ，所有节点都参与训练。

class GaussianDropout(nn.Module):
    def __init__(self, p=0.5):
        super(GaussianDropout, self).__init__()
        if p <= 0 or p >= 1:
            raise Exception("p value should accomplish 0 < p < 1")
        self.p = p
        
    def forward(self, x):
        if self.training:
        	# 式子算起来有些许区别。
            stddev = (self.p / (1.0 - self.p))**0.5
            epsilon = torch.randn_like(x) * stddev
            return x * epsilon
        else:
            return x

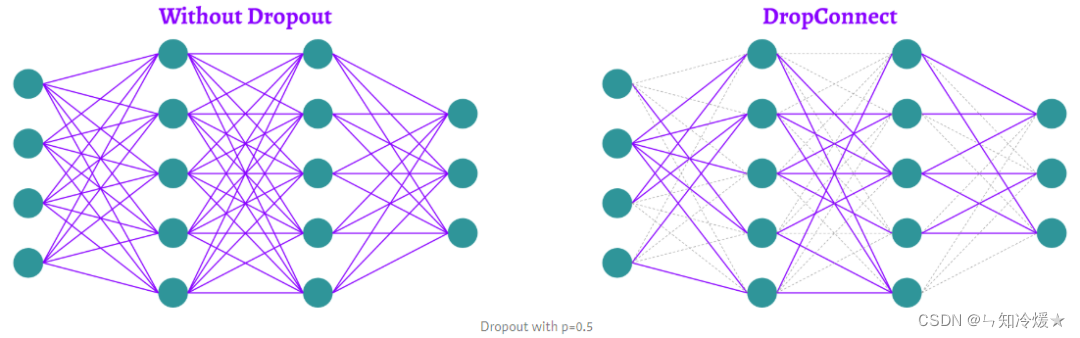
3-6、DropConnect

本质：不直接在神经元上应用dropout，而是应用在连接这些神经元的权重和偏置上。

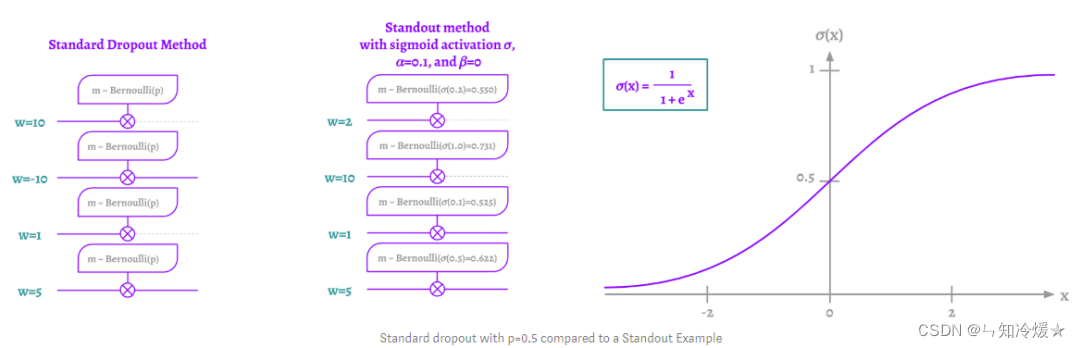
在这里插入图片描述

3-7、Standout

本质：神经元被遗漏的概率p在这一层并不是固定的，根据权重的值，它是自适应的。
在这里插入图片描述

附录1、nn.Linear()详解

nn.Linear()：用于设置网络中的全连接层。

参数：
in_features：输入的二维张量的大小，即输入的[batch_size, size]中的size。例如Mnist数据集中，输入维度为[batch, 1, 28, 28],则size为12828，即真实输入我们首先需要转化为二维张量[batch, 12828]，之后再输入。
out_features：输出二维张量的大小，输出二维张量的形状为[batch_size, output_size]。

总结：相当于一个输入为[batch_size, in_features]的张量变换成了[batch_size, out_features]的输出张量。

import torch as t
from torch import nn

# in_features由输入张量的形状决定，out_features则决定了输出张量的形状 
connected_layer = nn.Linear(in_features = 3*64*64, out_features = 1)

# 假定输入的图像形状为[3,64,64]
input = t.randn(1,3,64,64)

# 将四维张量转换为二维张量之后，才能作为全连接层的输入
input = input.view(1,3*64*64)
print(input.shape)
output = connected_layer(input) # 调用全连接层
print(output.shape)

输出：
torch.Size([1, 12288])
torch.Size([1, 1])

参考文章：
Dropout详解.
一文看尽12种Dropout及其变体.
dropout代码实现学习笔记.

Dropout、高斯Dropout、均匀分布Dropout（Uout）.
15 - Dropout的原理及其在TF/PyTorch/Numpy的源码实现.
伯努利分布——百度百科.
理解dropout.
CNN 入门讲解：什么是dropout?.
Dropout作用原理.
Dropout原理与实现.
PyTorch的nn.Linear（）详解.