目录

2.3 Limitations of Perfect Secrecy 完美保密性的局限性

THEOREM 2.11 完美保密对密钥空间的要求

THEOREM 2.11 的证明

---

2.3 Limitations of Perfect Secrecy 完美保密性的局限性

在前一节的最后，我们指出了一次性密码本方案的缺点。事实上，这些缺点并不是特定于该方案的，而是保密完善性的固有限制。具体地说，我们证明了任何完全保密的加密方案都必须有一个至少与消息空间一样大的密钥空间。

---

THEOREM 2.11 完美保密对密钥空间的要求

If (Gen, Enc, Dec) is a perfectly secret encryption scheme with message space M and key space K, then |K| ≥ |M|.

如果一个在明文空间 M 且密钥空间K的加密方案Π(Gen, Enc, Dec)是完美保密的，则|K| ≥ |M|

---

THEOREM 2.11 的证明

我们使用反证法，即假设某加密方案的|K|＜|M|，然后证明此方案不满足完美保密

我们假设|K|＜|M|。考虑M上的均匀分布，设c∈C是一个以非零概率产生的密文。设M (c)是所有由c解密得到的消息的集合

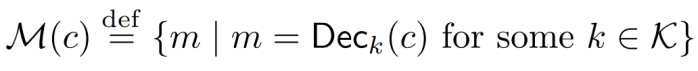
显然|M(c)| ≤ |K|。根据假设的|K|＜|M|，我们将得到|M(c)|＜|M|

这意味着存在m’∈M，使得m’ ∉M (c)，则

Pr[M = m’ | C = c] = 0 ≠ Pr[M = m’ ]

这与保密完备性的要求相违背，假设不成立