求圆心到点的直线与圆的相交点

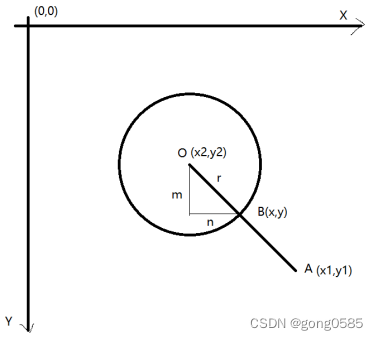
点B为圆上一动点，已知圆心O(x2,y2), 圆外点A(x1,y1)，圆半径r值，求B(x,y)坐标。

由图可知,产生下面两个公式。

m/n = y1-y2/x1-x2

m^2+n^2=r^2

由上面的公式可以得出

n的长度计算公式为n^2= r^2 / [ (y1-y2 / x1-x2)^2 + 1]

点B的坐标为(x2-n, y2+m)

PolygonUtils.java代码如下：

public class PolygonUtils {

/**
   * 求交点坐标
   * @param p1 圆外任意一点坐标
   * @param o1 圆心坐标
   * @param radius 圆半径
   * @return
   */

    public PointDto getLine4CircularV1(PointDto p1, PointDto o1, double radius){
        //m，n分别为为交点跟圆心在y轴，和x轴的间距;
        double m=0,n=0;
        double y = p1.y-o1.y, x = p1.x-o1.x;
        //计算m和n
        //n^2= r^2 / [ (y1-y2 / x1-x2)^2 + 1]
        n = pow(radius, 2) / (pow(y / x, 2) + 1) ;
        //m^2 + n^2 = r^2
        m = sqrt( pow(radius, 2) - n);
        n = sqrt(n);
        PointDto dto = new PointDto();
        if(x > 0){
            if(y > 0){
               //在第四象限
            }else{
                //在第一象限
                m *= -1;
            }
        }else{
            n *= -1;
            if(y > 0){
                //在第三象限
            }else{
                //在第二象限
                m *=-1;
            }
        }
        dto.setY(o1.y+ m);
        dto.setX(o1.x+ n);
        return dto;
    }
}

PointDto.java

public class PointDto {
    public double x;
    public double y;

    public PointDto() {
        super();
    }
    public PointDto(double x, double y) {
        this.x = x;
        this.y = y;
    }

    public double getX() {
        return x;
    }

    public void setX(double x) {
        this.x = x;
    }

    public double getY() {
        return y;
    }

    public void setY(double y) {
        this.y = y;
    }
}