堆
- 1.堆:一种二叉树
- 2.堆的概念及结构
- 3.堆的实现
- 3.1 创建堆的结构
- 3.2 堆的初始化
- 3.3 堆的插入
- 3.4 堆的向上调整法(up)
- 3.5 打印堆的数据
- 3.6 到这里就可以实现一个基本的堆了
- 3.7 向下调整法down(非常重要的一个方法)
- 3.8 最优的建堆算法
- 3.8.1 建堆算法时间复杂度分析
- 3.9堆的一些操作(pop,top,size,empty)
- 3.9.1 堆的删除 pop
- 3.9.2 取堆顶元素
- 3.9.2 堆的大小
- 3.9.3 判断堆是否为空
- 3.10 堆的销毁
- 4.总结
1.堆:一种二叉树
堆是一种完全二叉树,使用顺序结构的数组来存储。
不了解完全二叉树的小伙伴可以看看这篇文章,这里不再赘述
二叉树
使用完全二叉树可以避免空间的浪费,因为完全二叉树结点之间从逻辑图看一定是连续的
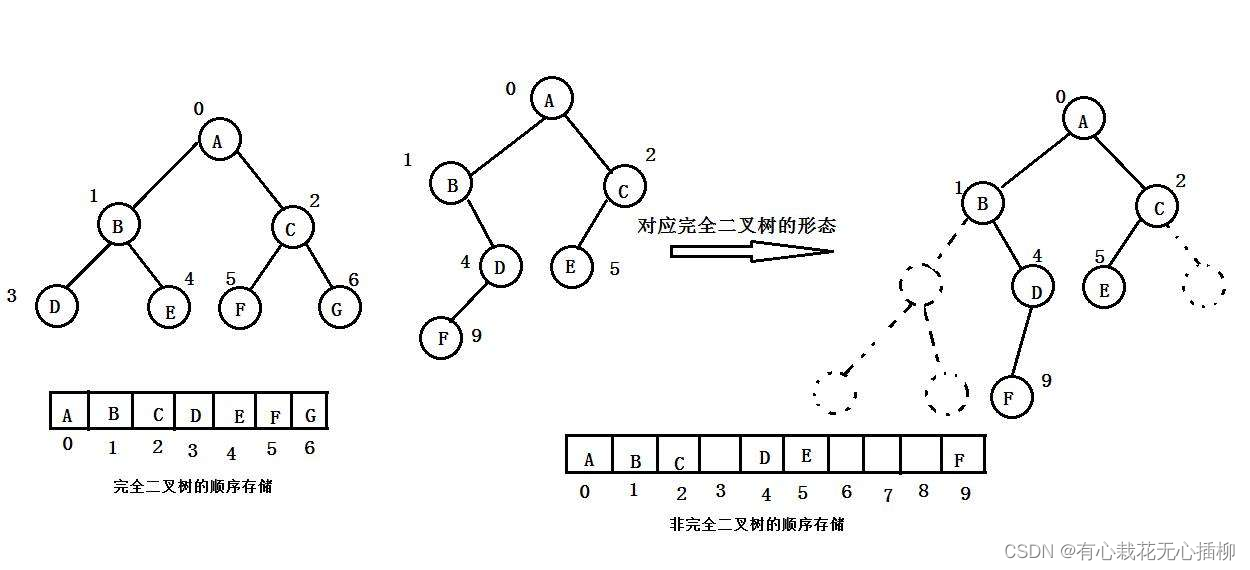
我们要做的是像最左边的逻辑图那样利用顺序结构实现堆
需要注意的是这里的堆和操作系统虚拟进程地址空间中的堆是两回事,一个是数据结构,一个是操作系统中管理内存的一块区域分段。
2.堆的概念及结构

堆的性质:
1.堆中某个结点的值总是不大于或不小于父节点的值
2.堆总是一棵完全二叉树
如图所示
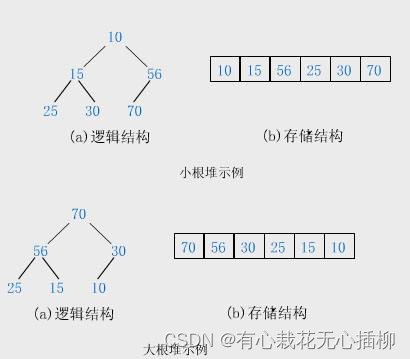
3.堆的实现
3.1 创建堆的结构
typedef int data_type; //把int typedef这样可以方便以后随时更换数据类型
typedef struct heap // 这里默认是大根堆
{
int* a; // 数组模拟堆
int size; // 元素数量
int capacity; // 堆的当前容量
}heap;
3.2 堆的初始化
void init(heap* h)
{
assert(h); //断言一下,防止传入空
h->a = NULL;
h->size = 0;
h->capacity = 4; // 容量初始化为 4
int* tmp = (heap*)malloc(sizeof(heap) * h -> capacity);
//malloc动态开辟数组大小
if (tmp == NULL) //养成好习惯,malloc后判断是否开辟成功
{
perror("malloc");
exit(-1);
}
h->a = tmp; // 开辟成功后,再把开辟的空间给我们的堆的数组
}
3.3 堆的插入
我们要往堆里面插入数据,最好的方法就是在数组的末尾插入,因为如果在数组前面插入的话,整个数组的其他元素还要往后挪,在中间插入也要挪,最好的方法就是往末尾插入,再去调整它,保持大根堆或者小根堆,我们这里默认实现大根堆。
void push(heap* h, data_type x) // x 是我们要插入的数据
{
assert(h);
if (h -> size == h->capacity) //判断容量是否满了,满了就扩容
{
int* tmp = (heap*)realloc(h->a, sizeof(heap) * h->capacity * 2);//每次扩两倍
if (tmp == NULL) //养成好习惯判断是否扩容成功
{
perror("malloc");
exit(-1);
}
h->a = tmp; // 扩容成功再赋给堆的数组a
h->capacity *= 2; //别忘了我们的结构体成员变量也要 *2
}
h->a[h->size] = x; //往size的位置插入x,每次都在末尾插入
h->size++;//插入后每次size++,方便下次插入
up(h -> a, h -> size - 1); // 然后使用向上调整法,我们下面讲
//每插入一个数据就利用向上调整
}
3.4 堆的向上调整法(up)
向上调整法就是找到一个结点,然后拿这个结点与它的父亲去比较,
如果我们想实现大根堆,就判断这个结点是否比它的父亲大,满足条件就和这个的结点的父亲交换。
然后一直向上做判断,交换,做判断,交换。知道走到最顶层为止。
时间复杂度为 O(log2 n)
void up(data_type* a,int child)
{
int parent = (child - 1) / 2; //利用孩子结点找父亲结点公式
while (child > 0) // 走到最顶层为止
{
if (a[child] > a[parent])//如果孩子结点大于父亲
{
swap(&(a[child]), &(a[parent]));//交换
child = parent; //把父亲结点变换成孩子结点,继续向上做判断,交换
parent = (child - 1) / 2;//再一次找新孩子的父亲
}
else //如果孩子结点小于父亲,就不满足条件,break这次循环
{
break;
}
}
}
代码里的swap函数
void swap(data_type * n1, data_type* n2)
{
int tmp = *n1;
*n1 = *n2;
*n2 = tmp;
}
3.5 打印堆的数据
我们先实现堆的打印,然后就可以查看堆里的数据了。
void print(heap* h)
{
assert(h);
for (int i = 0; i < h->size; i++)
{
printf("%d ", h->a[i]);
}
printf("\n");
}
3.6 到这里就可以实现一个基本的堆了
void test1() // 测试
{
heap h1;
init(&h1);
push(&h1, 50);
push(&h1, 25);
push(&h1, 90);
push(&h1, 33);
push(&h1, 12);
print(&h1); // 结果是 90 33 50 25 12
//可以手动按顺序画个逻辑图,会发现确实是大根堆
}
我们模拟一下这个过程
一开始插入50,h1->a[0] = 50,h1 -> size++ ,此时size = 1
然后每插入一个数向上调整
up(h1->a,h1->size - 1 ) size - 1 是因为前面提前加了1
因为一开始只有一个数,所以up函数实际没用。
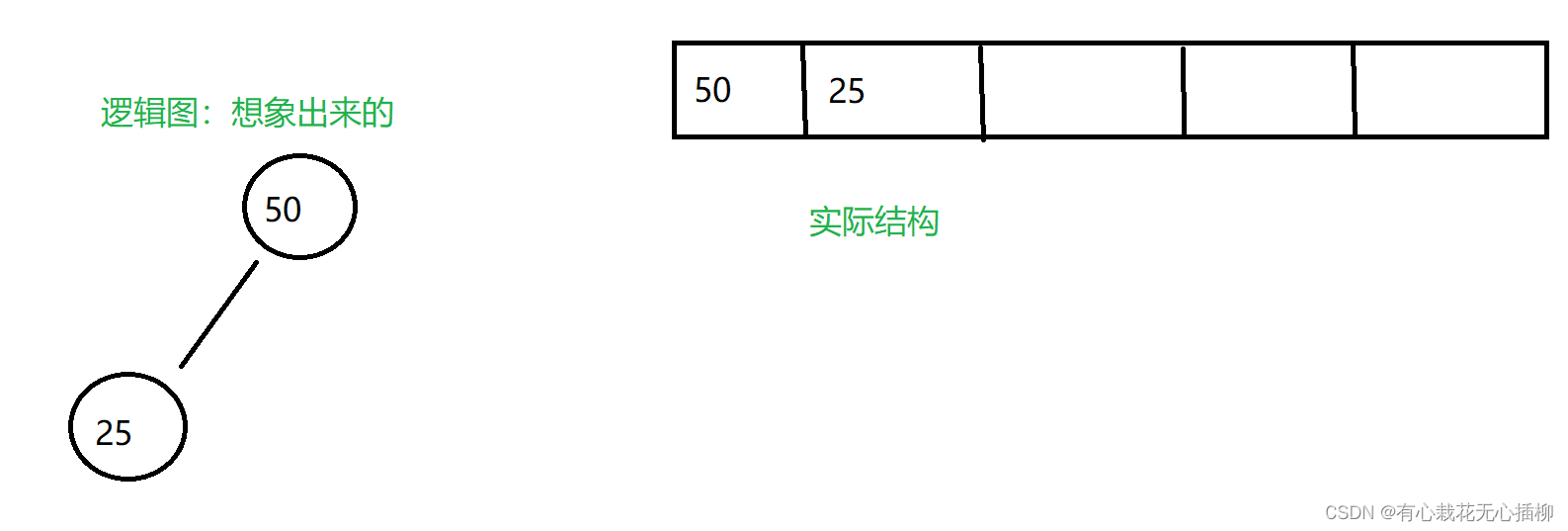
插入25后,调用up,发现25 < 50, 我们这里实现的是大根堆,所以不做交换。
接下来插入 90
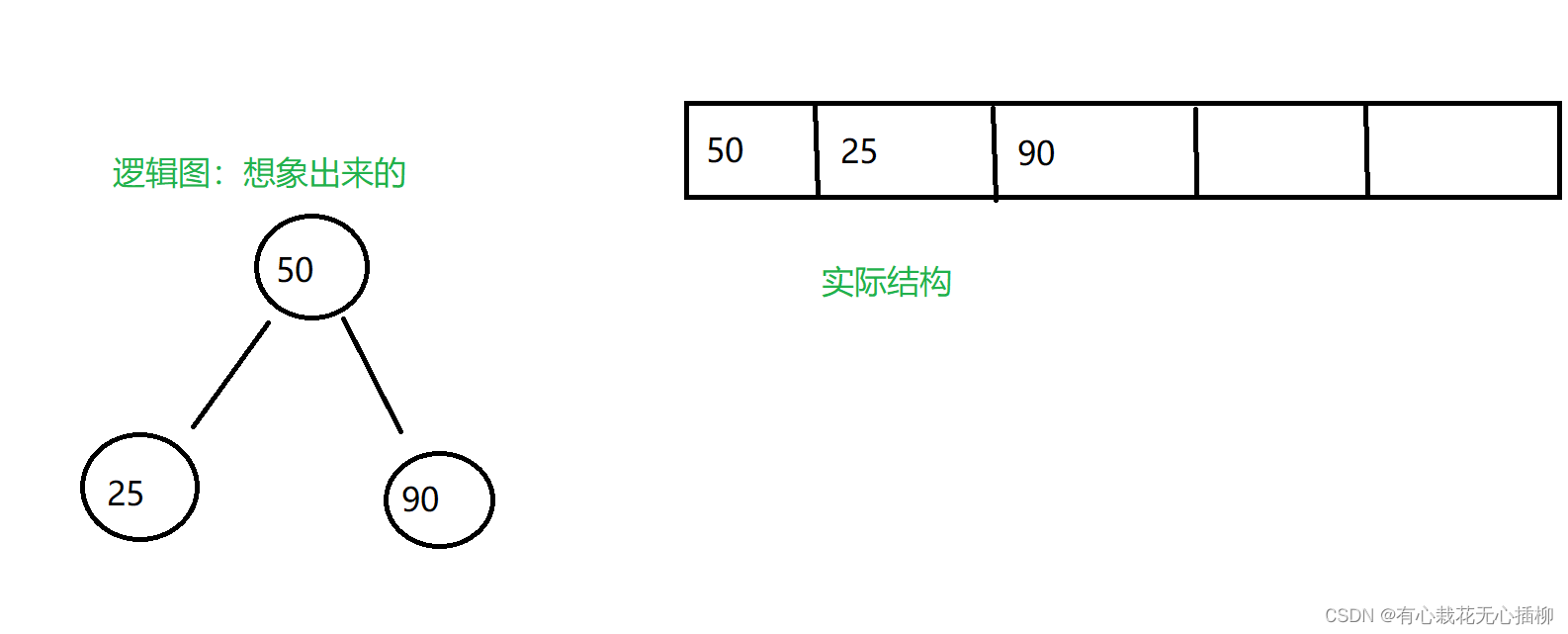
调用一次up ,发现这个结点大于我的父结点,交换。
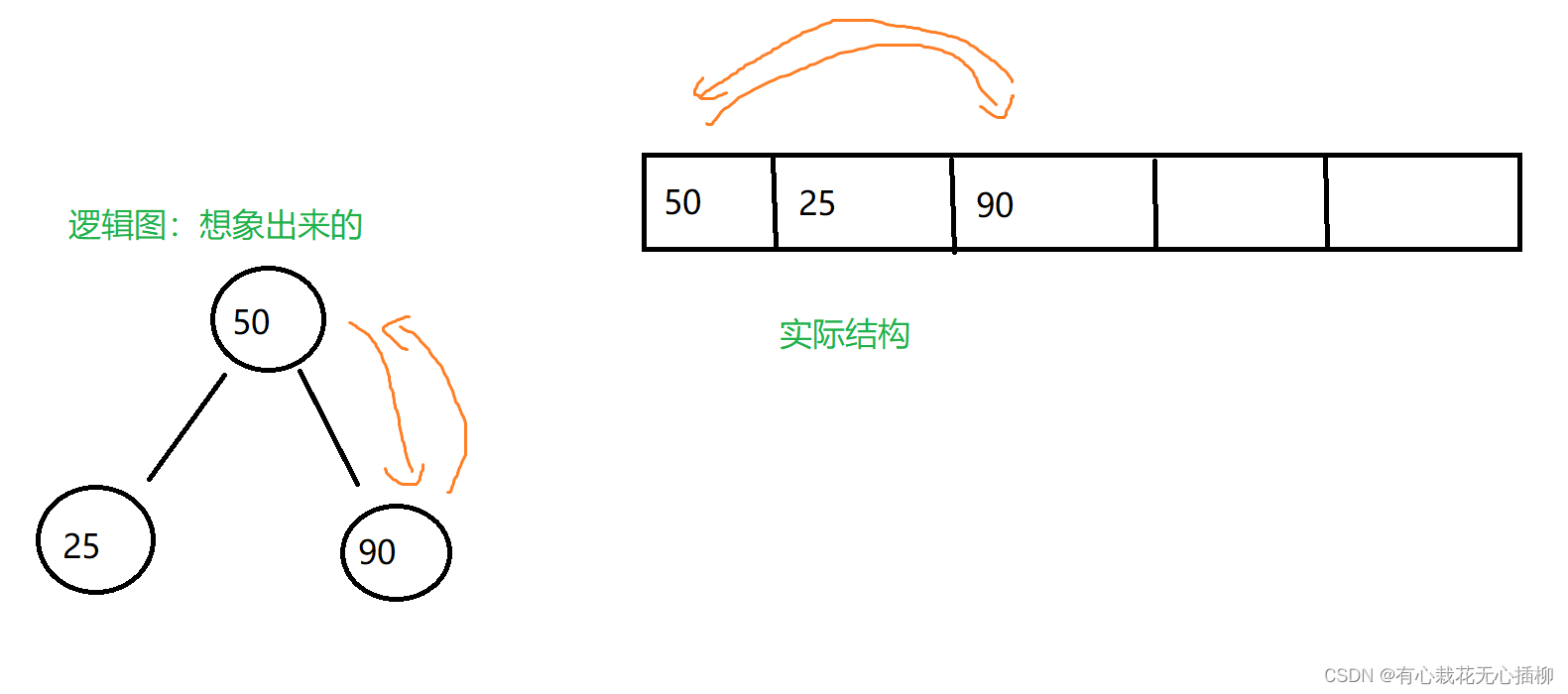
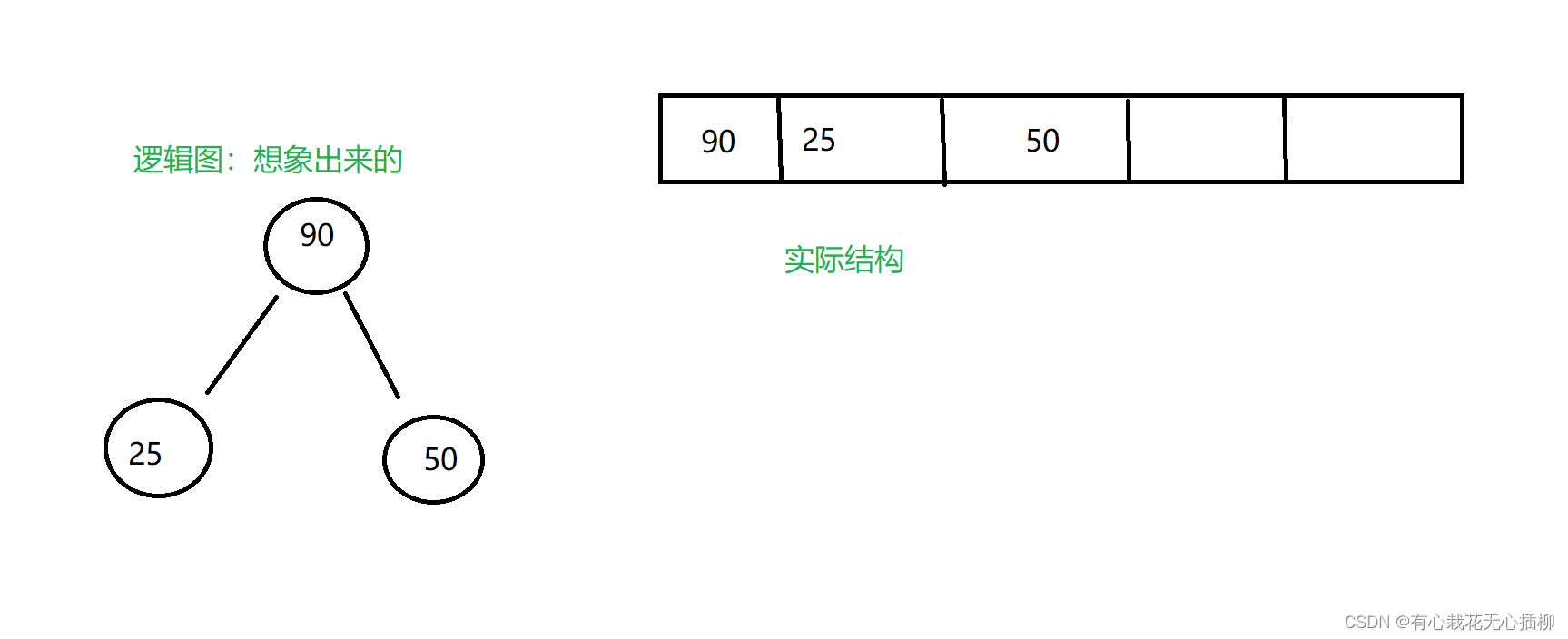
剩下的数据同理,大家可以自行模拟感受一下。
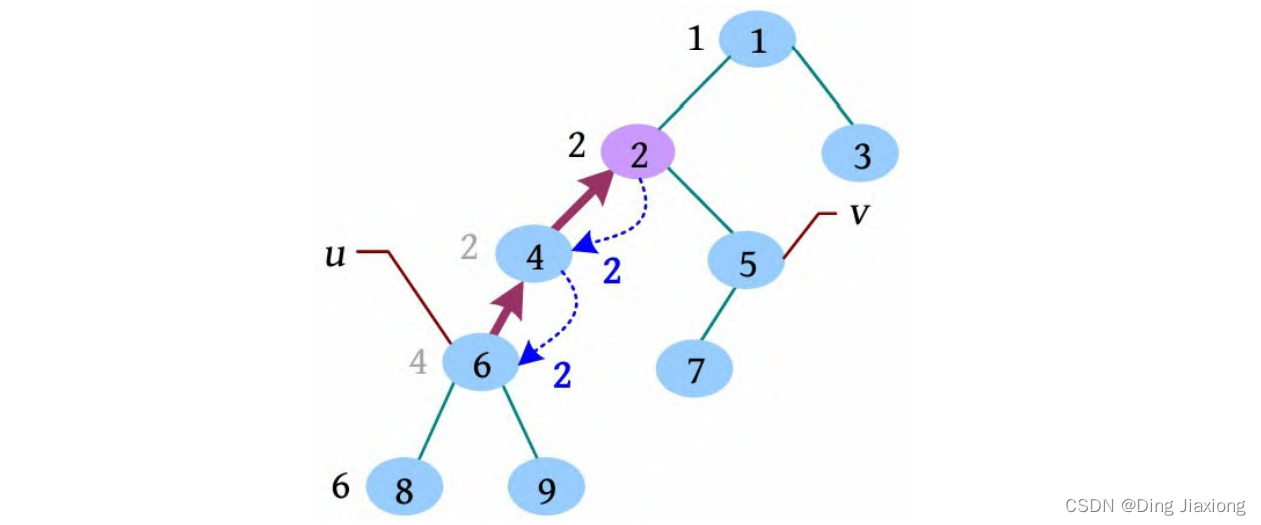
3.7 向下调整法down(非常重要的一个方法)
向下调整法就是找到该节点的孩子,判断我的两个孩子谁比我大或者谁比我小,实现大根堆或者小根堆。
比如我们想实现大根堆,我们找到一个结点的两个左右孩子,如果孩子比父亲大,就交换。
注意,这里可以两个孩子都比父结点大,所以我们要找到最大的孩子交换。
然后一直往下判断,交换,判断,交换,达到最底层为止。
已知根结点求孩子的方法
left_child = (parent * 2) + 1 //左孩子
right_child = (parent * 2) + 2// 右孩子
向下调整法代码如下:
void down(data_type* a, int len, int parent)
{
int child = (parent * 2) + 1; // 先假设左孩子最大
while (child < len) //直到达到最底层就停止
{
//这里加1可能会有越界问题,可能会访问到随机值,导致出错,判断一下
if (child + 1 < len && a[child + 1] > a[child]) // 如果右孩子大的话就 child++
{
child++;
}
if (a[parent] < a[child])//如果父结点小于孩子结点就交换
{
swap(&a[parent], &a[child]);
parent = child;
child = (parent * 2) + 1;
}
else
{
break;//否则break
}
}
}
3.8 最优的建堆算法
向下调整法是 建堆算法一个非常重要的算法。
注意这里的建堆不同于上面的插入建堆,而是随便给你一个数组,要求你在最优的时间复杂度,把这个数组建立成堆,也就是大根堆或者小根堆。
如果我们一个一个插入去实现,时间复杂度就是O(n * log2n)
或者利用向上调整法,从第二层开始逐层向上调整,时间复杂度也是O(n* log2n)
而如果利用我们的向下调整法,从倒数第二层开始向下调整,然后倒数第三层向下调整,直到最顶层,是可以做到时间复杂度为O(n)的。
最简单的一个优化理解就是,二叉树中一般最后一层占的结点最多,一般占了总结点的一半以上,我们直接省去了最后一层的计算,所以优化成了O(n)
void creat_heap(heap* h, data_type *arr, int n) //建堆算法:从倒数第二层开始向下调整
{//这里的建堆是指传入一个数组,把它建成大堆或者小堆
//时间复杂度O(n)
assert(h);
//malloc一个堆的新数组
h->a = (heap*)malloc(sizeof(heap) * n);
if (h -> a == NULL)
{
perror("malloc:");
exit(-1);
}
//把原来数组的内容复制到新数组
memcpy(h -> a, arr, sizeof(data_type) * n);
h->size = h->capacity = n;//大小和容量也给过去
for (int i = (n - 1 - 1) / 2; i >= 0; i--)
{
// (n - 1 - 1) / 2 求倒数第一个非叶结点的位置
//从倒数的第一个非叶子节点的子树开始调整
down(h -> a, n, i);
}
}
3.8.1 建堆算法时间复杂度分析
void test2()
{
heap h2;
int arr[] = { 1,5,3,8,7,6 };
int n = sizeof(arr) / sizeof(arr[0]);
creat_heap(&h2, arr,n);
print(&h2); // 8 7 6 5 1 3
}
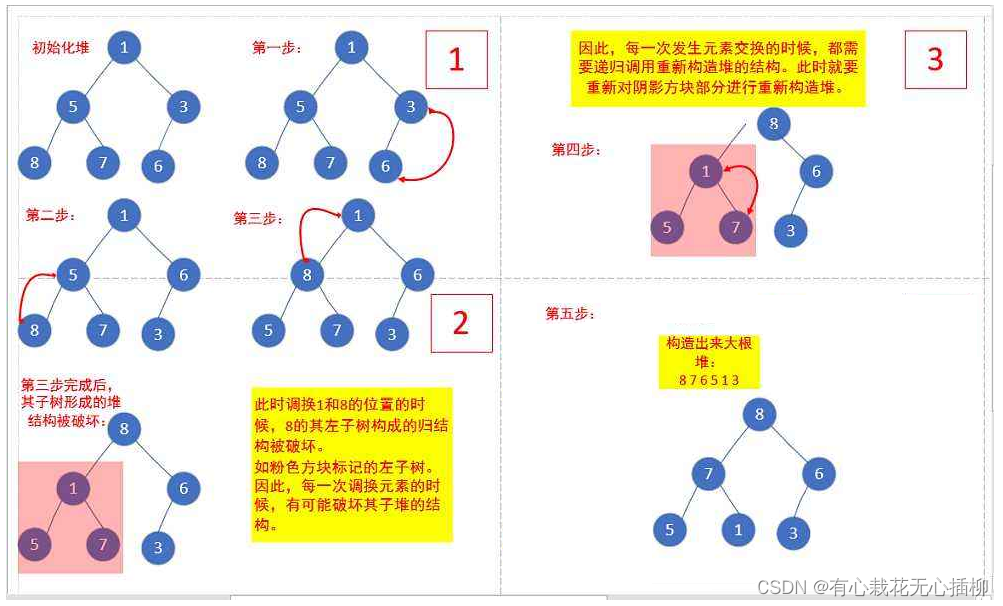
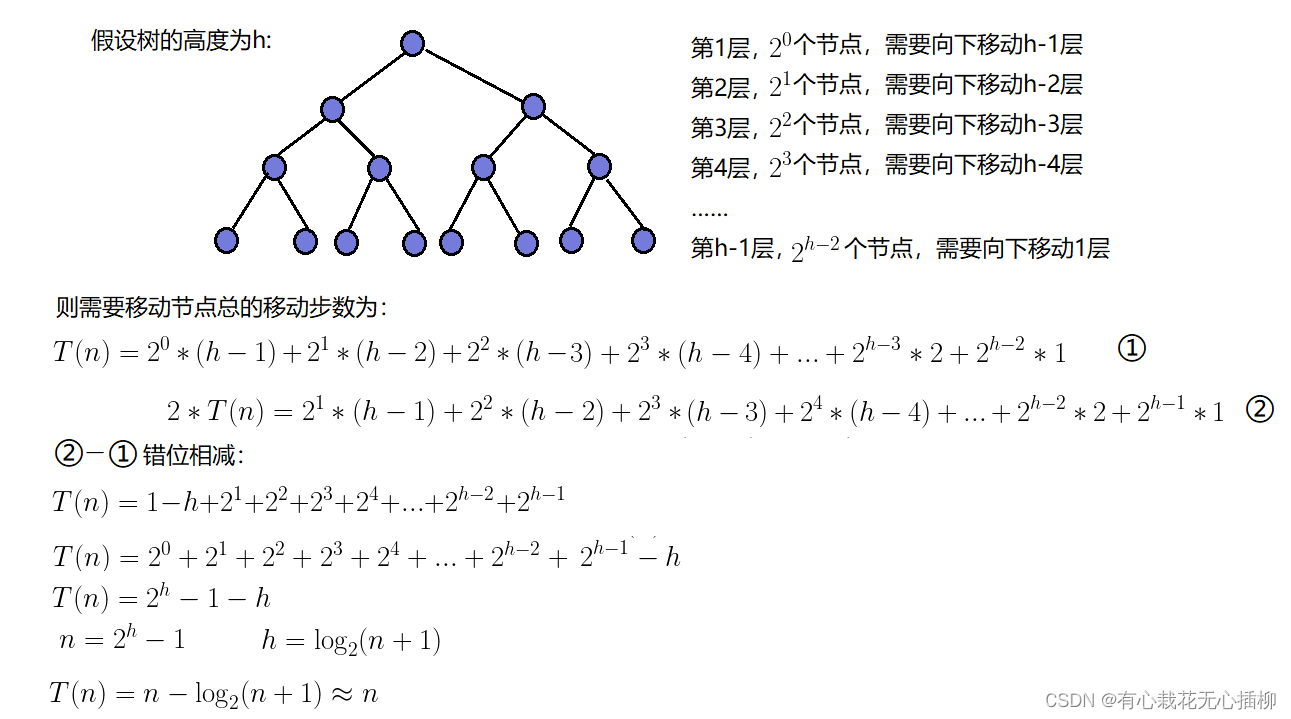
其实最简单的理解方式还是上面说的,最后一层的结点几乎占了总结点的一半,我们的向下调整法从倒数第一个非叶子开始,就省去了最后一层结点的计算,所以才能得到优化。
3.9堆的一些操作(pop,top,size,empty)
3.9.1 堆的删除 pop
堆的删除指的是删除堆顶的元素。
如果是直接删除堆顶元素,那我这个数组还要往前挪动,再向下调整
时间复杂度就是
O(n + log2n)
这种方法不怎么好。
我们这里的删除操作是用堆顶元素与堆最后的元素交换,然后size–
交换后,堆顶元素再向下调整,重新调整堆。
时间复杂度为 O(log2n)
void pop(heap* h)
{
assert(h);
assert(h->size > 0);
swap(&h -> a[0], &h -> a[h -> size - 1]);
h->size--;
down(h->a, h->size, 0);
}
3.9.2 取堆顶元素
data_type top(heap* h)
{
assert(h);
return h->a[0];
}
3.9.2 堆的大小
int heap_size(heap* h)
{
assert(h);
return h->size;
}
3.9.3 判断堆是否为空
bool heap_empty(heap* h)
{
assert(h);
return h->size == 0;
}
3.10 堆的销毁
void destroy(heap* h)
{
assert(h);
free(h->a);
h->a = NULL;
h->size = h->capacity = 0;
}
4.总结
以上就是堆的实现
重点是建堆算法
在后续文章中我们会讲到堆排序,和利用堆解决topK问题(前k大或前k小的数)
其实堆在C++中已经实现好了,我们直接用就好了,但是理解底层的实现原理,才能让我们在编程这条路上走的更远。