1、线性回归

参考资料1：https://blog.csdn.net/bit452/article/details/109627469
参考资料2：http://biranda.top/Pytorch%E5%AD%A6%E4%B9%A0%E7%AC%94%E8%AE%B0003%E2%80%94%E2%80%94%E7%BA%BF%E6%80%A7%E6%A8%A1%E5%9E%8B/#%E7%BA%BF%E6%80%A7%E6%A8%A1%E5%9E%8B

1.1 一元线性回归y=wx代码

要求： 实现线性模型（y=wx）并输出loss的图像。
代码：

import numpy as np
import matplotlib.pyplot as plt

x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
#前馈计算
def forward(x):
    return x * w
#求loss
def loss(x, y):
    y_pred = forward(x)
    return (y_pred-y)*(y_pred-y)

w_list = []
mse_list = []
#从0.0一直到4.1以0.1为间隔进行w的取样
for w in np.arange(0.0,4.1,0.1):
    print("w=", w)
    l_sum = 0
    for x_val,y_val in zip(x_data,y_data):
        y_pred_val = forward(x_val)
        loss_val = loss(x_val,y_val)
        l_sum += loss_val
        print('\t',x_val,y_val,y_pred_val,loss_val)
    print("MSE=",l_sum/3)
    w_list.append(w)
    mse_list.append(l_sum/3)

#绘图
plt.plot(w_list,mse_list)
plt.ylabel("Loss")
plt.xlabel('w')
plt.show()

结果：
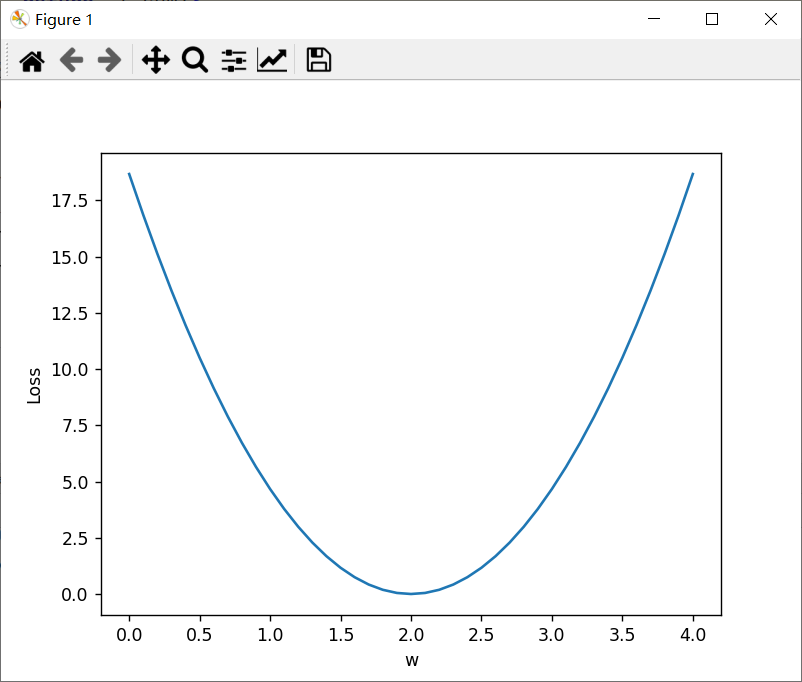
在这里插入图片描述

1.2 一元线性回归y=wx+b代码

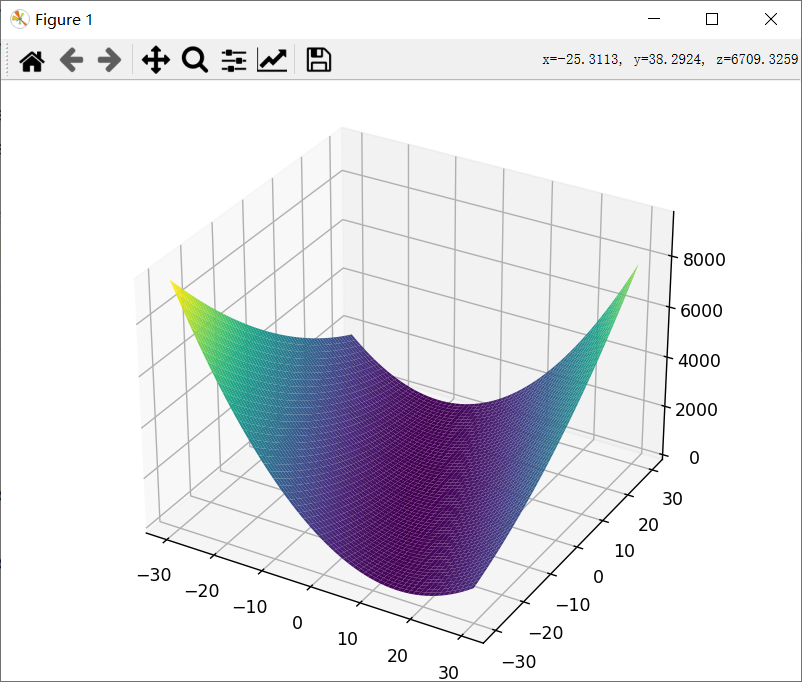
要求： 实现线性模型（y=wx+b）并输出loss的3D图像。
代码：

import numpy as np
import matplotlib.pyplot as plt;
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm

x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]

#线性模型
def forward(x,w,b):
    return x * w+ b

#损失函数
def loss(x, y,w,b):
    y_pred = forward(x,w,b)
    return (y_pred - y) * (y_pred - y)

def mse(w,b):
    l_sum = 0
    for x_val, y_val in zip(x_data, y_data):
        y_pred_val = forward(x_val,w,b)
        loss_val = loss(x_val, y_val,w,b)
        l_sum += loss_val
        print('\t', x_val, y_val, y_pred_val, loss_val)
    print('MSE=', l_sum / 3)
    return  l_sum/3

#迭代取值，计算每个w取值下的x，y，y_pred,loss_val
mse_list = []

##画图
##定义网格化数据
b_list=np.arange(-30,30,0.1)
w_list=np.arange(-30,30,0.1)

##生成网格化数据
xx, yy = np.meshgrid(b_list, w_list,sparse=False, indexing='ij')

##每个点的对应高度
zz=mse(xx,yy)

fig = plt.figure()#定义图像窗口
ax = Axes3D(fig)#在窗口上添加3D坐标轴
ax.plot_surface(xx, yy, zz,rstride=10, cstride=10, cmap=cm.viridis)#生成曲面，cm.viridis是颜色
# rstride（row）指定行的跨度，cstride(column)指定列的跨度
plt.show()

结果：
在这里插入图片描述

2、梯度下降算法

参考资料1：https://blog.csdn.net/bit452/article/details/109637108
参考资料2：http://biranda.top/Pytorch%E5%AD%A6%E4%B9%A0%E7%AC%94%E8%AE%B0004%E2%80%94%E2%80%94%E6%A2%AF%E5%BA%A6%E4%B8%8B%E9%99%8D%E7%AE%97%E6%B3%95/#%E9%97%AE%E9%A2%98%E8%83%8C%E6%99%AF

2.1 梯度下降算法

代码：

import numpy as np
import matplotlib.pyplot as plt

x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
_cost = []
w = 1.0
#前馈计算
def forward(x):
    return x * w
#求MSE
def cost(xs, ys):
    cost = 0
    for x, y in zip(xs,ys):
        y_pred = forward(x)
        cost += (y_pred-y) ** 2
    return cost/len(xs)
#求梯度
def gradient(xs, ys):
    grad = 0
    for x, y in zip(xs,ys):
        temp = forward(x)
        grad += 2*x*(temp-y)
    return grad / len(xs)

for epoch in range(100):
     cost_val = cost(x_data, y_data)
     _cost.append(cost_val)
     grad_val = gradient(x_data, y_data)
     w -= 0.01*grad_val
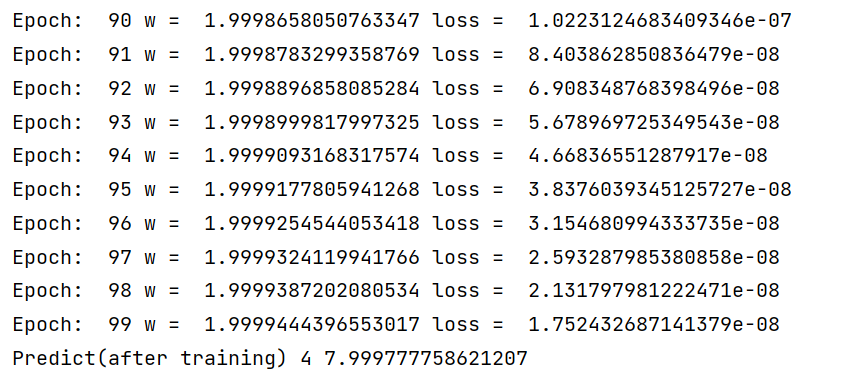
     print("Epoch: ",epoch, "w = ",w ,"loss = ", cost_val)
print("Predict(after training)",4,forward(4))

#绘图
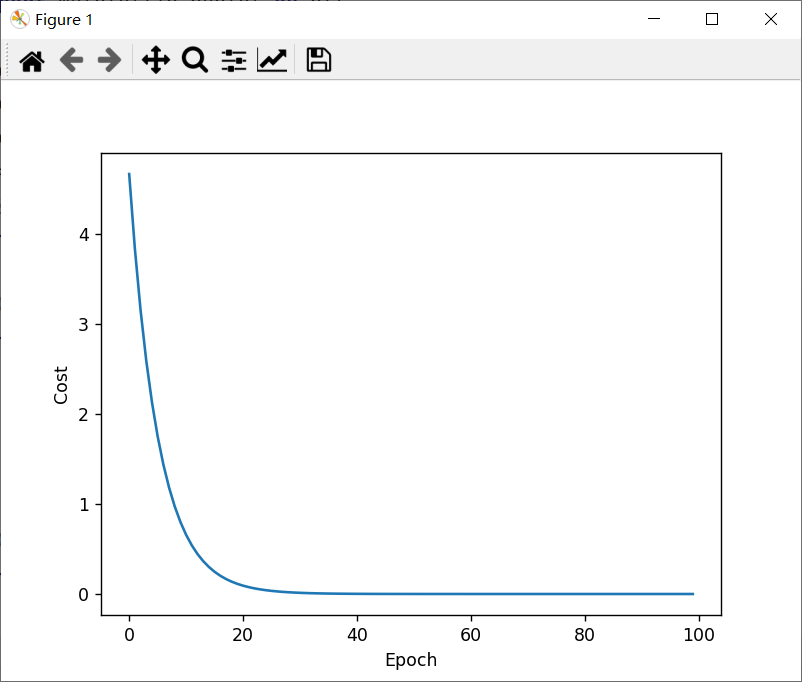
plt.plot(range(100),_cost)
plt.ylabel("Cost")
plt.xlabel('Epoch')

plt.show()

结果：
在这里插入图片描述

2.2 随机梯度下降算法

代码：

#随机梯度下降
import numpy as np
import matplotlib.pyplot as plt

x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
_cost = []
w = 1.0
#前馈计算
def forward(x):
    return x * w
#求单个loss
def loss(x, y):
    y_pred = forward(x)
    return (y_pred-y) ** 2
#求梯度 随机梯度下降的 loss是计算一个训练数据的损失
def gradient(x, y):
    return 2*x*(x*w-y)
print("Predict(after training)",4,forward(4))

for epoch in range(100):
    for x, y in zip(x_data,y_data):
        grad=gradient(x,y)
        w -= 0.01*grad
        print("\tgrad:  ",x,y,grad)
        l = loss(x,y)
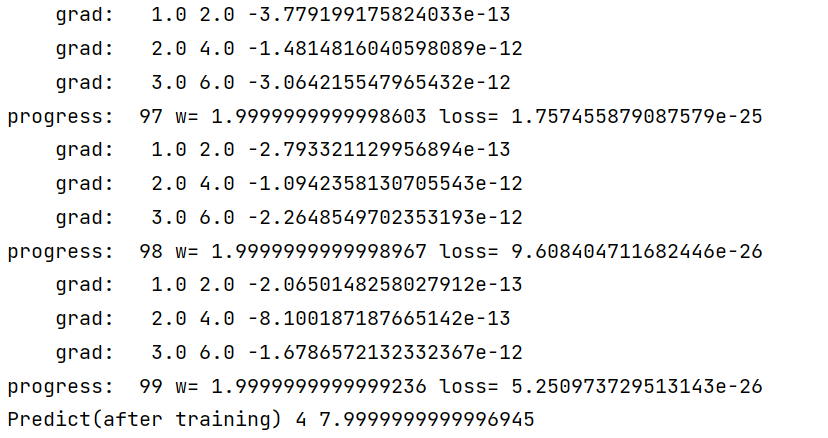
    print("progress: ",epoch,"w=",w,"loss=",l)
print("Predict(after training)",4,forward(4))

结果：
在这里插入图片描述

2.3 区别：

随机梯度下降法和梯度下降法的主要区别在于：

1、损失函数由cost()更改为loss()。cost是计算所有训练数据的损失，loss是计算一个训练数据的损失。对应于源代码则是少了两个for循环。

2、梯度函数gradient()由计算所有训练数据的梯度更改为计算一个训练数据的梯度。

3、本算法中的随机梯度主要是指，每次拿一个训练数据来训练，然后更新梯度参数。本算法中梯度总共更新100(epoch)x3 = 300次。梯度下降法中梯度总共更新100(epoch)次。

3、反向传播

参考资料1：https://blog.csdn.net/bit452/article/details/109643481
参考资料2：http://biranda.top/Pytorch%E5%AD%A6%E4%B9%A0%E7%AC%94%E8%AE%B0005%E2%80%94%E2%80%94%E5%8F%8D%E5%90%91%E4%BC%A0%E6%92%AD%E7%AE%97%E6%B3%95/#%E9%97%AE%E9%A2%98%E6%8F%90%E5%87%BA

代码：

import torch

x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]

#赋予tensor中的data
w = torch.Tensor([1.0])#w初值为1
#设定w需要计算梯度grad
w.requires_grad = True

#模型y=x*w 建立计算图
def forward(x):
    '''
    w为Tensor类型
    x强制转换为Tensor类型
    通过这样的方式建立计算图
    '''
    return x * w

def loss(x, y):
    y_pred = forward(x)
    return (y_pred - y) ** 2

print ("predict  (before training)", 4, forward(4).item())

for epoch in range(100):
    for x,y in zip(x_data,y_data):
        #创建新的计算图
        l = loss(x,y)
        #进行反馈计算，此时才开始求梯度，此后计算图进行释放
        l.backward()
        #grad.item()取grad中的值变成标量
        print('\tgrad:',x, y, w.grad.item())
        #单纯的数值计算要利用data，而不能用张量，否则会在内部创建新的计算图
        w.data = w.data - 0.01 * w.grad.data
        #把权重梯度里的数据清零
        w.grad.data.zero_()
    print("progress:",epoch, l.item())

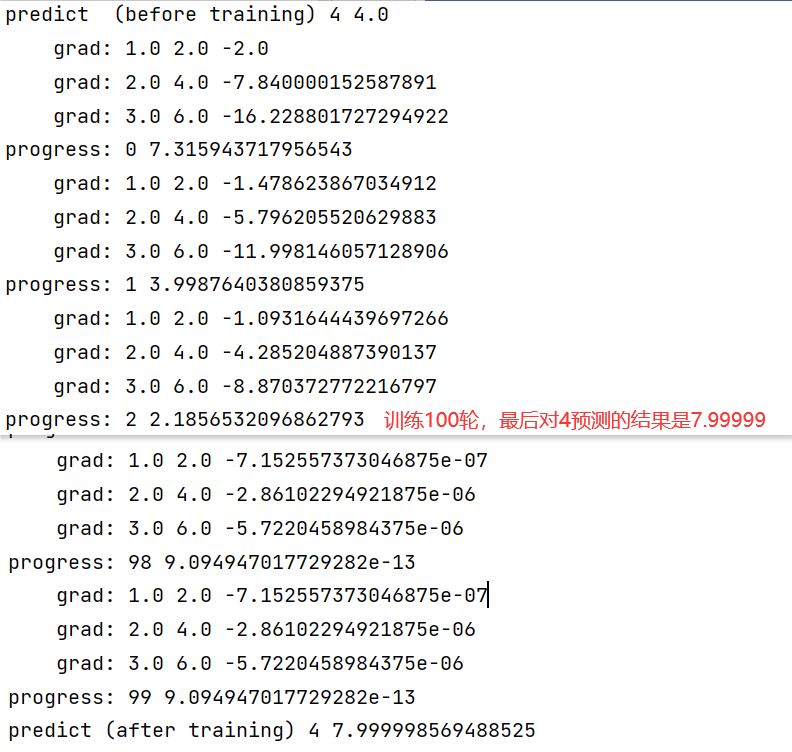
print("predict (after training)", 4, forward(4).item())