二叉树前中后序遍历的实现

1.非递归实现

1

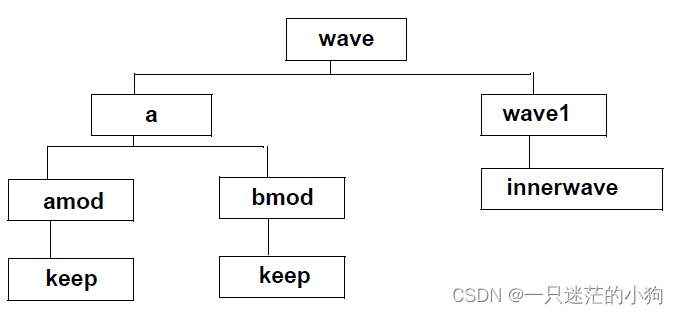
我们先回顾一下三种遍历：

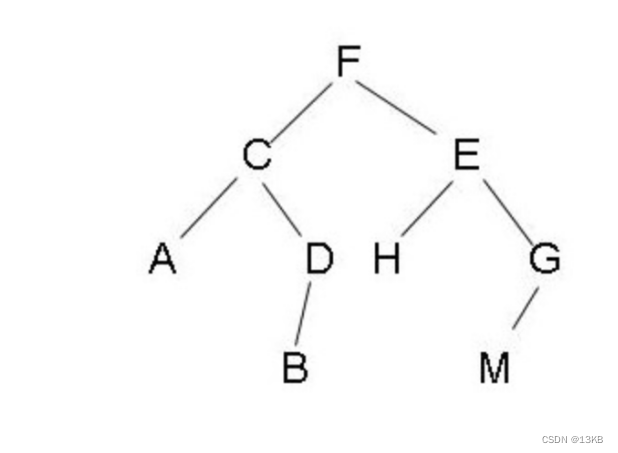
前序遍历：根->左->右： F-C-A -D-B-E-H-G-M
中序遍历：左->根->右： A-C-B-D-F-H-E-M-G
后序遍历：左->右->根： A-B-D-C-H-M-G-E-F

既然不用递归实现那其实我们可以用栈来实现。

对于前序：

1.判空：

如果根是空的话，return {}，注意他的函数返回类型是vector，所以加上｛｝。

2.建栈并压根

因为前序是根先出，所以先压入根。

3.出栈，依次压入左右子树

只要栈不为空就继续循环。
返回栈顶元素并删除栈顶元素。
如果有右子树先入右子树，因为栈是先进后出。所以右子树比左子树后出。
class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
     if(root==nullptr)
     {
         return{} ;
     }
     //用栈来实现二叉树
         vector<int> v;
         stack<TreeNode*> s;
         s.push(root);    //先压入root
         while(!s.empty())    //只要栈不为空就继续
         {
             TreeNode* top=s.top();
             v.push_back(top->val);
             s.pop();
           //先入根的右子树，才能让左子树先遍历
             if(top->right)
             {
                 s.push(top->right);
             }
             if(top->left)
             {
                 s.push(top->left);
             }
         }
     
     return v;
    }
};
中序遍历和前序遍历有点不一样。

1.判空
2.建栈，进入循环

栈不为空或者根节点不为空进入循环。
判断根节点是否为空，如果不为空，压入根，往左子树走。直到走到左子树的尽头，并且根为空。
如果根为空，说明最大的左子树已经遍历完了，所以返回栈顶元素，并且压入右子树但是是top->right而不是root->right,这个找的是离栈顶最近的右子树。
class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
    if(root==nullptr)
       {
         return{} ;
       }
     //用栈来实现二叉树
         vector<int> v;
         stack<TreeNode*> s;
         
         while(!s.empty()||root)    //只要栈不为空就继续
         {
             if(root)
             {
                 s.push(root);
                 root=root->left;
             }
             else
             {
                 TreeNode* top=s.top();
                 v.push_back(top->val);
                 s.pop();
                root=top->right;   //这里不再是root->right而是top->right
             }
         }
     
     return v;
    }
};
后序遍历：

后序遍历根前序遍历如出一辙，前面都一样，就是压入子树的顺序有点区别，这里是先压入左子树，此时栈里数据的顺序是根，右，左，然后我们用一个逆序函数，就变成左，右，根的顺序了。
class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
    if(root==nullptr)
     {
         return{} ;
     }
     //用栈来实现二叉树
         vector<int> v;
         stack<TreeNode*> s;
         s.push(root);    //先压入root
         while(!s.empty())    //只要栈不为空就继续
         {
             TreeNode* top=s.top();
             v.push_back(top->val);
             s.pop();
           //先入根的左子树，因为后面还有一个逆序呢
            
             if(top->left)
             {
                 s.push(top->left);
             }
             if(top->right)
             {
                 s.push(top->right);
             }
         }
     reverse(v.begin(),v.end());
     return v;
    }
};
现在还有兄弟问我while(!s.empty())啥意思，意思就是如果条件不为空，就继续。而不带！就是条件为真就继续，别搞混了。

2.递归实现

递归的思路相对更简单，我们写一个前序功能的函数完成根，左，右的遍历即可。

这里要用传引用，因为当不断插入数据时vector这个容器的数据会被修改。

class Solution {
public:
    void preorder(TreeNode* root,vector<int>& v)
    {
        if(root==nullptr)
        {
            return ;
        }
         v.push_back(root->val);
         preorder(root->left,v);
         preorder(root->right,v);
    }
    vector<int> preorderTraversal(TreeNode* root) {
      vector<int> v;
      preorder(root,v);
      return v;
    }
};

中后序就一笔带过了：

//中序遍历
class Solution {
public:
void inorder(TreeNode* root,vector<int>& v)
    {
        if(root==nullptr)
        {
            return ;
        }
       inorder(root->left,v);
       v.push_back(root->val);
       inorder(root->right,v);
       
    }
    vector<int> inorderTraversal(TreeNode* root)
   {
      vector<int> v;
     inorder(root,v);
     return v;
    }
};

//后序遍历
class Solution {
public:
  void postorder(TreeNode* root,vector<int>& v)
    {
        if(root==nullptr)
        {
            return ;
        }
         postorder(root->left,v);
         postorder(root->right,v);
          v.push_back(root->val);
    }
    vector<int> postorderTraversal(TreeNode* root) {
  
         vector<int> v;
         postorder(root,v);
         return v;
    }
};

3.Morris实现前中后序遍历

当我们用栈实现前序遍历时就会遇到一个无奈的问题，要想返回右子树的值，只能先让左子树的数据出栈后才能根据联系找到对应的右子树，但是Morris方法可以直接返回右子树。

它的核心思想就是：

Morris其实解决了一个常规循环中循环到叶子节点后难以回到根节点的问题。我们都知道前序遍历是先左后右，那么对任一节点p1来说，其右子树p1right所有节点必然在左子树p1left之后。代码中第二个while做的是，在p1left里一直往右，直到找不到更右的点，记这一点为p2。然后把p1接到p2的右边。这样既保证了p1right在p1left所有点之后，又不需要再回到p1节点。即在正常的往下循环的过程中，不断把右半部分剪下来，接到左半部分的最右下。

遍历原则：(curr初始化为根节点)
如果curr没有左孩子，curr就向右移动（curr = curr->right）
如果cur有左孩子，找到cur左子树上最右的节点，记为mostright

如果mostRight的right指针指向空，让其指向curr，cur向左移动（cur=cur->left）
如果mostright的right指针指向cur，让其指向空，cur向右移动（cur=cur->right）

前序遍历：
class Solution {
public: 
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> ans;
        if (root == NULL)
            return ans;
        TreeNode* curr = root;  // 当前的结点
        TreeNode* currLeft = NULL;  // 当前结点的左子树
        while (curr != NULL) 
        {
            currLeft = curr->left;
            // 当前结点的左子树存在即可建立连接
            if (currLeft != NULL) 
            {
                // 找到当前左子树的最右侧节点，并且不能沿着连接返回上层
                while (currLeft->right != NULL && currLeft->right != curr)
                    currLeft = currLeft->right;
                //最右侧节点的右指针没有指向根结点，创建连接并往下一个左子树的根结点进行连接操作
                if (currLeft->right == NULL) 
                {
                    currLeft->right = curr;
                    ans.push_back(curr->val);
                    curr = curr->left;
                    continue;  // 这个continue很关键
                } 
                else 
                // 当左子树的最右侧节点有指向根结点，此时说明我们已经进入到了返回上层的阶段，不再是一开始的建立连接阶段，同时在回到根结点时我们应已输出过下层节点，直接断开连接即可
                    currLeft->right = NULL;
            }
            else
                // 当前节点的左子树为空，说明左侧到头，直接输出
                ans.push_back(curr->val);
            // 返回上层的阶段不断向右走
            curr = curr->right;
        }
        return ans;
    }
};
中序遍历：

思路：
类似迭代，整个二叉树中输出的第一个节点是最左侧结点，因此在建立连接的时候是不能够直接输出的，必须在建立连接阶段完成，到达最左侧结点之后返回上层的阶段，才能开始输出，此时正好符合“左中右”的遍历方式。
特殊处理：

在建立连接阶段并不输出结点。
在找到最左侧结点（即根结点的左子树为空）时，开始向右走返回上层并同时输出当前结点。
对右子树也进行同样的处理。
class Solution {
public: 
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> ans;
        if (root == NULL)
            return ans;
        TreeNode* curr = root;  // 当前的结点
        TreeNode* currLeft = NULL;  // 当前结点的左子树
        while (curr != NULL) 
         {
            currLeft = curr->left;
            // 当前结点的左子树存在即可建立连接
            if (currLeft != NULL) 
            {
                // 找到当前左子树的最右侧节点，并且不能沿着连接返回上层
                while (currLeft->right != NULL && currLeft->right != curr)
                    currLeft = currLeft->right;
                //最右侧节点的右指针没有指向根结点，创建连接并往下一个左子树的根结点进行连接操作
                if (currLeft->right == NULL) 
                {
                    currLeft->right = curr;
                    curr = curr->left;
                    continue;  // 这个continue很关键
                } 
                else 
                // 当左子树的最右侧节点有指向根结点，此时说明我们已经进入到了返回上层的阶段，不再是一开始的建立连接阶段，同时在回到根结点时我们应已输出过下层节点，直接断开连接即可
                    currLeft->right = NULL;
            }
            // 当前节点的左子树为空，说明左侧到头，直接输出并返回上层
            ans.push_back(curr->val);
            // 返回上层的阶段不断向右走
            curr = curr->right;
        }
        return ans;
    }
};
这是我复制力扣上一位大佬的代码，写的很不错。后序各位有兴趣去看看大佬写的，我不在列出来了。

作者：bei-zhi-hu
链接：https://leetcode.cn/problems/binary-tree-preorder-traversal/solution/cer-cha-shu-san-