前言

实现滑动窗口，主要确定如下三点：

窗口内是什么？
如何移动窗口的起始位置？
如何移动窗口的结束位置？

一、长度最小的子数组

给定一个含有 n 个正整数的数组和一个正整数 s ，找出该数组中满足其和 ≥ s 的长度最小的连续子数组，并返回其长度。如果不存在符合条件的子数组，返回 0。
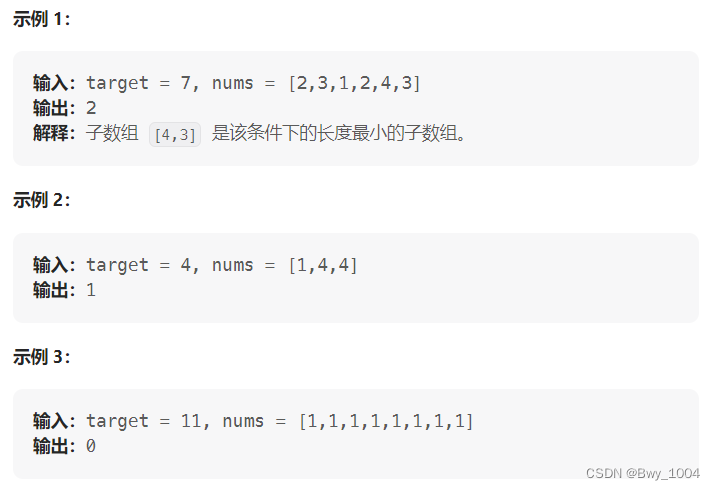
在这里插入图片描述

1、暴力求解：

两个for循环，然后不断的寻找符合条件的子序列，时间复杂度很明显是O(n^2)。

class Solution {
    public int minSubArrayLen(int target, int[] nums) {
        int result=Integer.MAX_VALUE;
        int sum=0;
        int subLength=0;
        for(int i=0;i<nums.length;i++){ //起点
            sum=0;
            for(int j=i;j<nums.length;j++){ //终点
                sum+=nums[j];
                if(sum>=target){//更新result
                    subLength=j-i+1;
                    result=Math.min(result,subLength);
                    break;
                }
            }
        }
    return result == Integer.MAX_VALUE? 0 : result;
    }
}

在这里插入图片描述

2、滑动窗口求解：

所谓滑动窗口，就是不断的调节子序列的起始位置和终止位置，从而得出我们要想的结果。

在暴力解法中，是一个for循环滑动窗口的起始位置，一个for循环为滑动窗口的终止位置，用两个for循环完成了一个不断搜索区间的过程。
滑动窗口用一个for循环来完成这个操作，那么这个循环的索引，一定是表示滑动窗口的终止位置。

class Solution {
    public int minSubArrayLen(int target, int[] nums) {
        int result=Integer.MAX_VALUE;
        int sum=0;
        int subLength=0;
        int i=0;
        for(int j=0;j<nums.length;j++){ //终点
            sum+=nums[j];
            while(sum>=target){
                subLength=j-i+1;
                result=Math.min(result,subLength);
                sum -= nums[i++];
            }
        }
    return result == Integer.MAX_VALUE? 0 : result;
    }
}

在这里插入图片描述

二、最小覆盖子串（乐扣76）难难难难难

给一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串，则返回空字符串 “” 。
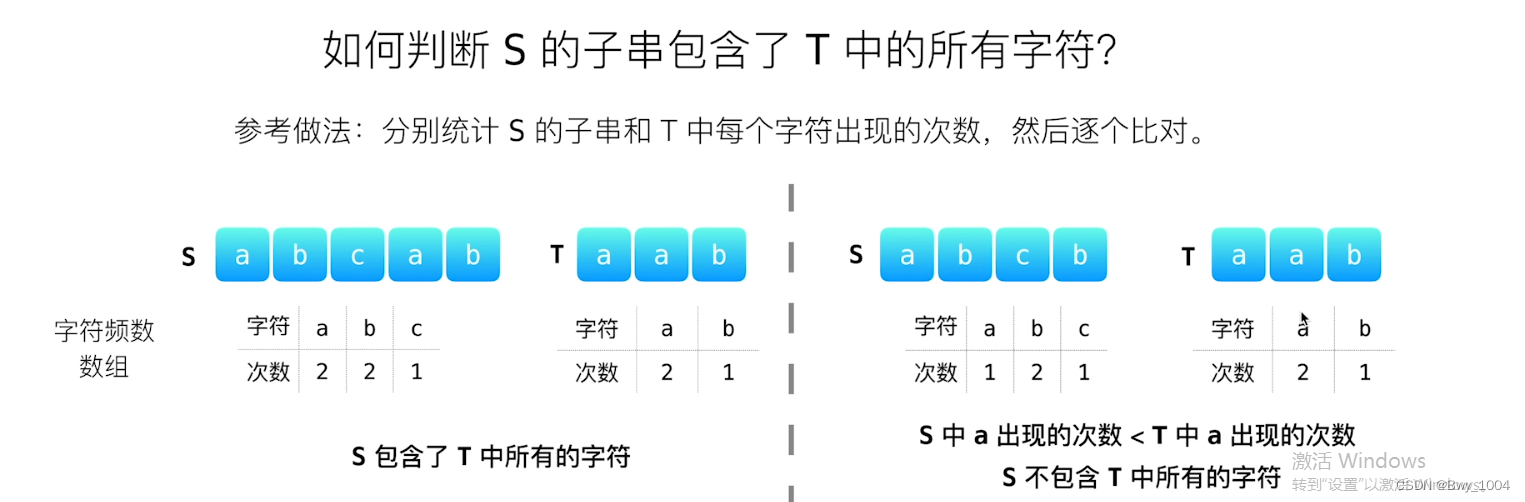
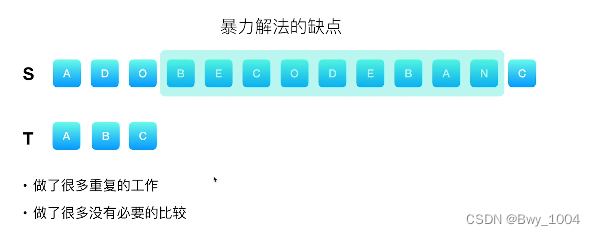
在这里插入图片描述
暴力求解：

在这里插入图片描述

滑动窗口求解：

class Solution {
    public String minWindow(String s, String t) {
        int sLen=s.length();
        int tLen=t.length();
        if(sLen==0||tLen==0||sLen<tLen){
            return "";
        }
        //将字符串转为字符数组
        char[] charArrayS = s.toCharArray();
        char[] charArrayT = t.toCharArray();

        //两个字符频数数组
        int[] winFreq = new int[128];
        int[] tFreq = new int[128];
        for(char c :charArrayT){
            tFreq[c]++;
        }

        //滑动窗口内部包含多少T中的字符，对应字符频数超过不重复计算
        int distance =0;
        int minLen = sLen+1;
        int begin=0;

        int left=0; //滑动窗口左边界
        int right=0;  //滑动窗口右边界
        //[left,right) 左闭右开
        while(right<sLen){  //[0,0)
            //在t当中不出现
            if(tFreq[charArrayS[right]]==0){
                right++;
                continue;
            }
            if(winFreq[charArrayS[right]] < tFreq[charArrayS[right]]){
                distance++;
            }
            winFreq[charArrayS[right]]++;
            right++;
            //左边界
            while(distance==tLen){
                //左边界向右移动
                if(right-left<minLen){
                    minLen=right-left;
                    begin=left;
                }
                 if(tFreq[charArrayS[left]]==0){
                    left++;
                    continue;
                }
                if(winFreq[charArrayS[left]] == tFreq[charArrayS[left]]){
                    distance--;
                }
                winFreq[charArrayS[left]]--;
                left++;
            }
        }
        if(minLen==sLen+1){ //没有更新的话
            return "";
        }
        return s.substring(begin,begin+minLen);
    }
}

在这里插入图片描述

三、水果成篮（乐扣904）

你正在探访一家农场，农场从左到右种植了一排果树。这些树用一个整数数组 fruits 表示，其中 fruits[i] 是第 i 棵树上的水果种类。
你想要尽可能多地收集水果。然而，农场的主人设定了一些严格的规矩，你必须按照要求采摘水果：
只有两个篮子，并且每个篮子只能装单一类型的水果。每个篮子能够装的水果总量没有限制。
可以选择任意一棵树开始采摘，你必须从每棵树（包括开始采摘的树）上恰好摘一个水果。采摘的水果应当符合篮子中的水果类型。每采摘一次，你将会向右移动到下一棵树，并继续采摘。
一旦你走到某棵树前，但水果不符合篮子的水果类型，那么就必须停止采摘。
给你一个整数数组 fruits ，返回你可以收集的水果的最大数目。
在这里插入图片描述
运用滑动窗口求解：

class Solution {
    public int totalFruit(int[] fruits) {
        int size = fruits.length;
        int[] kindMap = new int[size];
        int i=0;
        int kind=0;
        int maxVariety=1;
        for(int j=0;j<fruits.length;j++){
            if(kindMap[fruits[j]]==0){
                kind++;
            }
            kindMap[fruits[j]]++; //将该水果放入篮子
            while(kind>2){
                kindMap[fruits[i]]--;
                if(kindMap[fruits[i]]==0)kind--;
                i++;
            }
        maxVariety = Math.max(maxVariety,j-i+1);
        }
        return maxVariety;
    }
}