👨‍🎓个人主页：研学社的博客 

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

---

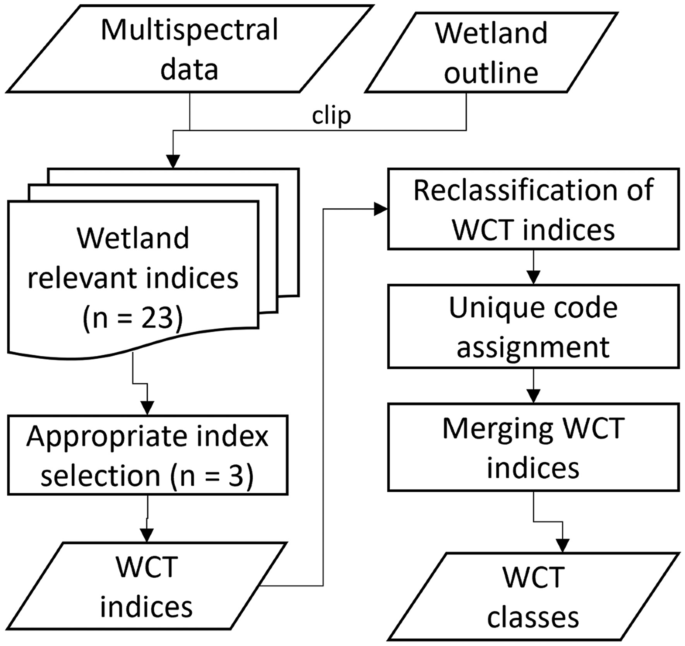
💥1 概述

针对迭代后期搜索多样性不足、易陷入局部最优的问题，提出一种基于Levy飞行扰动策略的改进麻雀搜索算法。首先，利用Sin混沌搜索机制改进种群初始化策略。然后将Levy飞行扰动机制引入到麻雀种群的觅食搜索过程中，以拖拽种群移动合适的步长，增加空间搜索的多样性。

📚2 运行结果

 

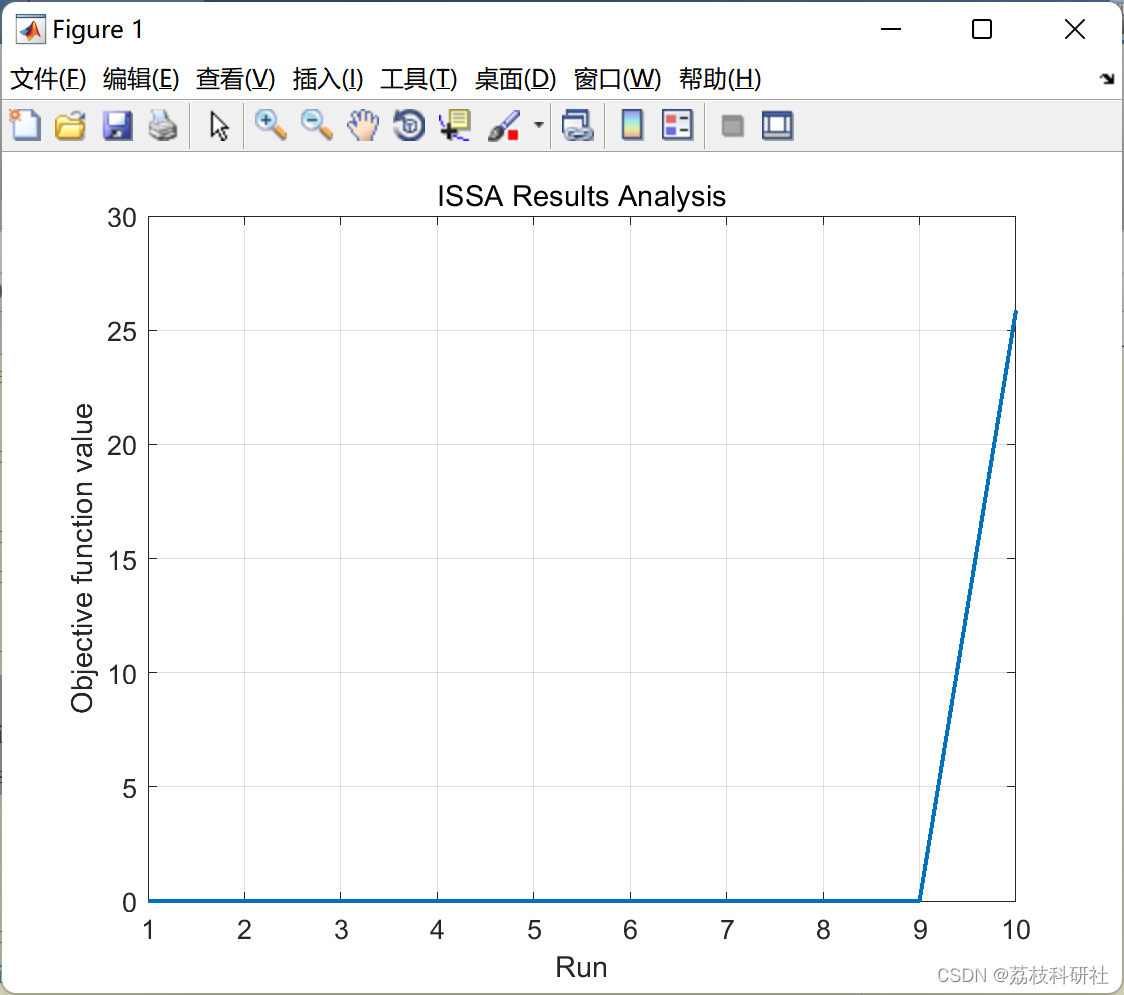
部分代码：

function [FoodFit,FoodPos,ConvCurve]=ISSA(Ntot,Ninit,tMax,LoB,UpB,Nvars,fobj)
%% Set parameters
% Percentage (nSOF) / number (NSOF) of inidividuals that are replaced by 
% the Survival of the Fittest Mechanism 
nSOF = 0.05; NSOF = round((1-nSOF) * Ntot);

% Min. and Max. Mutation Probability value
pMUTmax = 0.15 ; pMUTmin = 0.1;

% Min. and Max. Crossover Probability value
pCRSmax = 0.25 ; pCRSmin = 0.1;

% Min. and Max. Numberof Exploring Salps
NexpMax = round(Ntot * 0.5); NexpMin = 1;

%% Initialization
ConvCurve = zeros(1,tMax);
FoodPos = zeros(1,Nvars);
SalpFit = zeros(Ninit,1);

%% Initialize the positions of salps

nPos = ceil(Ninit/2);
Pos = rand(nPos,Nvars).*(UpB-LoB)+LoB;
OpPos = UpB + LoB - Pos;
SalpPos = [Pos;OpPos];
if mod(Ninit,2)
    SalpPos(end,:)=[];
end

for i=1:Ninit
    SalpFit(i,1)=fobj(SalpPos(i,:));
end

[SalpFit,sortIndex]=sort(SalpFit);
SalpPos = SalpPos(sortIndex,:);
SalpPos(Ntot+1:end,:) = [];
SalpFit(Ntot+1:end,:) = [];
FoodPos = SalpPos(1,:);
FoodFit = SalpFit(1);
ConvCurve(1) = FoodFit;

%% Main loop
t = 2; % First iteration was the initialization
while t <= tMax
    % Compute c1 parameter
    c1 = 2 * exp(-(4 * t / tMax) ^ 2);
    % Compute   Nexp (exploring salps number),
    %           pMUT (mutation probability),
    %           and pCRS (crossover probability).
    Nexp = round(NexpMax * (t / tMax) + NexpMin);  % Pun un round aici
    pMUT = pMUTmax * (1- t / tMax) + pMUTmin;
    pCRS = pCRSmax * t / tMax + pCRSmin;
    
    for i = 1 : Ntot
        % Update the leader and the exploring salps
        if i <= Nexp
            for j = 1 : Nvars
                c2 = rand(); % Random weights
                c3 = rand(); % Random number to decide the sign
                c4 = rand; % Random number to decide if crossover applies
                
                % Update the exploring salps using the first variant of crossover
                if c4 < pCRS / 2
                    SalpPos(i,j) = FoodPos(j) * c2 + SalpPos(i,j) * (1 - c2);
                    
                    % Update the exploring salps using the second variant of crossover
                elseif c4 < pCRS
                    SalpPos(i,j) = FoodPos(j) * (1-c2 / 2) + SalpPos(i,j) * (c2 / 2);
                    
                    % Update the exploring salps using the equation from the leader salp
                else
                    if c3 < 0.5 % Decide the sign + or -
                        SalpPos(i,j) = FoodPos(j) + c1 * ((UpB(j) - LoB(j)) * c2 + LoB(j));
                    else
                        SalpPos(i,j) = FoodPos(j) - c1 * ((UpB(j) -LoB(j)) * c2 + LoB(j));
                    end
                end
            end % for j = 1 : Nvars
            
            % Update the follower salps
        elseif    i > Nexp && i < NSOF
            % The first follower salp is guided by the Food Position
            if i == Nexp + 1
                Salp1 = FoodPos;
                % All the others are guided by the previous salp
            else
                Salp1 = SalpPos(i-1,:);
            end
            Salp2 = SalpPos(i,:);
            
            if rand() > pMUT
                % The new position is determined as weighted average between
                % the previous and current salp
                r1 = rand(); % Random weight
                SalpPos(i,:) = Salp2 * r1 + Salp1 * (1 - r1); % fara 1/2 asta!!!!!
                
                % Mutation is applied with the pMUT probability
            else
                r1 = rand(1,Nvars); % Random weight
                r2 = sign(rand(1,Nvars) - 0.5); % Random number to decide the sign
                SalpPos(i,:) = SalpPos(randi(Ntot),:) + r1 .* (r2 .*(UpB-LoB)+LoB) * c1;
            end
            
            % Eliminate the weakest salps and replace them with new random
            % salps
        elseif i>=NSOF && i<=Ntot
            SalpPos(i,:) = rand(1,Nvars) .* (UpB - LoB) + LoB;
        end
        
        % Enforce Boundaries by replacing the value that violates a limit
        % with the violated limit
        Fupb=find(SalpPos(i,:)>UpB);
        Flob=find(SalpPos(i,:)<LoB);
        SalpPos(i,Fupb) = UpB(1,Fupb);
        SalpPos(i,Flob) = LoB(1,Flob);
        
        % Compute the salp fitnes
        SalpFit(i,1) = fobj(SalpPos(i,:));
        
        % If necessary update the Food Position and Fitness
        if SalpFit(i,1) < FoodFit
            FoodPos = SalpPos(i,:);
            FoodFit = SalpFit(i,1);
        end
    end % for i = 1 : Ntot
    
    % Sort the salps
    [SalpFit,sortIndex] = sort(SalpFit);
    SalpPos = SalpPos(sortIndex,:);
    
    % Update the converge curve
    ConvCurve(t)=FoodFit;
    
    if 0% mod(l,10) == 0
        display([t,FoodFit]);
    end
    % Increment iteration
    t = t + 1;
end % while t <= tMax
end % function

🎉3 参考文献

部分理论来源于网络，如有侵权请联系删除。

  Andrei M. Tudose, Irina I. Picioroaga, Dorian O. Sidea, Constantin Bulac  Solving single- and multi-objective optimal reactive power dispatch 
  problem using an improved salp swarm algorithm
 

🌈4 Matlab代码实现