目录
1 概述
2 数学模型
2.1 目标函数
2.2 约束条件
2.3 Jaya 算法
3 仿真结果
4 Matlab代码实现
1 概述
最优潮流计算与电力系统的稳定、经济运行密切相关,自20世纪60年代提出最优潮流的概念,大量学者相继提出了各种优化技术来求解电力系统的最优潮流问题。Jaya算法是于2016年提出的一种简单高效的新型优化算法,具有收敛快寻优强的特点。算例在IEEE39节点上实现。
2 数学模型
2.1 目标函数

目标函数(Matlab代码实现)
function [F,Plosses] = ObjectiveFunction(V_o,line_o,Bgen,Theta_o,nbranch,FromNode,ToNode,PQ)
%% 该函数计算目标函数,包含惩罚项因子
for k=1:nbranch
a(k)=line_o(k,6);
if a(k)==0 % 在这种情况下,我们正在分析线路
Zpq(k)=line_o(k,3)+1i*line_o(k,4); % 线路阻抗
Ypq(k)=Zpq(k)^-1; % 线路导纳
gpq(k)=real(Ypq(k)); % 线路电导
%+++++++++++目标函数1,系统网损+++++++++++
Llpq(k)=gpq(k)*(V_o(FromNode(k))^2 +V_o(ToNode(k))^2 -2*V_o(FromNode(k))*V_o(ToNode(k))*cos(Theta_o(FromNode(k))-Theta_o(ToNode(k))));
end
end
%% 有功总损耗
Plosses=sum(Llpq);
%% 目标函数
KL=1000; % 惩罚因子
for k=1:length(PQ)
%% 负载电压偏移(0.95~1.05)
if V_o(k+length(Bgen))<0.95 %电压偏移小于0.95
DVL(k)=0.95-V_o(k+length(Bgen)); %惩罚项1
end
if V_o(k+length(Bgen))>1.05 %电压偏移大于1.05
DVL(k)=V_o(k+length(Bgen))-1.05; %惩罚项2
end
if V_o(k+length(Bgen))>=0.95 %电压偏移如果在0.95~1.05之间
if V_o(k+length(Bgen))<=1.05
DVL(k)=0; %电压偏移惩罚项为零
end
end
end
DVLoads=sum(DVL.*DVL);
Z=Plosses+KL*DVLoads; %目标函数
F=Z; % 目标函数
end
function [F,Plosses] = ObjectiveFunction(V_o,line_o,Bgen,Theta_o,nbranch,FromNode,ToNode,PQ)
%% 该函数计算目标函数,包含惩罚项因子
for k=1:nbranch
a(k)=line_o(k,6);
if a(k)==0 % 在这种情况下,我们正在分析线路
Zpq(k)=line_o(k,3)+1i*line_o(k,4); % 线路阻抗
Ypq(k)=Zpq(k)^-1; % 线路导纳
gpq(k)=real(Ypq(k)); % 线路电导
%+++++++++++目标函数1,系统网损+++++++++++
Llpq(k)=gpq(k)*(V_o(FromNode(k))^2 +V_o(ToNode(k))^2 -2*V_o(FromNode(k))*V_o(ToNode(k))*cos(Theta_o(FromNode(k))-Theta_o(ToNode(k))));
end
end
%% 有功总损耗
Plosses=sum(Llpq);
%% 目标函数
KL=1000; % 惩罚因子
for k=1:length(PQ)
%% 负载电压偏移(0.95~1.05)
if V_o(k+length(Bgen))<0.95 %电压偏移小于0.95
DVL(k)=0.95-V_o(k+length(Bgen)); %惩罚项1
end
if V_o(k+length(Bgen))>1.05 %电压偏移大于1.05
DVL(k)=V_o(k+length(Bgen))-1.05; %惩罚项2
end
if V_o(k+length(Bgen))>=0.95 %电压偏移如果在0.95~1.05之间
if V_o(k+length(Bgen))<=1.05
DVL(k)=0; %电压偏移惩罚项为零
end
end
end
DVLoads=sum(DVL.*DVL);
Z=Plosses+KL*DVLoads; %目标函数
F=Z; % 目标函数
end
2.2 约束条件

2.3 Jaya 算法
Jaya 算法是 Rao 等提出的一种元启发式算法,它基于持续改进的原理,将个体不断向优秀个体靠拢,同时不断远离差的个体,进而不断提高解的质量。传统 Jaya 算法主要基于迭代公式,每次通过该方程迭代进化获取新的解,因此 Jaya 算法不像其他进化算法需要许多的参数,它只需要针对特定问题调整迭代过程的参数,减少了因为调整过多参数而带来的测试上的麻烦。与其它元启发式算法相比,Jaya 算法更容易理解和实现。该算法的迭代公式如下所示:
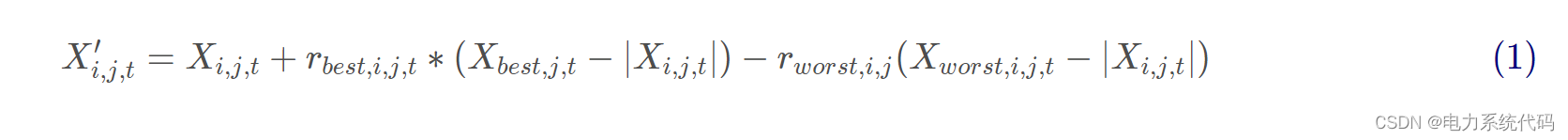

Jaya优化算法流程图如下:

目标函数:
%% 基于Jaya算法的电力系统最优潮流
%% 有功损耗最小化
clear all;
close all;
clc
%% ++++++++++++++++电力系统数据库+++++++++++++++
% 下面的文件包含了母线、线路矩阵等电力系统拓扑信息
data_39;
% 线路类型和发电机
bus_o=bus; line_o=line;
slack=find(bus(:,10)==1); % 松弛节点/平衡节点
PV=find(bus(:,10)==2); % PV节点
Bgen=vertcat(slack,PV); %平衡节点和松弛节点【C = vertcat(A,B) 将 B 垂直串联到 A 的末尾。】
PQ=find(bus(:,10)==3); % PQ节点/负荷节点
%% +++++++++++++++ 优化算法的参数 ++++++++++++++++
pop = 210; % 种群规模
n_itera = 35; % 优化算法迭代次数
Vmin=0.95; % 发电机电压的最小值
Vmax=1.05; % 发电机电压的最大值
mini_tap = 0.95; % TAP的最小值
maxi_tap = 1.05; % TAP的最大值
Smin=-0.5; % 视在功率最小值
Smax=0.5; % 视在功率最大值
pos_Shunt = find( bus(:,11) ~= 0); % 母线矩阵中分流点的位置
pos_tap = find( line(:,6) ~= 0); % TAPs在行矩阵中的位置
tap_o = line(pos_tap,6); % TAPs初始值
Shunt_o = bus(pos_Shunt,9); %分流器的初始值
n_tap = length(pos_tap); % TAPs的数量
n_Shunt = length(pos_Shunt); % 分流器的数量
n_nodos = length(bus(:,1)); % 电力系统的节点数量
%% ++++++++++++++++ 第一:运行基本情况下的潮流 ++++++++++++++++
% 存储基本情况的电压和相角
[V_o,Theta_o,~] = PowerFlowClassical(bus_o,line_o);
%% +++++++++++++++++++计算有功功率损耗++++++++++++++++++++++
nbranch=length(line_o(:,1));
FromNode=line_o(:,1);
ToNode=line_o(:,2);
for k=1:nbranch
a(k)=line_o(k,6);
if a(k)==0 % 在这种情况下,我们正在分析线路
Zpq(k)=line_o(k,3)+1i*line_o(k,4); % 线路的阻抗
Ypq(k)=Zpq(k)^-1; % 线路导纳
gpq(k)=real(Ypq(k)); % 线路电导
% 对应线路有功损耗
Llpq(k)=gpq(k)*(V_o(FromNode(k))^2 +V_o(ToNode(k))^2 -2*V_o(FromNode(k))*V_o(ToNode(k))*cos(Theta_o(FromNode(k))-Theta_o(ToNode(k))));
end
end
% 有功总损耗
Plosses=sum(Llpq);
%% +++++++++++++++++++++++++++ 最优潮流 ++++++++++++++++++++++++++
% 启动种群
for k=1:n_tap % 启动TAP种群
x_tap(:,k) = mini_tap +(maxi_tap - mini_tap)*(0.1*floor((10*rand(pop,1))));
end
for k=1:n_Shunt % 启动分流种群
x_shunt(:,k) = Smin +(Smax - Smin)*(0.1*floor((10*rand(pop,1))));
end
for k=1:length(Bgen) % 从发电机启动电压的种群
x_vg(:,k) = Vmin +(Vmax - Vmin)*(0.1*floor((10*rand(pop,1))));
end
%% JAYA 算法
for k=1:n_itera
% 使用TAP的新值,分流和发电机电压重新计算电压和节点导纳
%修改线路和母线矩阵
for p=1:pop
for q=1:n_tap
r=pos_tap(q);
line(r,6)=x_tap(p,q); % 根据新的TAP值对线矩阵进行修正
end; clear r
for qa=1:n_Shunt
r=pos_Shunt(qa);
bus(r,9)=x_shunt(p,qa); % 根据新的分流值修改母线矩阵
end; clear r
for qb=1:length(Bgen)
r=Bgen(qb);
bus(r,2)=x_vg(p,qb); %根据新的VG值修改总线矩阵
end
% 随着新的线路和母线矩阵运行潮流
[V_n,Theta_n,~] = PowerFlowClassical(bus,line);
% 目标函数
[F,~] = ObjectiveFunction(V_n,line_o,Bgen,Theta_n,nbranch,FromNode,ToNode,PQ);
Ofun=F; Obfun(k,p)=F;
end
%% 基于Jaya算法的电力系统最优潮流
%% 有功损耗最小化
clear all;
close all;
clc
%% ++++++++++++++++电力系统数据库+++++++++++++++
% 下面的文件包含了母线、线路矩阵等电力系统拓扑信息
data_39;
% 线路类型和发电机
bus_o=bus; line_o=line;
slack=find(bus(:,10)==1); % 松弛节点/平衡节点
PV=find(bus(:,10)==2); % PV节点
Bgen=vertcat(slack,PV); %平衡节点和松弛节点【C = vertcat(A,B) 将 B 垂直串联到 A 的末尾。】
PQ=find(bus(:,10)==3); % PQ节点/负荷节点
%% +++++++++++++++ 优化算法的参数 ++++++++++++++++
pop = 210; % 种群规模
n_itera = 35; % 优化算法迭代次数
Vmin=0.95; % 发电机电压的最小值
Vmax=1.05; % 发电机电压的最大值
mini_tap = 0.95; % TAP的最小值
maxi_tap = 1.05; % TAP的最大值
Smin=-0.5; % 视在功率最小值
Smax=0.5; % 视在功率最大值
pos_Shunt = find( bus(:,11) ~= 0); % 母线矩阵中分流点的位置
pos_tap = find( line(:,6) ~= 0); % TAPs在行矩阵中的位置
tap_o = line(pos_tap,6); % TAPs初始值
Shunt_o = bus(pos_Shunt,9); %分流器的初始值
n_tap = length(pos_tap); % TAPs的数量
n_Shunt = length(pos_Shunt); % 分流器的数量
n_nodos = length(bus(:,1)); % 电力系统的节点数量
%% ++++++++++++++++ 第一:运行基本情况下的潮流 ++++++++++++++++
% 存储基本情况的电压和相角
[V_o,Theta_o,~] = PowerFlowClassical(bus_o,line_o);
%% +++++++++++++++++++计算有功功率损耗++++++++++++++++++++++
nbranch=length(line_o(:,1));
FromNode=line_o(:,1);
ToNode=line_o(:,2);
for k=1:nbranch
a(k)=line_o(k,6);
if a(k)==0 % 在这种情况下,我们正在分析线路
Zpq(k)=line_o(k,3)+1i*line_o(k,4); % 线路的阻抗
Ypq(k)=Zpq(k)^-1; % 线路导纳
gpq(k)=real(Ypq(k)); % 线路电导
% 对应线路有功损耗
Llpq(k)=gpq(k)*(V_o(FromNode(k))^2 +V_o(ToNode(k))^2 -2*V_o(FromNode(k))*V_o(ToNode(k))*cos(Theta_o(FromNode(k))-Theta_o(ToNode(k))));
end
end
% 有功总损耗
Plosses=sum(Llpq);
%% +++++++++++++++++++++++++++ 最优潮流 ++++++++++++++++++++++++++
% 启动种群
for k=1:n_tap % 启动TAP种群
x_tap(:,k) = mini_tap +(maxi_tap - mini_tap)*(0.1*floor((10*rand(pop,1))));
end
for k=1:n_Shunt % 启动分流种群
x_shunt(:,k) = Smin +(Smax - Smin)*(0.1*floor((10*rand(pop,1))));
end
for k=1:length(Bgen) % 从发电机启动电压的种群
x_vg(:,k) = Vmin +(Vmax - Vmin)*(0.1*floor((10*rand(pop,1))));
end
%% JAYA 算法
for k=1:n_itera
% 使用TAP的新值,分流和发电机电压重新计算电压和节点导纳
%修改线路和母线矩阵
for p=1:pop
for q=1:n_tap
r=pos_tap(q);
line(r,6)=x_tap(p,q); % 根据新的TAP值对线矩阵进行修正
end; clear r
for qa=1:n_Shunt
r=pos_Shunt(qa);
bus(r,9)=x_shunt(p,qa); % 根据新的分流值修改母线矩阵
end; clear r
for qb=1:length(Bgen)
r=Bgen(qb);
bus(r,2)=x_vg(p,qb); %根据新的VG值修改总线矩阵
end
% 随着新的线路和母线矩阵运行潮流
[V_n,Theta_n,~] = PowerFlowClassical(bus,line);
% 目标函数
[F,~] = ObjectiveFunction(V_n,line_o,Bgen,Theta_n,nbranch,FromNode,ToNode,PQ);
Ofun=F; Obfun(k,p)=F;
end
完整代码:Jaya算法在电力系统最优潮流计算中的应用(创新点)
3 仿真结果
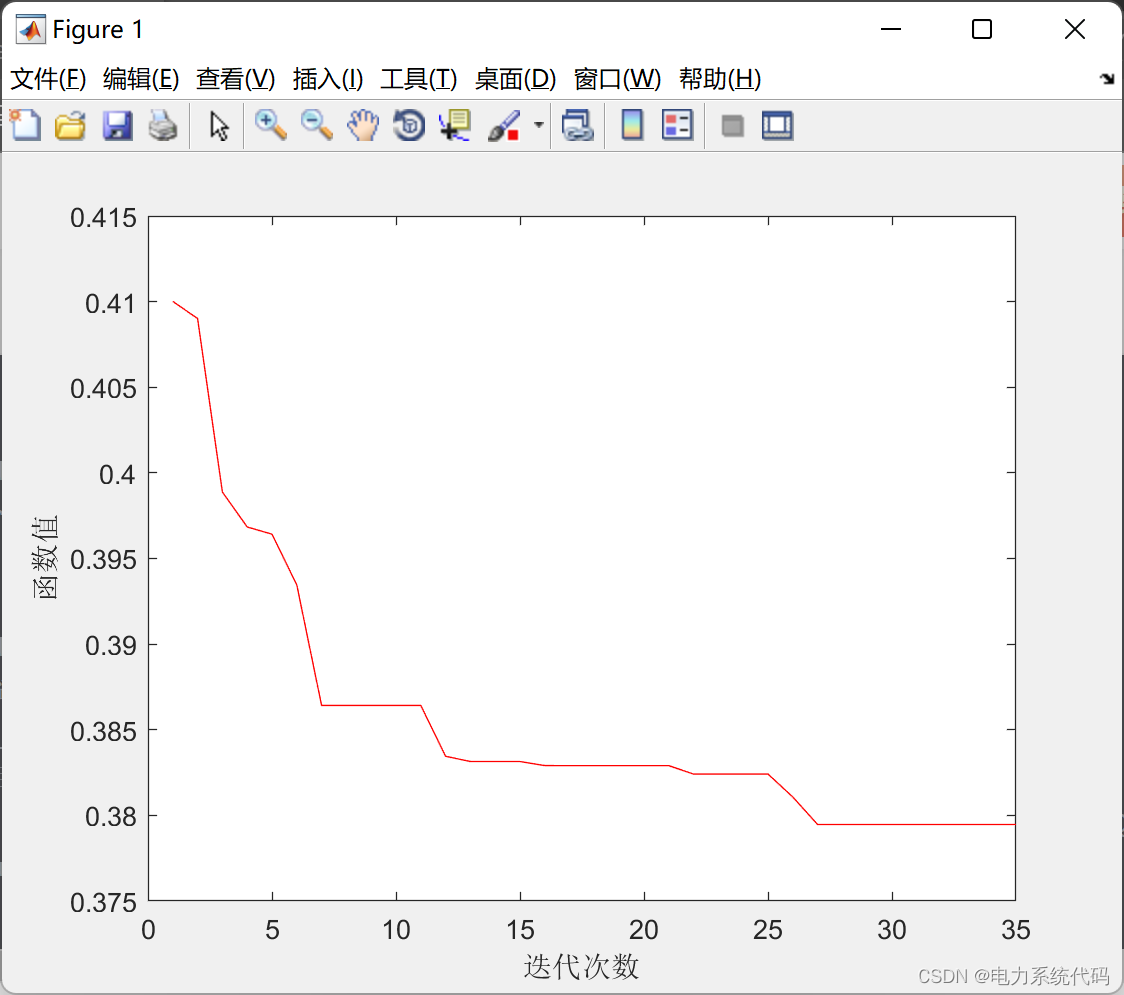

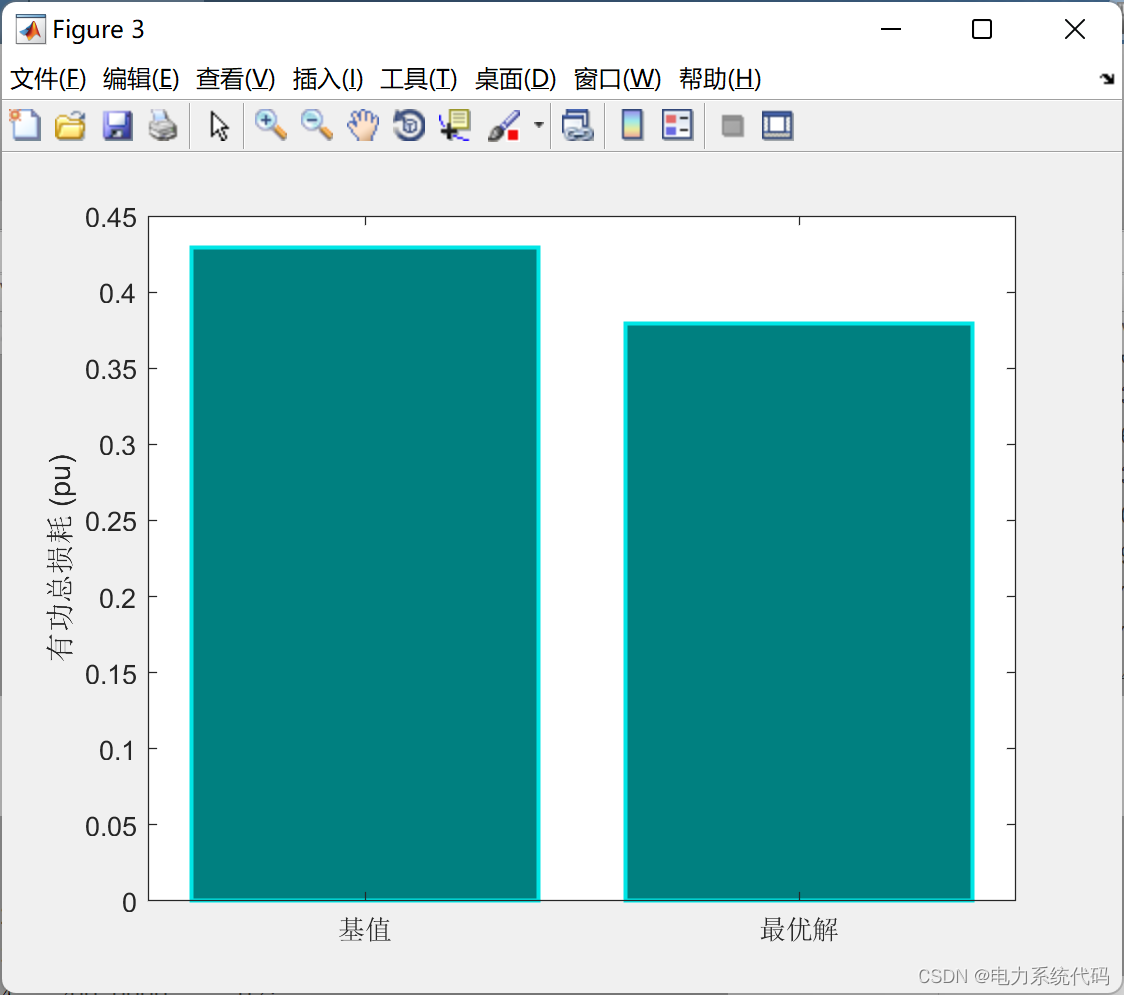
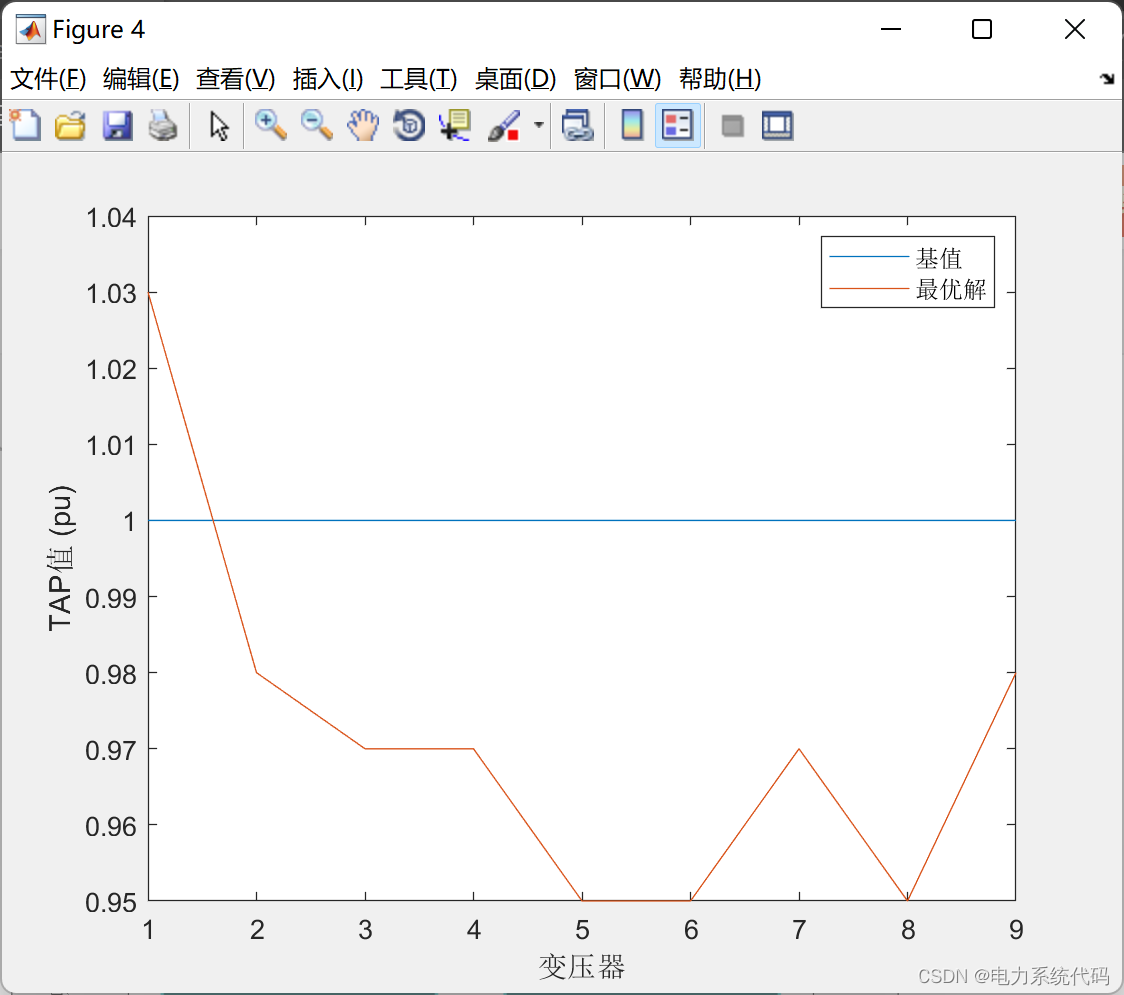
4 Matlab代码实现
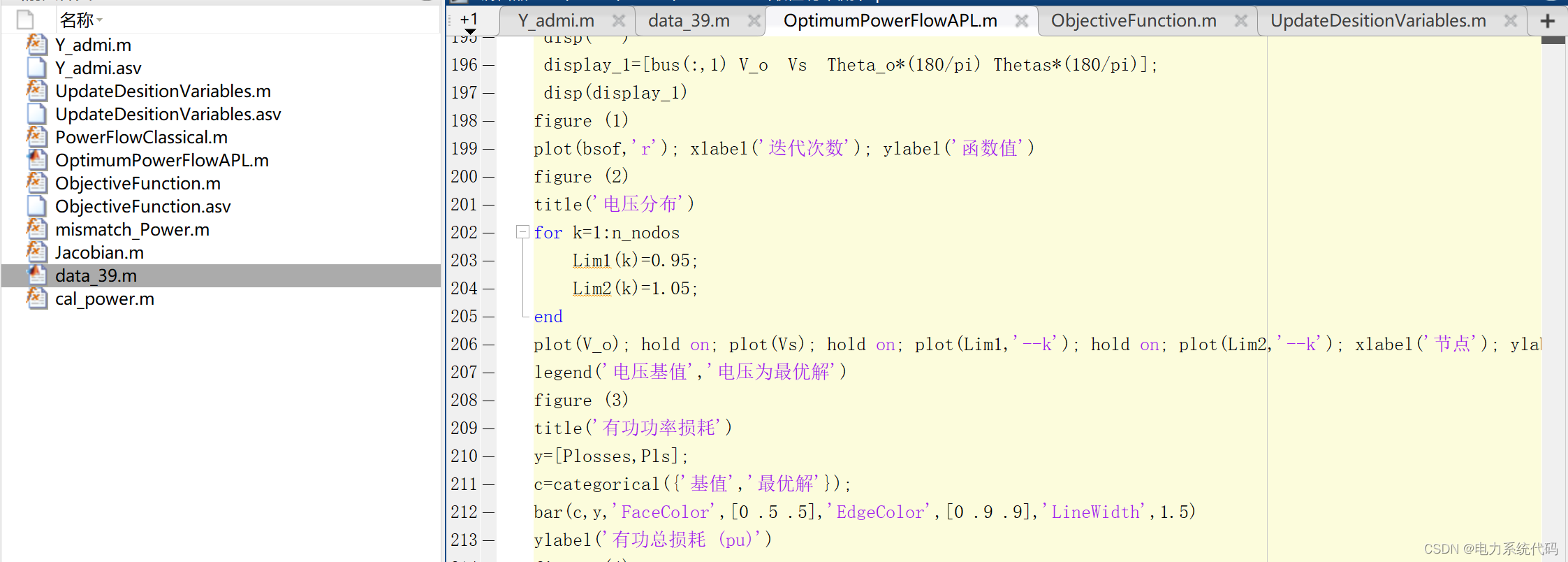




![[附源码]java毕业设计学生宿舍设备报修](https://img-blog.csdnimg.cn/4f8df232298447a4949ce589f0438632.png)