random recording 随心记录
What seems to us as bitter trials are often blessings in disguise.
看起来对我们痛苦的试炼，常常是伪装起来的好运。

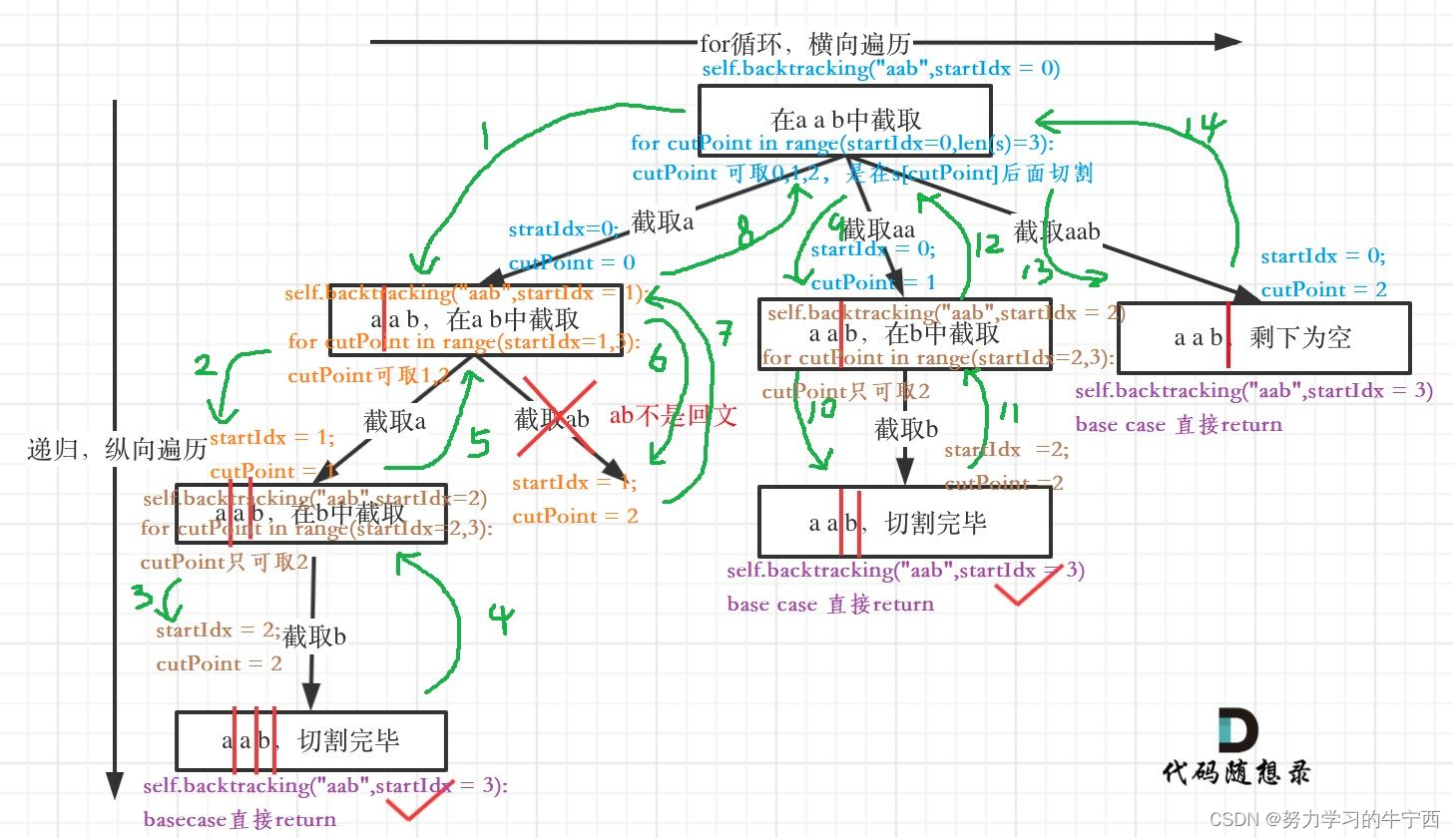
大O表示法是一种特殊的表示法，指出了算法的速度有多快。

背景引入

Bob要为NASA编写一个查找算法，这个算法在火箭即将登陆月球前开始执行，帮助计算着陆地点。Bob使用包含10亿个元素的列表运行二分查找，运行时间为30毫秒（log21000000000大约为30），简单查找需要10亿毫秒，相当于11天。

二分查找和简单查找的运行时间的增速不同，仅知道算法需要多长时间才能运行完毕还不够，还需知道运行时间如何随列表增长而增加，引出了大O表示。

理解不同的大O运行时间

问题:假设你要画一个网格，它包含16个格子。

算法1

以每次画一个的方式画16个格子,以每次画一个的方式画16个格子,运行时间为O(n)，对比简单查找。

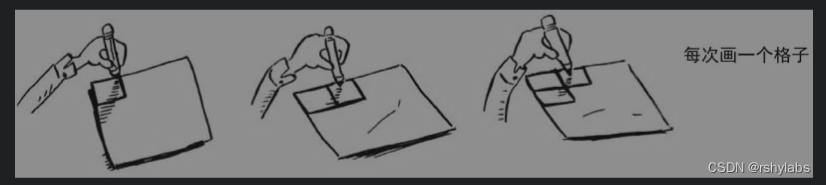
算法2

将纸折起来,运行时间为O(log n)，对比二分查找。

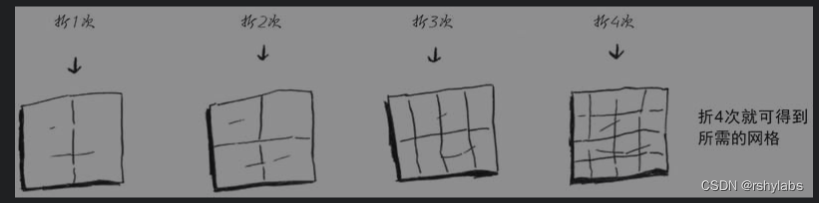
一些常见的大O运行时间

大O表示法指出了最糟情况下的运行时间

• O(log n)，也叫对数时间，这样的算法包括二分查找。
• O(n)，也叫线性时间，这样的算法包括简单查找。
• O(n ＊ log n)，快速排序——一种速度较快的排序算法。
• O(n2)，选择排序——一种速度较慢的排序算法。
• O(n! )，旅行商问题的解决方案——一种非常慢的算法。

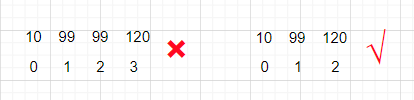
绘制表格问题

总结

• 算法的速度指的并非时间，而是操作数的增速。
• 谈论算法的速度时，我们说的是随着输入的增加，其运行时间将以什么样的速度增加。
• 算法的运行时间用大O表示法表示。
• O(log n)比O(n)快，当需要搜索的元素越多时，前者比后者快得越多。

扩展

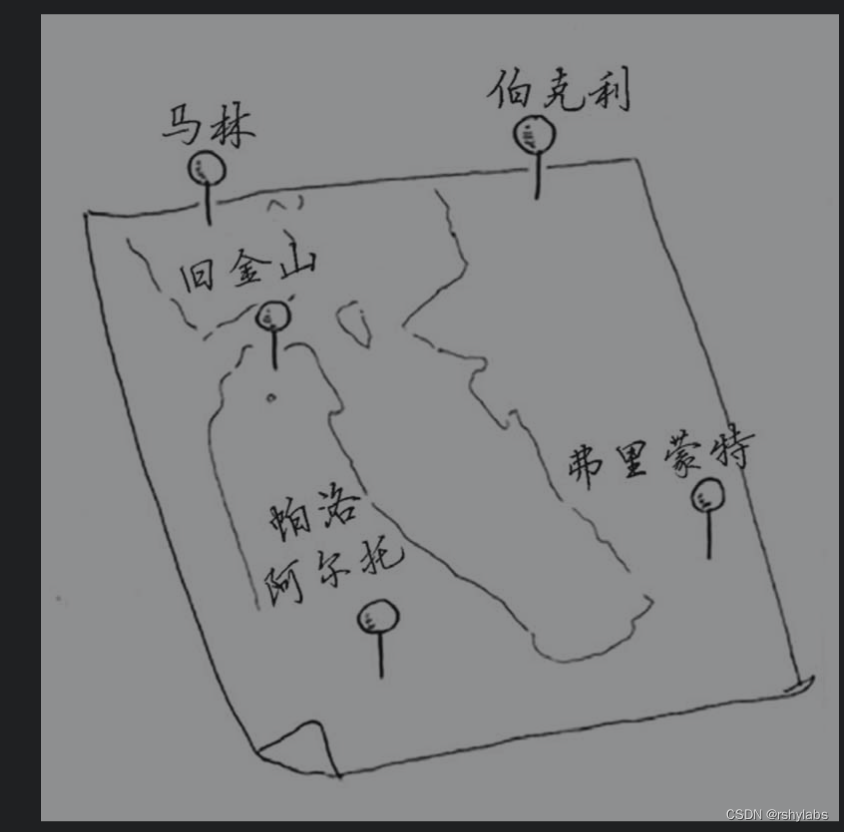
旅行商问题

一位旅行商要前往这5个城市，同时要确保旅程最短。为此，可考虑前往这些城市的各种可能顺序。对于每种顺序，他都计算总旅程，再挑选出旅程最短的路线。5个城市有120种不同的排列方式。因此，在涉及5个城市时，解决这个问题需要执行120次操作。涉及6个城市时，需要执行720次操作（有720种不同的排列方式）。推而广之，涉及n个城市时，需要执行n!（n的阶乘）次操作才能计算出结果。因此运行时间为O(n! )，即阶乘时间。