机器学习笔记之核方法——核方法思想与核函数介绍
- 引言
- 回顾:支持向量机的对偶问题
- 核方法思想介绍
- 线性可分与线性不可分
- 非线性带来高维转换
- 对偶表示带来内积
- 核函数
- 核函数的定义(2022/11/23)
- 正定核函数
引言
本节将介绍核方法以及核函数。
回顾:支持向量机的对偶问题
在支持向量机——引出对偶问题中介绍了将原问题
→
\to
→ 无约束原问题
→
\to
→ 对偶问题的转化过程。最终得到如下优化问题:
该公式位于‘西瓜书’123页最下方,详细推导过程见链接。
{
max
λ
−
1
2
[
∑
i
=
1
N
∑
j
=
1
N
λ
(
i
)
λ
(
j
)
y
(
i
)
y
(
j
)
[
x
(
i
)
]
T
x
(
j
)
]
+
∑
i
=
1
N
λ
(
i
)
s
.
t
.
{
λ
(
i
)
≥
0
∑
i
=
1
N
λ
(
i
)
y
(
i
)
=
0
\begin{cases} \mathop{\max}\limits_{\lambda} - \frac{1}{2} \left[\sum_{i=1}^N \sum_{j=1}^N \lambda^{(i)}\lambda^{(j)}y^{(i)}y^{(j)}\left[x^{(i)}\right]^Tx^{(j)}\right] + \sum_{i=1}^N \lambda^{(i)} \\ s.t. \begin{cases} \quad \lambda^{(i)} \geq 0 \\ \sum_{i=1}^N \lambda^{(i)}y^{(i)} = 0 \end{cases} \end{cases}
⎩⎪⎪⎨⎪⎪⎧λmax−21[∑i=1N∑j=1Nλ(i)λ(j)y(i)y(j)[x(i)]Tx(j)]+∑i=1Nλ(i)s.t.{λ(i)≥0∑i=1Nλ(i)y(i)=0
其中
x
(
i
)
,
x
(
j
)
(
i
,
j
=
1
,
2
,
⋯
,
N
)
x^{(i)},x^{(j)}(i,j =1,2,\cdots,N)
x(i),x(j)(i,j=1,2,⋯,N)均表示样本集合
X
\mathcal X
X的样本;
y
(
i
)
,
y
(
j
)
y^{(i)},y^{(j)}
y(i),y(j)分别表示样本
x
(
i
)
,
x
(
j
)
x^{(i)},x^{(j)}
x(i),x(j)对应的标签结果;
λ
(
i
)
,
λ
(
j
)
\lambda^{(i)},\lambda^{(j)}
λ(i),λ(j)表示样本
x
(
i
)
,
x
(
j
)
x^{(i)},x^{(j)}
x(i),x(j)对应的拉格朗日因子。
可以看出, λ ( i ) , λ ( j ) , y ( i ) , y ( j ) \lambda^{(i)},\lambda^{(j)},y^{(i)},y^{(j)} λ(i),λ(j),y(i),y(j)均表示实数,而 [ x ( i ) ] T x ( j ) \left[x^{(i)}\right]^T x^{(j)} [x(i)]Tx(j)表示两样本向量 x ( i ) , x ( j ) x^{(i)},x^{(j)} x(i),x(j)的内积结果。在线性分类任务的讨论中,我们假设样本集合 X = ( x ( 1 ) , x ( 2 ) , ⋯ , x ( N ) ) \mathcal X = (x^{(1)},x^{(2)},\cdots,x^{(N)}) X=(x(1),x(2),⋯,x(N))是线性可分的,也就是说:存在一条直线或者超平面(基于不同维度),能够将样本空间中的样本点正确划分。
但在现实任务中,样本空间中样本可能不是线性可分的。即可能并不存在一个能够将两分类样本正确划分的直线/超平面。基于这种问题,需要引入核方法思想。
核方法思想介绍
线性可分与线性不可分
线性可分是指:在二分类线性分类任务中,使用一个线性函数将样本空间中的样本正确划分。这里的正确划分指的是划分过程中不存在任何错误。常见的线性可分算法有:
- 感知机算法(Perceptron Algorithm,PLA):基于错误驱动方式,找到满足条件的参数结果。
W ^ = arg min W ∑ x ( i ) , y ( i ) ∈ D − y ( i ) ( W T x ( i ) + b ) \hat {\mathcal W} = \mathop{\arg\min}\limits_{\mathcal W} \sum_{x^{(i)},y^{(i)} \in \mathcal D} -y^{(i)}\left(\mathcal W^Tx^{(i)} + b\right) W^=Wargminx(i),y(i)∈D∑−y(i)(WTx(i)+b)
针对这种无约束优化问题,使用梯度下降方法寻找最优参数的变化方向:
W ( t + 1 ) ← W ( t ) − λ ∇ W L ( W , b ) \mathcal W^{(t+1)} \gets \mathcal W^{(t)} - \lambda \nabla_{\mathcal W}\mathcal L(\mathcal W,b) W(t+1)←W(t)−λ∇WL(W,b) - 支持向量机(Support Vector Machine,SVM)。
这里指的是硬间隔(Hard Margin) SVM算法。
相反,线性不可分是指使用线性函数进行划分时,会产生分类错误的现象。
- 图像(右)中描述的是仅存在少量错误的情况,此时使用感知机算法会导致模型无法收敛;硬间隔SVM无论如何构建直线,都无法实现线性可分:
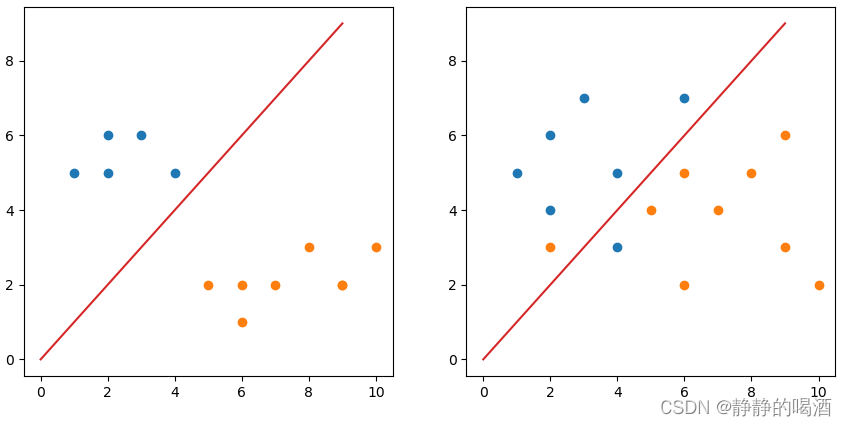
而具有代表性的解决方法有软间隔SVM:
{ min W , b 1 2 W T W + C ∑ i = 1 N ξ ( i ) s . t . { y ( i ) ( W T x ( i ) + b ) ≥ 1 − ξ ( i ) ξ ( i ) ≥ 0 \begin{cases} \mathop{\min}\limits_{\mathcal W,b} \frac{1}{2} \mathcal W^T\mathcal W + \mathcal C \sum_{i=1}^N \xi^{(i)} \\ s.t.\begin{cases} y^{(i)}\left(\mathcal W^Tx^{(i)} + b\right) \geq 1 - \xi^{(i)} \\ \xi^{(i)} \geq 0 \end{cases} \end{cases} ⎩⎪⎪⎨⎪⎪⎧W,bmin21WTW+C∑i=1Nξ(i)s.t.{y(i)(WTx(i)+b)≥1−ξ(i)ξ(i)≥0
其中:- ξ ( i ) \xi^{(i)} ξ(i)表示当前错误分类的样本点 ( x ( i ) , y ( i ) ) \left(x^{(i)},y^{(i)}\right) (x(i),y(i))到超平面 y ( i ) ( W T x ( i ) + b ) = 1 y^{(i)}\left(\mathcal W^Tx^{(i)} + b\right) = 1 y(i)(WTx(i)+b)=1的距离;
- 1 − ξ ( i ) 1 - \xi^{(i)} 1−ξ(i)表示当前错误分类的样本点 ( x ( i ) , y ( i ) ) \left(x^{(i)},y^{(i)}\right) (x(i),y(i))到分类直线 W T x ( i ) + b \mathcal W^Tx^{(i)} + b WTx(i)+b的距离。
- 不同于上述因少量误差产生的线性不可分问题,真实情况可能是样本本身就是线性不可分问题。例如:
sklearn中的make_circle样本集合。
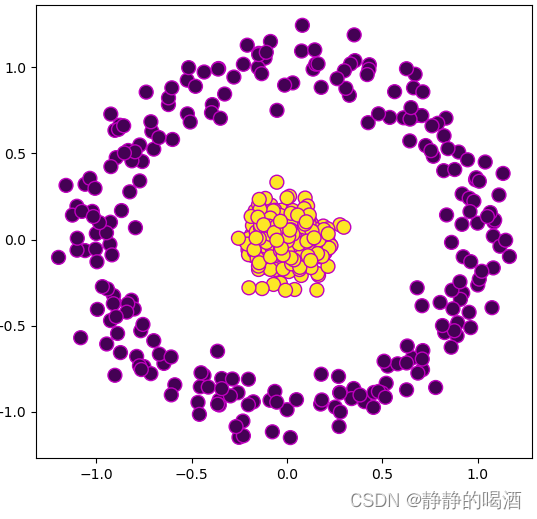
上述样本空间中的样本显然是非线性的,无法使用直线/超平面对上述两类样本进行划分。
基于上述的非线性可分问题,存在一种思路:将样本特征进行非线性转换,转换的目标是将非线性可分问题转化为线性可分问题。
非线性带来高维转换
非线性带来高维转换 的言下之意是,将当前样本空间中无法线性可分的原因归结为样本空间维度过低。以二维特征的亦或问题为例:
二维空间亦或问题图像描述如下:
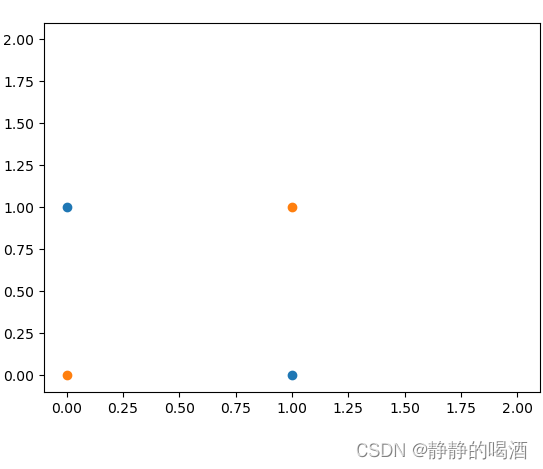
基于上图的两类样本分布(蓝色样本点(0,1),(1,0);橙色样本点(0,0),(1,1)),我们没有办法使用一条直线 对样本分类进行正确划分。
如果在当前样本特征的基础上,添加一维新的特征:
由于‘亦或问题’比较简单,可以直接将非线性转换的函数描述出来。并且这个非线性转换并不是唯一的,也可以通过其他的非线性转换方式进行描述。
x
(
i
)
=
[
x
1
(
i
)
,
x
2
(
i
)
,
(
x
1
(
i
)
−
x
2
(
i
)
)
2
]
i
=
1
,
2
,
3
,
4
x^{(i)} = \left[x_1^{(i)},x_2^{(i)},(x_1^{(i)} - x_2^{(i)})^2\right] \quad i=1,2,3,4
x(i)=[x1(i),x2(i),(x1(i)−x2(i))2]i=1,2,3,4
基于新特征的样本点表示如下:
(
0
,
0
,
0
)
,
(
0
,
1
,
1
)
,
(
1
,
0
,
1
)
,
(
1
,
1
,
0
)
(0,0,0),(0,1,1),(1,0,1),(1,1,0)
(0,0,0),(0,1,1),(1,0,1),(1,1,0)
对应三维图像表示如下:
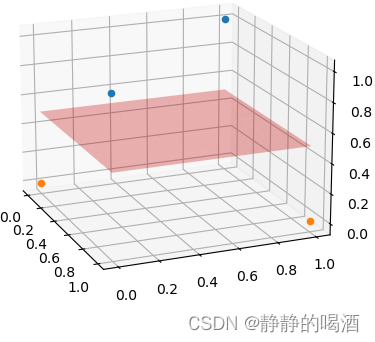
发现,原始样本点从二维特征延伸至三维特征后,很容易地找到平面对样本点进行划分。
这里引用了Cover定理(Cover Theonem)的思想:将复杂的模式分类问题非线性地投射到高维空间将比投射到地位空间更容易线性可分。
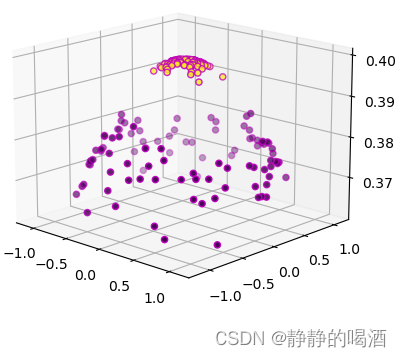
同理,我们可以尝试对上述make_circle样本集合设计相应的核函数,具体代码表示如下:
这里设计的核函数是基于高斯分布的核函数,并且两维度相互独立。非线性转换后的样本特征表示如下:
x ( i ) = [ x 1 ( i ) , x 2 ( i ) , N ( μ 1 , σ ) + N ( μ 2 , σ ) ] μ k = 1 N ∑ i = 1 N x k ( i ) k = 1 , 2 \begin{aligned} x^{(i)} & = \left[x_1^{(i)},x_2^{(i)},\mathcal N(\mu_1,\sigma) + \mathcal N(\mu_2,\sigma)\right] \\ \mu_{k} & = \frac{1}{N} \sum_{i=1}^N x_k^{(i)} \quad k=1,2 \end{aligned} x(i)μk=[x1(i),x2(i),N(μ1,σ)+N(μ2,σ)]=N1i=1∑Nxk(i)k=1,2方差σ \sigma σ作为超参数进行调整。
import matplotlib.pyplot as plt
import math
import numpy as np
from sklearn.datasets import make_circles
def kernel_function(input_space,mean,sigma):
def pdf(x,mean,sigma):
return (1 / (sigma * math.sqrt(2 * math.pi))) * math.exp(-0.5 * (((x - mean) ** 2)/(sigma ** 2)))
return np.array([pdf(i,mean,sigma) for i in input_space])
def get_new_sample(x_space,sigma):
mean_1 = np.mean(x_space[:,0])
mean_2 = np.mean(x_space[:,1])
kernel_1 = kernel_function(x_space[:,0],mean_1,sigma)
kernel_2 = kernel_function(x_space[:,1],mean_2,sigma)
kernel_space = kernel_1 + kernel_2
kernel_space = np.expand_dims(kernel_space,axis=1)
new_space = np.concatenate((x_space,kernel_space),axis=1)
return new_space
def draw_make_circle():
X_circle, Y_circle = make_circles(n_samples=200, noise=0.1, factor=0.1)
new_sample = get_new_sample(X_circle,sigma=2)
ax = plt.axes(projection="3d")
ax.scatter(new_sample[:, 0],new_sample[:, 1],new_sample[:,2],marker="o",edgecolors='m', c=Y_circle)
plt.show()
if __name__ == '__main__':
draw_make_circle()
返回图像结果如下:
对偶表示带来内积
基于非线性带来高维转换的思路,针对线性不可分问题,将样本
x
x
x的特征进行非线性转换,从而将
x
x
x特征转化为高维特征:
以数据集合
X
\mathcal X
X的某具体样本点
x
(
i
)
x^{(i)}
x(i)为例。
x
(
i
)
→
ϕ
(
x
(
i
)
)
x^{(i)} \to \phi \left(x^{(i)}\right)
x(i)→ϕ(x(i))
以支持向量机为例,因而特征空间中的划分超平面 对应模型可表示为:
f
(
x
)
=
W
T
ϕ
(
x
)
+
b
f(x) = \mathcal W^T\phi(x) + b
f(x)=WTϕ(x)+b
同理,得到的对偶问题可表示如下:
{
max
λ
−
1
2
[
∑
i
=
1
N
∑
j
=
1
N
λ
(
i
)
λ
(
j
)
y
(
i
)
y
(
j
)
[
ϕ
(
x
(
i
)
)
]
T
ϕ
(
x
(
j
)
)
]
+
∑
i
=
1
N
λ
(
i
)
s
.
t
.
{
λ
(
i
)
≥
0
∑
i
=
1
N
λ
(
i
)
y
(
i
)
=
0
\begin{cases} \mathop{\max}\limits_{\lambda} - \frac{1}{2} \left[\sum_{i=1}^N \sum_{j=1}^N \lambda^{(i)}\lambda^{(j)}y^{(i)}y^{(j)} \left[\phi \left(x^{(i)}\right)\right]^T\phi\left(x^{(j)}\right)\right] + \sum_{i=1}^N \lambda^{(i)} \\ s.t. \begin{cases} \quad \lambda^{(i)} \geq 0 \\ \sum_{i=1}^N \lambda^{(i)}y^{(i)} = 0 \end{cases} \end{cases}
⎩⎪⎪⎨⎪⎪⎧λmax−21[∑i=1N∑j=1Nλ(i)λ(j)y(i)y(j)[ϕ(x(i))]Tϕ(x(j))]+∑i=1Nλ(i)s.t.{λ(i)≥0∑i=1Nλ(i)y(i)=0
-
其中原始对偶问题中 [ x ( i ) ] T x ( j ) [x^{(i)}]^T x^{(j)} [x(i)]Tx(j)表示 x ( i ) , x ( j ) ∈ R p x^{(i)},x^{(j)} \in \mathbb R^p x(i),x(j)∈Rp自身特征的内积;
-
而 [ ϕ ( x ( i ) ) ] T ϕ ( x ( j ) ) \left[\phi \left(x^{(i)}\right)\right]^T\phi\left(x^{(j)}\right) [ϕ(x(i))]Tϕ(x(j))表示 x ( i ) , x ( j ) x^{(i)},x^{(j)} x(i),x(j)经过非线性转换得到的高维特征 的内积。
-
上面介绍的亦或例子,相比于原始特征,仅增加了一个特征;但在真实环境中,样本 x x x经过转换得到的新特征 ϕ ( x ) \phi(x) ϕ(x),其特征空间维数可能远远超过了原始特征空间的维数 p p p,甚至是 无限维。
因此,首先求解 ϕ ( x ( i ) ) , ϕ ( x ( j ) ) \phi(x^{(i)}),\phi(x^{(j)}) ϕ(x(i)),ϕ(x(j))本身计算量极高。并且还要计算 [ ϕ ( x ( i ) ) ] T ϕ ( x ( j ) ) \left[\phi \left(x^{(i)}\right)\right]^T\phi\left(x^{(j)}\right) [ϕ(x(i))]Tϕ(x(j)),从而计算量更加庞大了。
继续观察对偶问题的表达形式,实际上我们仅关心 [ ϕ ( x ( i ) ) ] T ϕ ( x ( j ) ) \left[\phi \left(x^{(i)}\right)\right]^T\phi\left(x^{(j)}\right) [ϕ(x(i))]Tϕ(x(j))内积的最终结果,而并不需要单个的 ϕ ( x ( i ) ) , ϕ ( x ( j ) ) \phi(x^{(i)}),\phi(x^{(j)}) ϕ(x(i)),ϕ(x(j))结果。因此,求解思路转化为:是否存在这样一种方法,避免求解 ϕ ( x ( i ) ) , ϕ ( x ( j ) ) \phi(x^{(i)}),\phi(x^{(j)}) ϕ(x(i)),ϕ(x(j)),从而直接求解内积 [ ϕ ( x ( i ) ) ] T ϕ ( x ( j ) ) \left[\phi \left(x^{(i)}\right)\right]^T\phi\left(x^{(j)}\right) [ϕ(x(i))]Tϕ(x(j))?
核函数(Kernal Function)的引入就是为了解决该问题。
核函数
核函数
κ
\kappa
κ的定义表示如下:
核函数被定义的核心就是避免求解
ϕ
(
x
)
\phi(x)
ϕ(x).
κ
[
x
(
i
)
,
x
(
j
)
]
=
⟨
ϕ
(
x
(
i
)
)
,
ϕ
(
x
(
j
)
)
⟩
=
[
ϕ
(
x
(
i
)
)
]
T
ϕ
(
x
(
j
)
)
\kappa\left[x^{(i)},x^{(j)}\right] = \left\langle\phi(x^{(i)}),\phi(x^{(j)})\right\rangle = \left[\phi \left(x^{(i)}\right)\right]^T\phi\left(x^{(j)}\right)
κ[x(i),x(j)]=⟨ϕ(x(i)),ϕ(x(j))⟩=[ϕ(x(i))]Tϕ(x(j))
将核函数带入,对偶问题最终可重写为:
{
max
λ
−
1
2
[
∑
i
=
1
N
∑
j
=
1
N
λ
(
i
)
λ
(
j
)
y
(
i
)
y
(
j
)
[
ϕ
(
x
(
i
)
)
]
T
ϕ
(
x
(
j
)
)
]
+
∑
i
=
1
N
λ
(
i
)
s
.
t
.
{
λ
(
i
)
≥
0
∑
i
=
1
N
λ
(
i
)
y
(
i
)
=
0
⇒
{
max
λ
−
1
2
[
∑
i
=
1
N
∑
j
=
1
N
λ
(
i
)
λ
(
j
)
y
(
i
)
y
(
j
)
κ
[
x
(
i
)
,
x
(
j
)
]
]
+
∑
i
=
1
N
λ
(
i
)
s
.
t
.
{
λ
(
i
)
≥
0
∑
i
=
1
N
λ
(
i
)
y
(
i
)
=
0
\begin{aligned} & \begin{cases} \mathop{\max}\limits_{\lambda} - \frac{1}{2} \left[\sum_{i=1}^N \sum_{j=1}^N \lambda^{(i)}\lambda^{(j)}y^{(i)}y^{(j)} \left[\phi \left(x^{(i)}\right)\right]^T\phi\left(x^{(j)}\right)\right] + \sum_{i=1}^N \lambda^{(i)} \\ s.t. \begin{cases} \quad \lambda^{(i)} \geq 0 \\ \sum_{i=1}^N \lambda^{(i)}y^{(i)} = 0 \end{cases} \end{cases} \\ \Rightarrow & \begin{cases} \mathop{\max}\limits_{\lambda} - \frac{1}{2} \left[\sum_{i=1}^N \sum_{j=1}^N \lambda^{(i)}\lambda^{(j)}y^{(i)}y^{(j)} \kappa \left[x^{(i)},x^{(j)}\right]\right] + \sum_{i=1}^N \lambda^{(i)} \\ s.t. \begin{cases} \quad \lambda^{(i)} \geq 0 \\ \sum_{i=1}^N \lambda^{(i)}y^{(i)} = 0 \end{cases} \end{cases} \end{aligned}
⇒⎩⎪⎪⎨⎪⎪⎧λmax−21[∑i=1N∑j=1Nλ(i)λ(j)y(i)y(j)[ϕ(x(i))]Tϕ(x(j))]+∑i=1Nλ(i)s.t.{λ(i)≥0∑i=1Nλ(i)y(i)=0⎩⎪⎪⎨⎪⎪⎧λmax−21[∑i=1N∑j=1Nλ(i)λ(j)y(i)y(j)κ[x(i),x(j)]]+∑i=1Nλ(i)s.t.{λ(i)≥0∑i=1Nλ(i)y(i)=0
从而对上述优化问题进行求解,得到最优模型参数
W
∗
\mathcal W^*
W∗:
支持向量机——模型参数求解传送门
W
∗
=
∑
i
=
1
N
λ
(
i
)
y
(
i
)
ϕ
(
x
(
i
)
)
\mathcal W^* = \sum_{i=1}^N \lambda^{(i)}y^{(i)}\phi(x^{(i)})
W∗=i=1∑Nλ(i)y(i)ϕ(x(i))
最终得到如下超平面模型表达式:
λ
(
i
)
,
y
(
i
)
\lambda^{(i)},y^{(i)}
λ(i),y(i)均是实数,其转置等于自身。
f
(
x
)
=
(
W
∗
)
T
ϕ
(
x
)
+
b
=
[
∑
i
=
1
N
λ
(
i
)
y
(
i
)
ϕ
(
x
(
i
)
)
]
T
ϕ
(
x
)
+
b
=
∑
i
=
1
N
λ
(
i
)
y
(
i
)
[
ϕ
(
x
(
i
)
)
]
T
ϕ
(
x
)
+
b
=
∑
i
=
1
N
λ
(
i
)
y
(
i
)
κ
(
x
,
x
(
i
)
)
+
b
\begin{aligned} f(x) & = (\mathcal W^*)^T \phi(x) + b \\ & = \left[\sum_{i=1}^N \lambda^{(i)}y^{(i)}\phi(x^{(i)})\right]^T\phi(x) + b \\ & = \sum_{i=1}^N\lambda^{(i)}y^{(i)} \left[\phi(x^{(i)})\right]^T\phi(x) + b \\ & = \sum_{i=1}^N\lambda^{(i)}y^{(i)} \kappa(x,x^{(i)}) + b \end{aligned}
f(x)=(W∗)Tϕ(x)+b=[i=1∑Nλ(i)y(i)ϕ(x(i))]Tϕ(x)+b=i=1∑Nλ(i)y(i)[ϕ(x(i))]Tϕ(x)+b=i=1∑Nλ(i)y(i)κ(x,x(i))+b
如果将核函数
κ
(
⋅
,
⋅
)
\kappa(\cdot,\cdot)
κ(⋅,⋅)找出来,上述超平面表达式中,
x
(
i
)
,
y
(
i
)
,
λ
(
i
)
x^{(i)},y^{(i)},\lambda^{(i)}
x(i),y(i),λ(i)均是已知量,它就是一个关于
x
x
x的函数。这样就避免了一个一个求解
[
ϕ
(
x
(
i
)
)
]
T
ϕ
(
x
)
\left[\phi(x^{(i)})\right]^T\phi(x)
[ϕ(x(i))]Tϕ(x)的情况。
这种‘避免求解
ϕ
(
x
(
i
)
)
,
ϕ
(
x
)
\phi(x^{(i)}),\phi(x)
ϕ(x(i)),ϕ(x)从而直接求解
[
ϕ
(
x
(
i
)
)
]
T
ϕ
(
x
)
\left[\phi(x^{(i)})\right]^T\phi(x)
[ϕ(x(i))]Tϕ(x)的思想’被称作核技巧(Kernal Trick)。
在支持向量机中,这种基于‘核函数’的展开式被称作‘支持向量展开式’(Support Vector Expansion)。
核函数的定义(2022/11/23)
首先,核(Kernal)本质上是一个映射,关于两个样本空间 相关的映射:
κ
(
x
(
i
)
,
x
(
j
)
)
\kappa(x^{(i)},x^{(j)})
κ(x(i),x(j))
其中
x
(
i
)
,
x
(
j
)
x^{(i)},x^{(j)}
x(i),x(j)均是样本集合
X
\mathcal X
X中的元素,因而满足:
x
(
i
)
,
x
(
j
)
∈
R
p
x^{(i)},x^{(j)} \in \mathbb R^p
x(i),x(j)∈Rp。
核函数的定义表示如下:
κ
:
X
×
X
→
R
∀
x
(
i
)
,
x
(
j
)
∈
X
→
κ
(
x
(
i
)
,
x
(
j
)
)
\begin{aligned} & \kappa:\mathcal X \times \mathcal X \to \mathbb R \\ & \forall x^{(i)},x^{(j)} \in \mathcal X \to \kappa(x^{(i)},x^{(j)}) \end{aligned}
κ:X×X→R∀x(i),x(j)∈X→κ(x(i),x(j))
解释一下这个定义描述了什么。
X
\mathcal X
X表示样本的特征空间,而核函数的作用在于 对两个样本的特征空间做内积,而最终的内积结果是将原始的多维特征空间映射到一维的实数域中,只要具备这种功能的函数就可以称之为核函数。
正定核函数
上述核函数的定义比较简单,我们可以根据自身需要定义核函数。例如上述两个例子的核函数:
{
κ
(
x
1
,
x
2
)
=
(
x
1
−
x
2
)
2
κ
(
x
1
,
x
2
)
=
N
(
μ
1
,
σ
)
+
N
(
μ
2
,
σ
)
\begin{cases} \kappa(x_1,x_2) = (x_1 - x_2)^2 \\ \kappa(x_1,x_2) = \mathcal N(\mu_1,\sigma) + \mathcal N(\mu_2,\sigma) \end{cases}
{κ(x1,x2)=(x1−x2)2κ(x1,x2)=N(μ1,σ)+N(μ2,σ)
而正定核函数
κ
(
x
(
i
)
,
x
(
j
)
)
\kappa(x^{(i)},x^{(j)})
κ(x(i),x(j))相比于核函数的定义,差别在于正定核函数的返回结果等价于将原始特征空间
x
(
i
)
,
x
(
j
)
x^{(i)},x^{(j)}
x(i),x(j)经过非线性转换得到的高维特征空间
ϕ
(
x
(
i
)
)
,
ϕ
(
x
(
j
)
)
\phi(x^{(i)}),\phi(x^{(j)})
ϕ(x(i)),ϕ(x(j))的内积:
这里假设'非线性转换'得到的
ϕ
(
x
(
i
)
)
,
ϕ
(
x
(
j
)
)
\phi(x^{(i)}),\phi(x^{(j)})
ϕ(x(i)),ϕ(x(j))的特征维度是
m
m
m维,核函数
κ
(
x
(
i
)
,
x
(
j
)
)
\kappa(x^{(i)},x^{(j)})
κ(x(i),x(j))的特征空间维度表示如下。
κ
(
x
(
i
)
,
x
(
j
)
)
=
⟨
ϕ
(
x
(
i
)
)
,
ϕ
(
x
(
j
)
)
⟩
=
[
ϕ
(
x
(
i
)
)
]
1
×
m
T
ϕ
(
x
(
j
)
)
m
×
1
∈
R
x
(
i
)
,
x
(
j
)
∈
X
\begin{aligned} \kappa(x^{(i)},x^{(j)}) & = \left\langle\phi(x^{(i)}),\phi(x^{(j)})\right\rangle \\ & = \left[\phi(x^{(i)})\right]^T_{1 \times m} \phi(x^{(j)})_{m \times 1} \in \mathbb R \quad x^{(i)},x^{(j)} \in \mathcal X \end{aligned}
κ(x(i),x(j))=⟨ϕ(x(i)),ϕ(x(j))⟩=[ϕ(x(i))]1×mTϕ(x(j))m×1∈Rx(i),x(j)∈X
关于正定核函数的等价定义表示如下:
κ
:
X
×
X
→
R
,
∀
x
(
i
)
,
x
(
j
)
∈
X
→
κ
(
x
(
i
)
,
x
(
j
)
)
\kappa:\mathcal X \times \mathcal X \to \mathbb R,\forall x^{(i)},x^{(j)} \in\mathcal X \to \kappa(x^{(i)},x^{(j)})
κ:X×X→R,∀x(i),x(j)∈X→κ(x(i),x(j))
如果
κ
(
x
(
i
)
,
x
(
j
)
)
\kappa(x^{(i)},x^{(j)})
κ(x(i),x(j))满足:
- 对称性: κ ( x ( i ) , x ( j ) ) = κ ( x ( j ) , x ( i ) ) \kappa(x^{(i)},x^{(j)}) = \kappa(x^{(j)},x^{(i)}) κ(x(i),x(j))=κ(x(j),x(i));
- 正定性:从样本集合
X
\mathcal X
X中任取
N
N
N个样本数据
x
(
1
)
,
⋯
,
x
(
N
)
x^{(1)},\cdots,x^{(N)}
x(1),⋯,x(N),如果对应的 “核矩阵”(Kernal Matrix)总是半正定的。其中
x
(
1
)
,
⋯
,
x
(
N
)
x^{(1)},\cdots,x^{(N)}
x(1),⋯,x(N)对应的核矩阵
K
\mathcal K
K表示如下:
K = [ κ ( x ( 1 ) , x ( 1 ) ) , κ ( x ( 1 ) , x ( 2 ) ) , ⋯ , κ ( x ( 1 ) , x ( N ) ) κ ( x ( 2 ) , x ( 1 ) ) , κ ( x ( 2 ) , x ( 2 ) ) , ⋯ , κ ( x ( 2 ) , x ( N ) ) ⋮ κ ( x ( N ) , x ( 1 ) ) , κ ( x ( N ) , x ( 2 ) ) , ⋯ , κ ( x ( N ) , x ( N ) ) ] N × N \mathcal K = \begin{bmatrix} \kappa(x^{(1)},x^{(1)}),\kappa(x^{(1)},x^{(2)}),\cdots,\kappa(x^{(1)},x^{(N)}) \\ \kappa(x^{(2)},x^{(1)}),\kappa(x^{(2)},x^{(2)}),\cdots,\kappa(x^{(2)},x^{(N)}) \\ \vdots \\ \kappa(x^{(N)},x^{(1)}),\kappa(x^{(N)},x^{(2)}),\cdots,\kappa(x^{(N)},x^{(N)}) \\ \end{bmatrix}_{N \times N} K=⎣⎢⎢⎢⎡κ(x(1),x(1)),κ(x(1),x(2)),⋯,κ(x(1),x(N))κ(x(2),x(1)),κ(x(2),x(2)),⋯,κ(x(2),x(N))⋮κ(x(N),x(1)),κ(x(N),x(2)),⋯,κ(x(N),x(N))⎦⎥⎥⎥⎤N×N
称
κ
(
x
(
i
)
,
x
(
j
)
)
\kappa(x^{(i)},x^{(j)})
κ(x(i),x(j))是正定核函数。
由于正定核函数的‘标准定义’确实很难理解,因此这里并没有去过多描述‘标准定义’,有感兴趣的小伙伴移步正定核 ——vincen 的学习笔记
下一节将介绍正定核函数的充分必要性证明。
相关参考:
机器学习-周志华著
机器学习-核方法(1)-背景介绍
机器学习-核方法(2)-正定核的两个定义
正定核 ——vincen 的学习笔记
![[附源码]java毕业设计学生宿舍管理系统设计](https://img-blog.csdnimg.cn/19ef6af27f4b4467b9e7ca2dbf988e55.png)
![[附源码]java毕业设计新生入学计算机配号系统](https://img-blog.csdnimg.cn/00c20b40dd8c402d884c23787959201f.png)