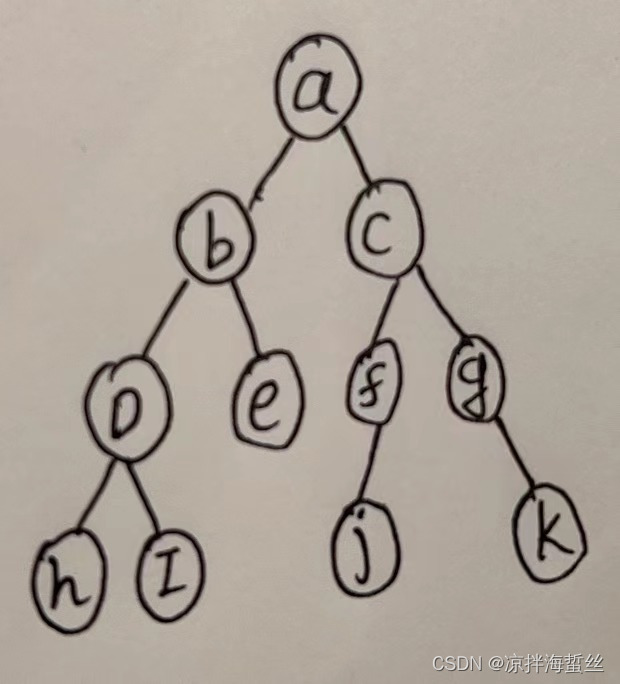
二叉树的递归遍历
递归遍历是最简单的
// 前序
class Solution {
public:
void traversal(TreeNode* cur, vector<int>& vec) {
if (cur == NULL) return;
vec.push_back(cur->val); // 中
traversal(cur->left, vec); // 左
traversal(cur->right, vec); // 右
}
vector<int> preorderTraversal(TreeNode* root) {
vector<int> result;
traversal(root, result);
return result;
}
};
// 中序
void traversal(TreeNode* cur, vector<int>& vec) {
if (cur == NULL) return;
traversal(cur->left, vec); // 左
vec.push_back(cur->val); // 中
traversal(cur->right, vec); // 右
}
// 后序
void traversal(TreeNode* cur, vector<int>& vec) {
if (cur == NULL) return;
traversal(cur->left, vec); // 左
traversal(cur->right, vec); // 右
vec.push_back(cur->val); // 中
}
二叉树的迭代遍历
实不相瞒这里我差点寄了
前序遍历
这个是最简单的,我觉得迭代法难就难在处理根节点,根节点处理不好就很容易死循环。幸好前序遍历的处理顺序就是[前 - > 左 -> 右],也就是最早可以弹出根节点,体现在程序上就是每次我们都先push进去头节点,然后记录其值,将其pop出去,然后再push进去右儿子和左儿子,这道题目就完成了
多说一嘴,我们是如何做这类迭代遍历的题目的,自然是知道答案后,模拟进栈出栈(出栈的时候就是把数值放到结果数组中的时候),得到运行的逻辑后,我们再将其用代码实现
// 前序遍历,设计算法之前,我们先找到规律
// 迭代遍历本质上就是用栈来实现遍历,而前序遍历,就是(中 -> 左 -> 右这样的顺序)
// 所以我们既然要用栈来实现这种数据结构
// 那么应该先把中间节点给push进去,然后弹出中间节点的值给vector
// 然后加入右儿子,左儿子···
// 进入下一层循环的时候,应该判断的是左儿子,此时左儿子又作为其子树的父节点,然后再次弹出···push···
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
stack<TreeNode*>st;
vector<int> res; // 首先定义一个存储结果的数组,然后我们判断当前头结点是不是空,若是空直接返回vector,若不是就将top加入到vector中然后进入下面循环中
if(root == NULL) return res;
// 刚开始的时候应该先把头结点给push进去
st.push(root);
// 然后每次进入循环都判断当前节点是不是空,若不是空就继续执行下去
// 注意每次做题的时候都要思考:我们是如何将其设计成一个循环逻辑的
while(!st.empty()) // 同时也应该保证栈不为空
{
// push元素的时候我们没有判断push进去的元素是不是空,所以要在开头加上判断
if(st.top() == NULL) {st.pop();continue; }
TreeNode* head = st.top();
int num = head -> val;
res.push_back(num);
st.pop();
// 然后把右儿子和左儿子加进来
st.push(head -> right);
st.push(head -> left);
}
return res;
}
};
中序遍历
中序遍历就有一些麻烦了,用孙哥的话讲就是:遍历的顺序和记录的顺序不一样
做题之前我们先模拟好进栈和出栈的情形:
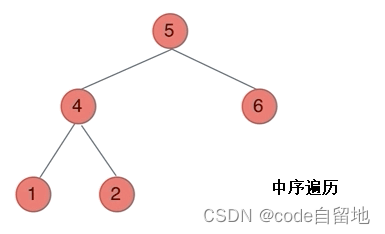
因为是中序遍历,所以开始的时候是元素1出栈,那么岂不是意味着元素1是最后进栈的?肯定不是
一步步来,我们刚开始拿到的是元素5,也就是根节点,然后去搜元素5的左儿子走到元素4处,再搜索元素4的左儿子···这显然是一个循环啊,那么什么时候停止呢?“当前节点为空”。因为我们整个的迭代遍历都是用while循环去实现的,实际上我们在把当前节点的左儿子push进栈之后,就应该定位到左儿子了,所以“当前节点为空”实际上是在下一个循环中去判断了。那么“当前节点为空”后,我们又要执行什么操作呢?此时我们已经搜到应该输出的第一个节点的左儿子了,注意不是上图中的元素1,而是1的左儿子,1的左儿子是空,我们才会进行如下的操作——那么既然已经是空指针了,就一定要pop出去,然后此时栈口就是元素1,我们也一定是要pop的(pop的同时也会在数组中记录这个值),pop之后呢?再寻找其父节点吗?不是的,应该把1的右儿子push进去,如果不理解的话可以看元素4——当1的左右儿子都pop出去后,1早就pop出去了,自然此时的元素应该是4,那么按照我们上面的流程,应该也要把4给pop出去,此时还有元素2呢!所以我们把1pop出去后,应该寻找其右儿子···这一套逻辑就已经梳理完毕了
// 接下来我们考虑迭代遍历,中序遍历中是有类似于(回溯)的操作的,所以比前序遍历要麻烦一点
// 其实主要是父节点的问题,很容易造成死循环,因为刚开始我们是一直往左下方走的,遍历完毕之后肯定要往上,如果处理不当肯定就会造成死循环(在前序遍历中刚刚push进去中间结点就pop了所以死循环的问题并不明显)
// 因此我们的while循环中肯定是有两套逻辑的,第一套逻辑是往左下方走的逻辑,第二套逻辑是往上回溯的,往上回溯的话,当前节点一定要往右下方走,并且走之前中间节点一定要pop掉,所以就很清晰了
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
vector<int> res;
stack<TreeNode*> st;
if (root == NULL) return res;
// 刚开始的时候把根节点加入到栈中
st.push(root);
// 注意弹出的顺序就是数字加入vector中的顺序
// 什么时候终止循环?自然是整个栈都为空的时候
while (!st.empty())
{
if (st.top() == NULL) // 按照我们的写法,在else中肯定是会push进入空节点的,所以空节点肯定是要pop的,至于pop后,栈内的就是其父节点了,但是可能一开始pop的就是根节点,所以我们要加上判断
{
st.pop(); // 空节点肯定是要pop出去的
if (!st.empty()) // 若是当前栈内不空
{
TreeNode *cur = st.top();
st.pop(); // 这里pop的是空节点的父节点
res.push_back(cur->val); // 将父节点的值加入到res中
st.push(cur->right); // 然后加入右边子树
}
}
//如果当前节点不空,那么我们就去搜其左子树
else
{
TreeNode *cur = st.top();
st.push(cur->left); // 这个操作一定是会push进去空节点的
}
}
return res;
}
};
后序遍历
后序遍历要是按照前面的逻辑来考虑——用进栈出栈顺序来模拟,就非常非常麻烦

按照后序遍历的方式,那么应该是先弹出左右儿子后才弹出父节点,那么我们在最外侧的while循环内要写的if-else逻辑就会非常麻烦,之前的情况都是”要么头节点先弹出,要么头节点跟着子节点弹出“,所以逻辑都比较简单,但是显然后序遍历中即使左右儿子都弹出,父节点也不一定会马上弹出——不弹出就会死循环。所以while中的代码逻辑会很复杂
孙哥牛逼,孙哥交换了下前序遍历中左右节点弹出的顺序,然后最后reverse了下输出数组,就得到了后序遍历
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
stack<TreeNode*>st;
vector<int> res;
if(root == NULL) return res;
st.push(root);
while(!st.empty())
{
if(st.top() == NULL) {st.pop();continue; }
TreeNode* head = st.top();
int num = head -> val;
res.push_back(num);
st.pop();
st.push(head -> left); // 相比前序遍历交换了这行和下一行
st.push(head -> right);
}
reverse(res.begin(),res.end()); // 数组翻转
return res;
}
};
二叉树的统一迭代法
统一迭代法的思路也很牛,我们之前写中序遍历的迭代法的时候就应该明白了:当我们遍历到空指针的时候,就是转换逻辑的时候
那么我们想用一套差不多的思路同时实现前中后序遍历,就应该消除空指针后转换逻辑的写法
换言之,所有的输出前都应该有NULL(因为要统一)
那么按照这个思路,我们化整为零,将所有的节点的处理方式都统一化——遍历到当前节点的时候,若当前节点不为空,就将当前节点pop出去,再将其左儿子(不为空)和右儿子(不为空)和自己(后面加上NULL)加进来,加入的顺序就参考前中后序遍历的顺序;若当前节点为空,那么就pop并且将其值加入到数组中去。多一句嘴,为什么左儿子和右儿子后不加上NULL,只有自己后面加上NULL?因为开头说了,每个节点只有在遍历到自己的时候才会处理,处理后才会在自己后面加上NULL。
//中序遍历
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
vector<int> result;
stack<TreeNode*> st;
if (root != NULL) st.push(root);
while (!st.empty()) {
TreeNode* node = st.top();
if (node != NULL) {
st.pop(); // 将该节点弹出,避免重复操作,下面再将右中左节点添加到栈中
if (node->right) st.push(node->right); // 添加右节点(空节点不入栈)
st.push(node); // 添加中节点
st.push(NULL); // 中节点访问过,但是还没有处理,加入空节点做为标记。
if (node->left) st.push(node->left); // 添加左节点(空节点不入栈)
//后序遍历就将中间节点第一个入栈
//前序遍历就将左儿子第二个入栈
} else { // 只有遇到空节点的时候,才将下一个节点放进结果集
st.pop(); // 将空节点弹出
node = st.top(); // 重新取出栈中元素
st.pop();
result.push_back(node->val); // 加入到结果集
}
}
return result;
}
};
二叉树层序遍历
Leecode 102. 二叉树的层序遍历
还是蛮简单的,后面打10个也太秀了,倒不如说···题太水了
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
vector<int> result;
stack<TreeNode*> st;
if (root != NULL) st.push(root);
while (!st.empty()) {
TreeNode* node = st.top();
if (node != NULL) {
st.pop();
if (node->right) st.push(node->right); // 右
if (node->left) st.push(node->left); // 左
st.push(node); // 中
st.push(NULL);
} else {
st.pop();
node = st.top();
st.pop();
result.push_back(node->val);
}
}
return result;
}
};
Leecode 107. 二叉树的层序遍历 II
直接输出reverse,这也···
class Solution {
public:
vector<vector<int>> levelOrderBottom(TreeNode* root) {
// 用之前的板子,然后用一个新的vector来倒序接受就是了
vector<vector<int>> res;
queue<TreeNode*> que;
if(root != NULL) que.push(root);
while(!que.empty())
{
vector<int> cube;
int size = que.size();
// 因为我们要循环遍历数组,然后取出其中的元素将其值加入到一维vector中,并且将其左儿子和右儿子都加入到队列中
for(int i=0;i<size;i++)
{
TreeNode* head = que.front();
cube.push_back(head -> val);
que.pop();
// 一定要注意左右儿子,只有它们不为空的时候才可以push进去
if(head -> left) que.push(head -> left);
if(head -> right) que.push(head -> right);
}
res.push_back(cube);
}
reverse(res.begin(), res.end()); // reverse居然还可以改变数组的顺序
return res;
}
};
Leecode199 .二叉树的右视图
仔细理解题意,其实我们只要把二维数组中的最后一个元素加入到新的数组中输出就行了,但是因为每次我们都用一维数组记录一层的值,因此每层遍历完后我们直接记录最后一个值即可
class Solution {
public:
vector<int> rightSideView(TreeNode* root) {
vector<int> res;
queue<TreeNode*> que;
if(root != NULL) que.push(root);
while(!que.empty())
{
vector<int> cube;
int size = que.size();
// 因为我们要循环遍历数组,然后取出其中的元素将其值加入到一维vector中,并且将其左儿子和右儿子都加入到队列中
for(int i=0;i<size;i++)
{
TreeNode* head = que.front();
cube.push_back(head -> val);
que.pop();
// 一定要注意左右儿子,只有它们不为空的时候才可以push进去
if(head -> left) que.push(head -> left);
if(head -> right) que.push(head -> right);
}
int num = cube[cube.size()-1];
res.push_back(num);
}
return res;
}
};
明天接着打十个···笑死


![[附源码]java毕业设计学生档案管理系统论文](https://img-blog.csdnimg.cn/42ea0a00da824fda99ca7741f084ce8d.png)