目录

1.算法概述

2.仿真效果预览

3.MATLAB部分代码预览

4.完整MATLAB程序

---

1.算法概述

内容： N个天线按等距分布在z轴上，第N个和第N-1的之间的天线的距离是一定的为d。

在上述有红色的一块，是计算Taylor 公式的，有一个疑问就是，我能否直接调用pos 的function 和phase weight 只需在之后多乘以一个w（i）, 我试验过总是出错，希望能够帮忙改正；

四种方法：

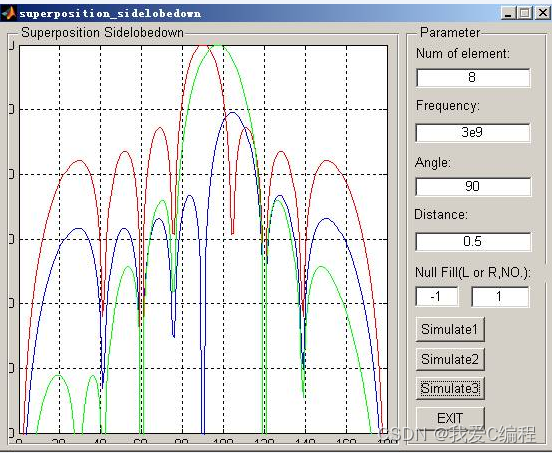
superposition+sidelobedown (变量 m 控制第几个null filling，amplitude)

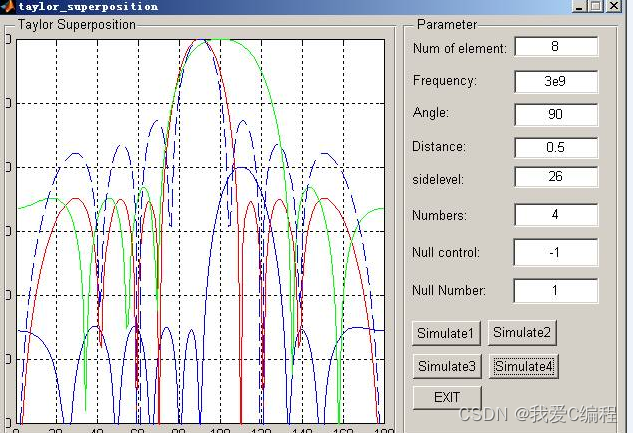
taylor+superposition( imp: 1是左边的null -1还是右边的null，sidelevel，null（）第几个null filling， amplitude）

Chebwin+superposition（m:第几个null filling，flag:1是左边的null，-1是右边的null， sidelevel，amplitude）

Chebwin+Taylor （chebwin sideleve，Taylor sidelevel）

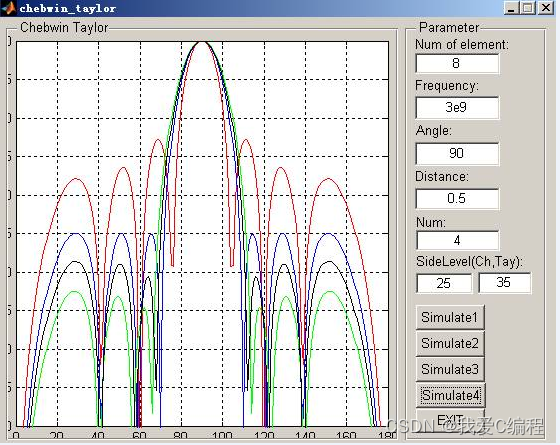
2.仿真效果预览

matlab2022a仿真结果如下：

 

 

 

3.MATLAB部分代码预览

function normalized_y = func_Chebwin_supersition_sub1(N,f,b_angle,pos,sidelevel);
 
Phaseweight  = zeros(1,180);
w            = chebwin(N,sidelevel);
for t=1:1:180
    temp       = zeros(1,N);  
    total_temp = zeros(1,N);
    for i=1:N
        belta         = calculate_weights(f,N,-1,b_angle,pos(i));
        weight        = calculate_weights(f,N, 1,t      ,pos(i)); 
        total_temp(i) = real(w(i)*(weight.*belta));
    end
    Phaseweight(t)=sum(total_temp);
end
 
y            = Phaseweight;
ymax         = max(abs(y/0.1));
normalized_y = abs(y)/ymax;
01_052_m

4.完整MATLAB程序

matlab源码说明_我爱C编程的博客-CSDN博客

V