图的概念:图的数据结构由两个集合构成,一个是顶点集V (vertex),一个是边集E(Edge);无向图一般记为G(V , E) ;有向图记为 G<V, E>
有向图就是边的指向是有方向区分的,例如从A->B ;从A可以到B,但是B不能到A(有向图的边是一个箭头,称之为弧,弧头是w,弧尾是v)
无向图的边是无方向区分的,只要A-B,从A可以到B,从B也可以到A
重要概念如下:
1:图一定不可以是空图,也就是说顶点集一定不能为空,边集可以为空
2:完全图:若任意两个顶点之间都存在着边(注意这里的边是任意两个顶点直接相连的边),则称该图是完全图。
无向完全图有n*(n-1) / 2 条边。
有向完全图有n*(n-1) 条边
3:子图:图中的某一部分顶点和一部分与顶点相连的边构成的新图,即是子图。(注意一定不能是简单的说“边的子集”和“顶点的子集”,必须是与顶点相连的边才可以构成子图)
针对无向图来说,超级重要的概念有:
4:连通:若从顶点A到顶点B有路径存在,则称AB是连通的
5:连通图和非连通图:如果图中任意两个顶点都有路径存在(不一定是直接相连的路径,这里注意跟完全图概念区分),则称该图为连通图,其实也就是字面意思“整张图是连通的”,如果有某些顶点与其它顶点并不连通,即某些顶点时孤立的,则称为非连通图。
6:连通分量(也称极大连通子图):一张图G中假如有ABC连通,DE连通,则称之有两个连通分量,即两个极大连通子图(也就是图G中,连通的子图)。
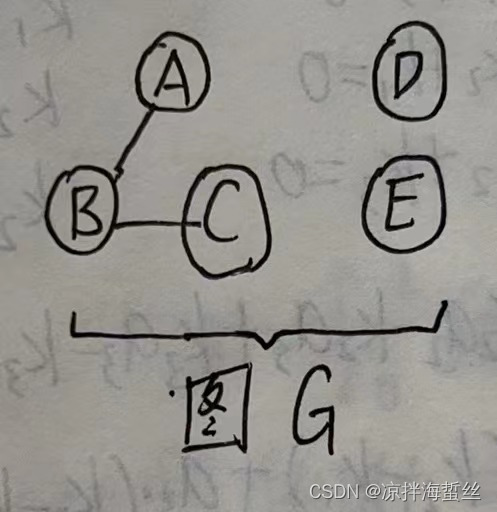
(7)对于无向图来说,N个顶点,至少需要N-1条边,才能形成连通图(画图好理解),如果N个顶点需要构成完全图,最少需要n*(n-1)/2条边。
如果边数小于n-1,则该图肯定是非连通图。
针对有向图来说,超级重要的概念有:
8:强连通:这个概念跟无向图的连通一定要区分,因为有向图是有向的,所以它的连通一定是“更强”的连通,所以记强连通。若AB强连通,则一定要有A->B 以及 A<- B;也就是两个方向都必须有,才能称为强连通。
9:强连通图:若有向图G中,图中任意两个顶点都有路径存在(不需要直接连接的路径,可以经过N个顶点,只要能有路径),则图G是强连通图
10:强连通分量(也称极大强连通子图):跟无向图连通分量的概念一定要区分,强连通分量是指子图中一定要存在环,所以判断一个有向图是否存在强连通分量,一定要去找环,如果无环,证明最后一个顶点D无法回溯到第一个顶点A,也就是D到A没有路径,那么就不是强连通的。
11:对于有向图来说,N个顶点的有向图,最少最少需要n条边(构成一个环),才能构成强连通图。要构成有向完全图(有向完全图一定是强连通图,任意顶点都有来回两个箭头路径),则需要n*(n-1)条边。
极大连通子图和极小连通子图:
12:都是针对无向图的说法,极大和极小的区别,就在于极大必须包含该子图的所有的边,也就是说不单止要连通,还要保留全部边。极小连通子图只需要保留保证图连通的最少的边数,也就是说能连通就行。
注意⚠️:生成树是极小连通子图,生成树不是极大连通子图(因为不会包含所有边),所以生成树当然就不是连通分量
稠密图和稀疏图:
13:稠密和稀疏是针对边来说的,边数多就是稠密,边数少就是稀疏。(想像成渔网,边数多,整张网就很密,边数少,整张网就很稀疏)
图的例题:
(1)N个顶点N条边的无向图,一定是有环的(画图可以发现,若每个顶点都有一条边,则一定有环);但是注意有环不一定连通,是否连通还要看边数(若n个结点的无向图有n*(n-1)/2条边,则一定一定是完全图,完全图一定是连通的且有环的)和从某个顶点进行深搜或者广搜是否可以遍历整张图。
(2)图的遍历并不是单纯的从某个顶点出发遍历其余顶点。因为图有可能是非连通的,单纯从某个顶点开始,只能遍历某张子图,其余子图中的顶点是遍历不到的,所以要遍历图,必须循环遍历顶点集V,遍历过的顶点打上标记,若一次遍历完成之后还有某些顶点未被打上遍历标记的,则开始下一轮循环,直到把顶点集V所有的顶点都打上遍历标记(此时的子图中的顶点也已被遍历),才算是一次完整的图的遍历。
(3)一个有28条边的非连通无向图至少有()个顶点
分析:有28条边还非连通,要求顶点最少,要让顶点最少,耗费边数还要多,那肯定就是完全图这个败家子,则看看28条边能构成多少个顶点的无向完全图,代入公式:N*(N-1) / 2 = 28 ; 解得N = 8 ;8个顶点用28条边构成了一个完全无向图,但是题目要非连通,那就再加一个孤立的顶点,9个顶点即可。类似题目很多,但是都是考无向有向图的完全图的边数公式而已。
(4)【2010】若无向图G(V ,E) 中含有7个顶点,保证图G在任何情况下都是连通的,则最少需要(16)条边
因为它有7个顶点,还要保证任何情况都连通,那么只能看它添了多少条边的时候,再添一条边一定连通,也就是先让它6个顶点构成无向完全图,消耗掉 6 * (6-1) / 2 = 15 条边,然后再 + 1 = 16,这样它就一定会跟第七个顶点相连通了。这样图G的一定一定能保证是连通图。因为15条边已经把6个顶点塞饱了,它们已经没地方再加一条边了,只能跟第七个顶点发生关系,一发生关系,马上构成连通图。
具有6个顶点的无向图,当有()条边时,可以确保是一个连通图
这题跟上一题完全一样的思路,6个顶点无向图,先塞饱5个顶点,用 5*(5-1)/2 = 10 条边,此时再+1条边= 11,一定会跟第六个顶点发生关系,构成连通图
(5)图G有n个顶点,若是连通无向图,边的个数至少是:
根据公式,只要保证连通,n个顶点的无向图只需要n-1条边
若是强连通有向图,边的个数至少是:
根据公式,要保证强连通,n个顶点必须要用n条边绕一个环
(6)无向图G有23条边,度为4的顶点有5个,度为3的顶点有4个,其余都是度为2的顶点,则图G一共有多少个顶点?
分析:
一条边能贡献两个度,则一共46个度,度为4的有5个顶点,则消耗了20个度;度为3的4个顶点消耗了12个度;剩余 46 - 12-20 = 14;题目又说其余都是度为2的,则14 / 2 = 7 ;即有7个度为2的顶点,图G则一共有 7 + 5 + 4 = 16 个顶点
(7)若一个具有n个顶点,e条边的无向图是一个森林,则该森林必有()棵树
这道题也是王道的,一般这种题都是特值法,取一个非常极端但是又合理的例子(例如度为3的树,有10086个结点,问树深度高度,直接用10083个做结点叠层数,最后3个做叶子结点这种变态例子)
思路一:这里我们假设森林有x棵树,那么我要用x-1条边,就可以连成一棵新的生树,但是原本这x棵树里面又有e条边,所以这棵新的树一共有x-1+e条边。根据树的性质,除了根结点没边连着它,其余每个结点都至少有一条边指向它,所以 总结点数 = 总边数 + 1
也就是 n = (x-1+e) + 1
x = n-e
思路二:例如我假设e条边每一条边都连接着两个顶点,构成一棵树,那么就消耗了2e个顶点组成了e棵树,剩下的顶点自己孤零零构成一棵没有边的树,也就是剩下:n - 2e个顶点,一共 n - 2e 棵树;
那么一共有 : n-2e+e = n - e 棵树
(8)【2017】已知无向图G含有16条边,度为4的顶点有3个,度为3的顶点有4个,其它顶点的度小于3,则图G中所含的顶点个数至少是()
分析:
16条边奉献32个度,度4有3个,消耗12度;度3有4个,消耗12个度;则剩余:32 - 12 -12 = 8 度
;剩余可能有度1度2的顶点,但是题目要所包含的顶点数至少,也就是最少最少可以允许只有多少个顶点,那我肯定选择度为2,这样一个顶点消耗2度,能尽快消耗完剩余的度数。8 / 2 = 4 ;也就是只需要再用4个度为2的顶点即可。
则总顶点一共有:
3 + 4 + 4 = 11 个
图的存储
邻接矩阵法(适合稠密图):
typedef struct {
char v[100];
int e[100][100];
} Graph;
邻接矩阵法存储无向图时,一定是一个对称矩阵,因为它不分出度还是入度,既然是对称矩阵,所以它又支持压缩存储,即只存储上三角或者下三角部分,所以在稠密图的应用中,它有非常好的效果。
它的具体存储方式如下:
针对一张4个顶点的无向图
(1)假设有ABCD个顶点,则生成一个4*4的方阵,行和列都是ABCD,然后依次从第一行第一列开始填01(有边1,无边0)
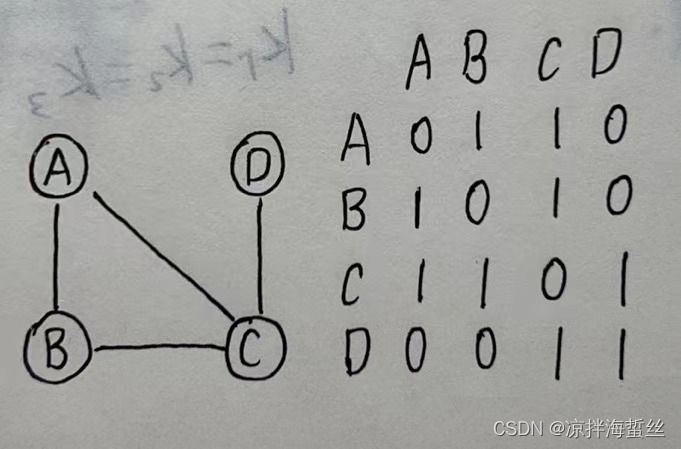
这个矩阵由于次数是1,所以代表着从某点到某点,路径长度为1的路线有多少条,那么可以很清楚看到,从A到A的长度为1的零条,A到B一条,B到C一条
(2)若在这个矩阵基础上,再乘以自身,得到矩阵的平方,平方次数是2,则代表着从某点到某点,路径长度为2的路线有多少条:

例如从矩阵上反映,从A到A路径长度为2的有2条,这两条分别是 【A】【B】(左边矩阵第一行第二列)乘以 【B】【A】(右边矩阵第二列第一行)+【A】【C】 乘以【C】【A】 = 2。也就代表着 这两条路线是:从A到B,再从B回到A;或者从A到C,再从C回到A;
是不是很神奇,再举一个例子:新矩阵从C到C的路径长度为2的路线有3条,分别是:
【C】【A】乘以【A】【C】 + 【C】【B】乘以【B】【C】 + 【C】【D】乘以【D】【C】 = 3
也就是说,从C到A再从A回到C
从C到B再从B回到C
从C到D再从D回到C
完美把路线和路线条数都展示出来了。
(3)如果再平方基础上再乘以自身,形成立方的矩阵,则代表着从某点到某点的,路径长度为3的路线有多少条,分别怎么走,都会明明白白:
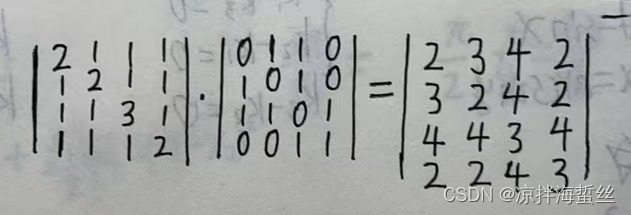
基于路径长度为2的基础上,从A到C点的路径长度为3的路线有4条,分别是:
(1)【A】【A】乘以【A】【C】 + (2)【A】【B】乘以【B】【C】 + (3)【A】【D】乘以【D】【C】 = 4
左边矩阵是平方基础上得来的,所以要看回平方时候的路线图:
代表着4条路径长度为3的路径分别为:
(1)
其中【A】【A】是矩阵平方时候产生的路径【A】【B】乘以 【B】【A】+【A】【C】 乘以【C】【A】 = 2
从A到B,再从B回到A,再从A出发到C
从A到C,再从C回到A,再从A出发到C
(2)
【A】【B】是矩阵平方时候产生的路径【A】【C】乘以 【C】【B】= 1
从A到C,再从C到B,再从B到C
(3)
【A】【D】是矩阵平方时候产生的路径【A】【C】乘以 【C】【D】= 1
从A到C,再从C到D,最后从D回到C
虽然这样绕来绕去看起来好像很傻,但是它确确实实能为我们指明一条路是从某点通往某点的,如果不想走回头路,可以再加其它业务逻辑去筛掉即可。这个作用还是很强大的。
邻接矩阵存储有向图:
有向图用1表示出度,也就是指出去的对应下标为1,入度为0(很好理解,因为这里1表示的是此路可通行,而有向图的入度对于当前顶点来说是不可通行的,相当于没路,所以也就是0,只有出度,可通行,为1)
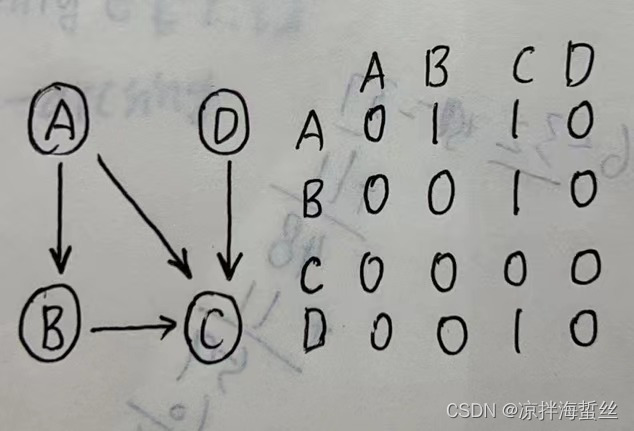
这里也是指的路径长度为1的,如果要看路径长度为2的,也可以做该矩阵的平方,跟无向图是一个玩法
优点:
直观,方便简单,易于编码实现。
如果是存储稠密图,如果是无向图配合上下三角矩阵转一维数组的压缩方式,可以节省很多空间。
缺点:
效率相对很低,计算量很大,中间结果存储会占用很大内存空间。
由于矩阵固定是n*n方阵,如果是稀疏图,会产生很多不必要的空的存储空间。
如果要在邻接矩阵中删除某个结点,则需要遍历,时间复杂度O(n)
邻接表法
为了更高效更方便存储稀疏矩阵,于是有了邻接表法,它利用数组+链表的存储方式(类似于哈希表),给每一个顶点分配一个数组下标位置,同时把与该顶点相连的顶点的数组下标链接在结点后面。
// 边表结点
typedef struct ArcNode{
int index; // 该边指向的顶点的数组下标
struct ArcNode *next; //下一个边表结点的指针
} ArcNode;
// 顶点表结点
typedef struct VNode{
char data; // 顶点信息,存储例如:ABCD,1234之类的值
ArcNode *next; // 链接第一个边表结点
} AdjList[100];
// 邻接表结构
typedef struct {
AdjList[100];
int vexnum; arcnum; // 顶点数和弧数
} ALGraph
如果是无向图,则一条边会同时存在于两个边表结点;如果针对有向图,则是只记录出边,一条边只会存在于一个边表结点
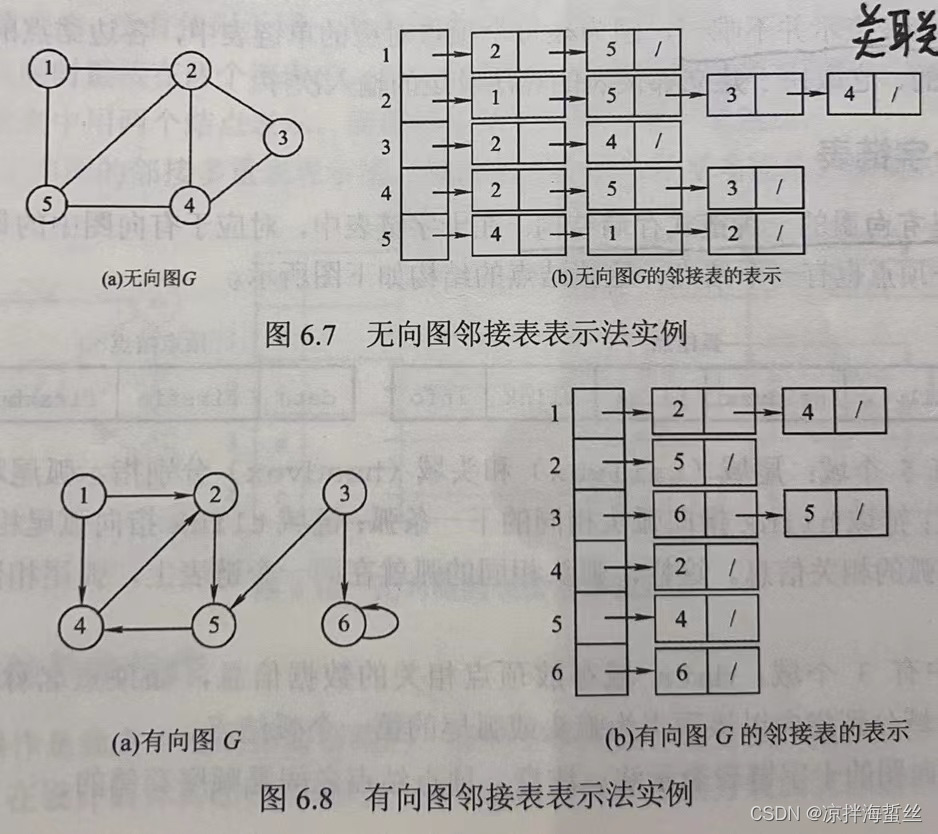
(本图摘自王道数据结构)
如果是用邻接表存储无向图,则边表结点一定是偶数个;如果是奇数个边表结点,那么一定是有向图。
例题:
(1)n个顶点的无向图的邻接表最多有(n*(n-1))个边表结点
分析:n个顶点的无向图,如果是完全图,则边最多,最多有 n*(n-1) / 2 条边,每条边都会产生两个边表结点,所以最多会有 n*(n-1) 个边表结点。
(2)假设有n个顶点,e条边的有向图用邻接表表示,则删除与某个顶点v相关的所有边的时间复杂度是:O(n+e)
分析:
要删除某个顶点的所有边,则要循环找到对应顶点v,然后依次删除它的出边表,此时关于顶点v的出边就全部删掉了,因为出边表最多有n-1个,也就是假设v对其它所有顶点都有出边
在上面循环中,还要删除它的入边,删除入边首先遍历顶点表结点O(n),逐个找除了V以外的顶点表结点的出边表链接O(e),删除与V相关的出边,这样V的入边也会消失了、
总的复杂度是O(n+e)
(3)【2021】已知无向连通图G由顶点集V和边集E组成,|E|>0,当G中度为奇数的顶点个数为不大于2的偶数时,G存在包含所有边且长度为|E|的路径(称为EL)路径(图G采用邻接矩阵存储)
(1)设计算法,判断G是否存在EL路径,如果存在,返回1,否则返回0;给出算法的基本思想
(说实话,当时看题目描述的什么度为奇数的顶点个数为不大于2的偶数,就包含EL路径。这一段卡了好久没想懂,根本搞不懂它要求什么,后来也是看了解析才知道我们只需要统计度为奇数顶点个数即可,看它是不是0或者2即可,不用管它什么鸡毛EL路径)
既然使用邻接矩阵,那我外层循环只需要从第一行遍历到最后一行,内存循环从第一列遍历到最后一列,每一行就是一个顶点的出入度信息,为1则++ ,最后拿它的度判断%2是否=0,如果是,证明当前顶点是偶数,如果不是,证明当前顶点的度是奇数,奇数顶点sum++;
最后看sum是不是0或者2,是则有EL路径,不是则没有。
(2)代码
(3)说明所设计算法的时间复杂度和空间复杂度
由于邻接矩阵是n*n的方阵,循环耗费O(n^2);空间复杂度O(1)
图的遍历:
深度优先 BFS(专注地一条路走到底,走到无路可走,再回头选其他路)
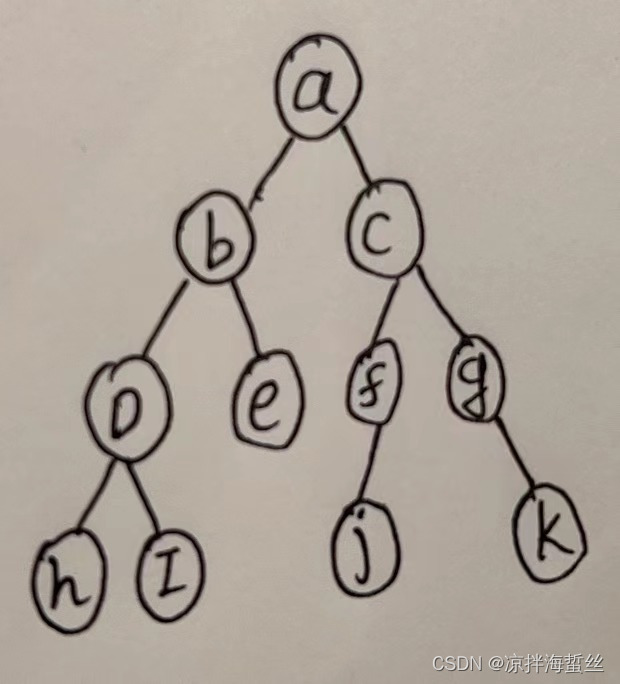
过程:
初始化一个辅助队列
(1)假设从根结点a开始,相连有b,c结点,则先把a入队,然后把a出队,然后把b, c 入队
(2)b出队,把b临近的d e 入队;c 出队,把c临近的fg入队
(3)d 出队,hi入队,e出队,啥都没入队,f出队,j入队,g出队,k入队
(4)hi出队,jk出队
(5)深度搜索完成
由于借助了一个辅助数组,大小一般设定为顶点个数,空间复杂度O(V)
当使用邻接表存储时:
搜索顶点的连接点,是顺着边摸索过去的,所以肯定是每条边都遍历一边,时间复杂度是O(E)
当使用邻接矩阵存储时:
由于N*N 个顶点的方阵、时间复杂度也就是O(V^2) 次
根据广度优先可以产生一棵树,称之为广度优先生成树,但是广度优先生成树并不唯一
广度优先 DFS(由近至远,每次都往每一个方向迈一步)
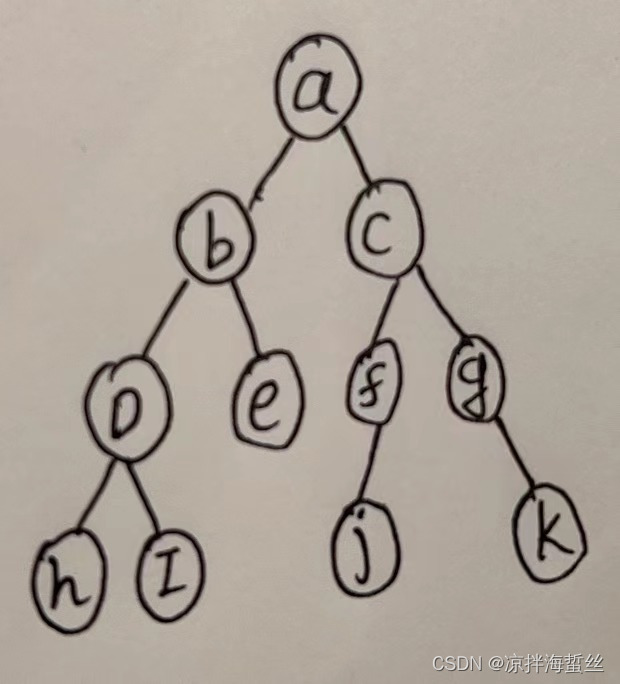
深度搜索一般通过递归的方式进行
(1)从a开始,先找b,b到d,d到h,第一条路走到头了,退回d
(2)d到i,第二条路也到头了,退回d,d发现这条路都走过了,退回b
(3)b到e,到头了,退回b,b发现路都走过了,退回a
(4)a到c。。。。。。
(5) 继续1~4的步骤,直到把所有的路都走完,这就是深度优先搜索
有多少个顶点,就会递归多少次,递归使用的递归工作栈,所以空间复杂度是O(V)
当使用邻接表存储时:
时间复杂度为O(V + E) ;
当使用邻接矩阵存储时:
由于N*N 个顶点的方阵、时间复杂度也就是O(V^2) 次