1.算法概述

4进制的DPSK通常记为DQPSK。DQPSK信号编码方式如下表：

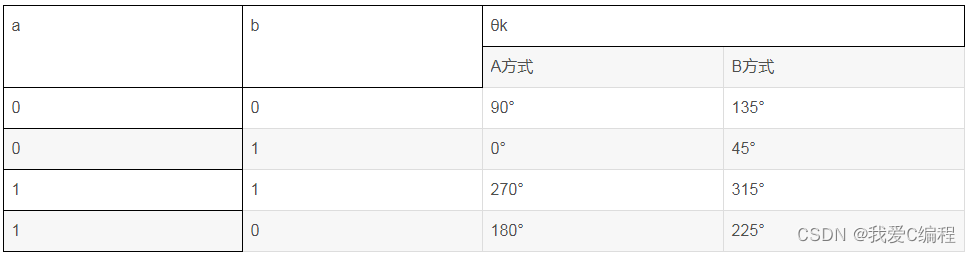
表中 θk是相对于前一相邻码元的相位变化。共有A、B两种方式。B方式中相邻码元间总有相位改变，故有利于在接收端提取码元同步。另外由于其相邻码元相位的最大相移为±135°，比A方式的最大相移小，素在通过频带受限的系统传输后其振幅起伏也较小。B方式DQPSK又称π/4DQPSK。DQPSK的产生方法与QPSk类似，但是DQPSK先将输入的双比特码经码型变换，再用码型变换器输出的双比特码进行四相绝对移相，则所得到的输出信号就是四相相对移相信号。通常采用的方法是码变换加调相法和码变换加相位选择法。

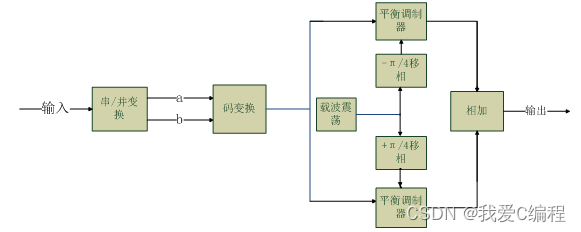
码变换加调相法。码变换加调相法产生DQPSK信号的组成方框图如下图所示。串行的二进制不归零双极性码元经串并转换器变换后变为两路并行码元ab，经码变换器变换为相对码元cd，之后分别与一对相干载波相乘，最后进行相加，即可产生DQPSK信号。与QPSK信号的产生方法不同的是，DQPSK的产生需将串并转换后的码元ab经码变换器变为相对码cd，且在相干载波的产生时，用两个π/4相移器代替一个π/2相移器，这样所产生的码元符合A方式编码。

码变换加相位选择法。其组成方框图如下图所示。其中的逻辑选项电路除按规定完成选择载波的相位外，还应实现将绝对码转换成相对码的功能。也就是说，在四相绝对移相时，直接用输入双比特码去选择载波的相位；而在四相相对移相时，需要将输入的双比特码ab转换成相对应的双比特码cd，再用cd去选择载波的相位，这样就可产生DQPSK信号。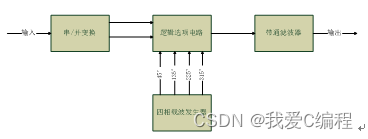

2、DQPSK信号的解调

DQPSK信号的解调与2DPSK信号的解调类似，也有两种方法，分别是极性比较法和相位比较法。

极性比较法。其原理方框图如下图所示。由于DQPSK信号可以看做是两路2DPSK信号的合成，解调时也可以分别按两路2DPSK信号解调，因此在解调过程中用两路相干载波去解调，可以很容易分离出这两路正交的2DPSK信号。经低通滤波和抽样判决后恢复出相对相对码，再经码反变换器变换成绝对码，从而恢复出发送的二进制信息。

相位比较法。其原理方框图如下图所示。用这种方法解调时不需要专门的相干载波，只需由收到的信号时延一个码元间隔T，然后与信号本身相乘。相乘起着相位比较的作用，相乘结果反映了前后码元的相位差，经低通滤波后在抽样判决，即可直接恢复出原始数字信息，故解调器中不需要码反变换器。

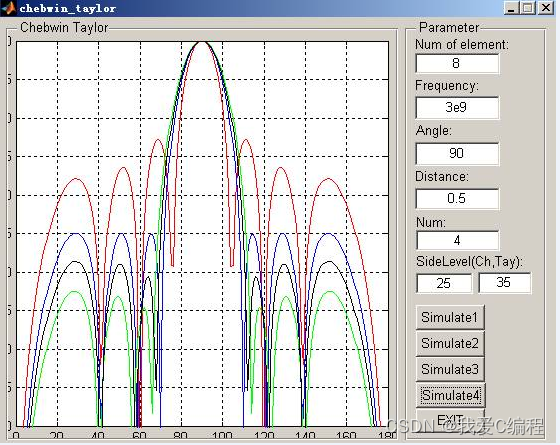
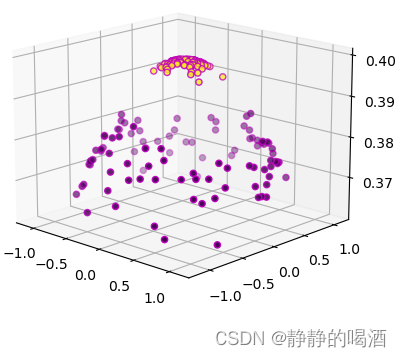
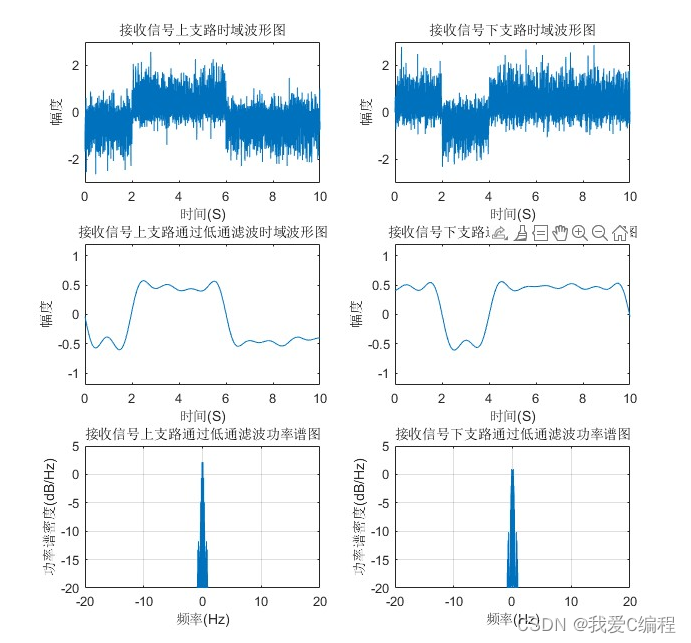
2.仿真效果预览

matlab2022a仿真结果如下：

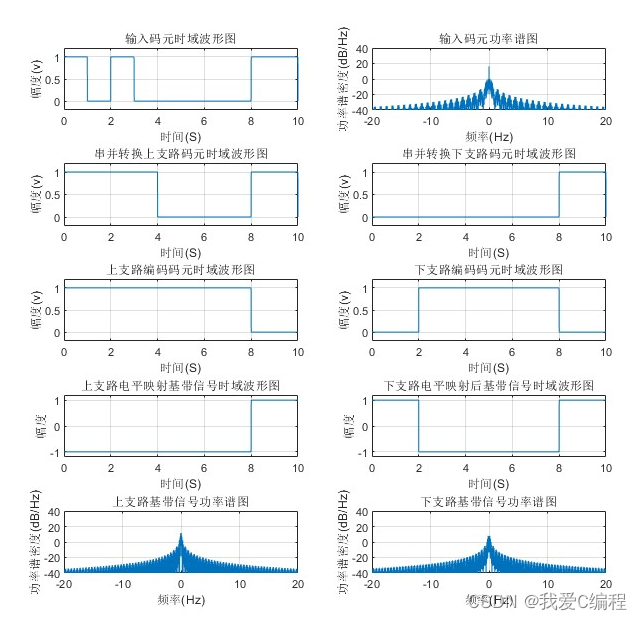
3.MATLAB部分代码预览

%pi/4-DQPSK调制解调系统的蒙特卡罗仿真
N = 10000;                            %仿真量大小
EbN0_indB = -2 : 0.5 : 12;            %仿真的信噪比点
EbN0 = 10.^(EbN0_indB/10);            %dB转换为自然值
times = 50;                           %仿真次数
err_rate = zeros(length(EbN0),times);
 
for ii = 1 : length(EbN0)
        for i = 1 : times
            r = rand(1,2*N);
            source = r>0.5;           %产生二进制信源
            b = 1 - 2*source;         %改变为反极性           
            bI = zeros(1,N);          %同相支路
            I = zeros(1,N);
            bQ = zeros(1,N);          %正交支路
            Q = zeros(1,N);
            delta = zeros(1,N);       %载波相位差
            for n = 1 : N             %串并变换
                bI(n) = b(2*n);
                bQ(n) = b(2*n-1);
                if n == 1             %差分编码  
                    I(n) = (bI(n)*bI(n) - bQ(n)*bQ(n))/sqrt(2);
                    Q(n) = (bQ(n)*bI(n) + bI(n)*bQ(n))/sqrt(2);
                else
                    I(n) = (I(n-1)*bI(n) - Q(n-1)*bQ(n))/sqrt(2);
                    Q(n) = (Q(n-1)*bI(n) + I(n-1)*bQ(n))/sqrt(2);
                end
            end
            Eb_x = cov(I);                       %信号能量
            Eb_y = cov(Q);
            sigma_x = sqrt(Eb_x/(2*EbN0(ii)));   %根据信噪比计算噪声方差
            sigma_y = sqrt(Eb_y/(2*EbN0(ii)));
            noise_x = randn(1,N)*sigma_x;        %高斯噪声产生
            noise_y = randn(1,N)*sigma_y;
            w = I + noise_x;                     %AWGN信道传输
            z = Q + noise_y;
            errornum_x = 0;              %错误数
            errornum_y = 0;
            for n = 1 : N                %差分译码
                if n == 1
                   x(n) = w(n)*w(n) + z(n)*z(n);
                   y(n) = z(n)*w(n) - w(n)*z(n);
                else
                   x(n) = w(n)*w(n-1) + z(n)*z(n-1);
                   y(n) = z(n)*w(n-1) - w(n)*z(n-1);
                end
                if x(n) <= 0                   %判决x
                    result_x(n) = -1;  
                elseif x(n) > 0
                    result_x(n) = 1;
                end
                if y(n) <= 0                   %判决y
                    result_y(n) = -1;  
                elseif y(n) > 0
                    result_y(n) = 1;
                end
                if result_x(n) ~= bI(n)        %计算x错误数
                    errornum_x = errornum_x + 1; 
                end
                if result_y(n) ~= bQ(n)        %计算y错误数
                    errornum_y = errornum_y + 1;
                end
                if errornum_x + errornum_y >= 100
                    break
                end
            end
            err_rate(ii,i) = (errornum_x + errornum_y)/(2*n);
        end
end
01_051_m