洗牌【编程题】
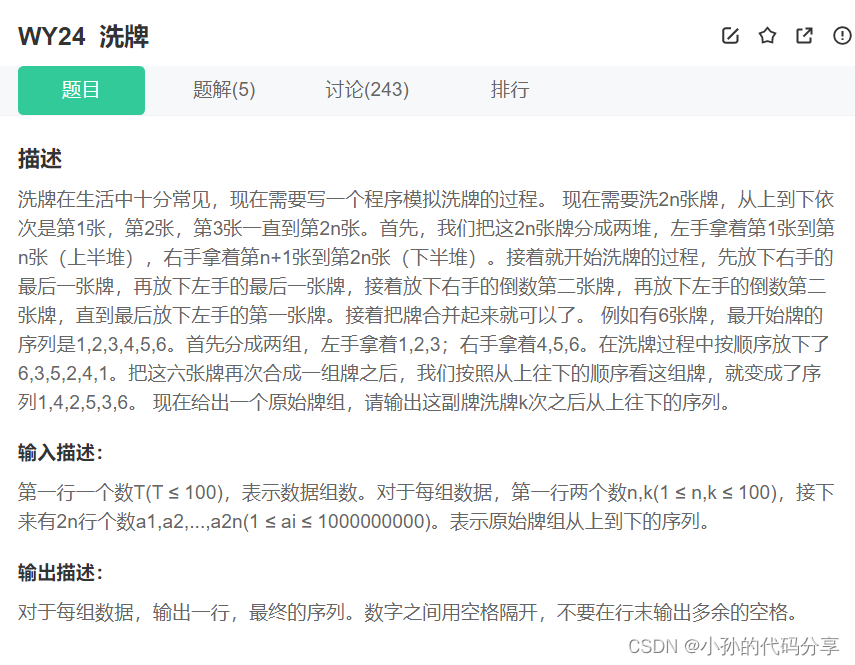
import java.util.*;
public class Main {
// 左: i --> 2*i;
// 右: i+n --> 2*i + 1;
private static void playCard(int[] cards, int n, int k ) {
for (int i = 0; i < k; i++) {
//一次洗牌的顺序
int[] newCards = new int[cards.length];
//遍历编号为0-n-1
for (int j = 0; j < n; j++) {
newCards[2 * j] = cards[j];
newCards[2 * j + 1] = cards[j + n];
}
cards = newCards;
}
//从上往下打印
printCard(cards);
}
private static void printCard(int[] cards) {
for (int i = 0; i < cards.length - 1; i++) {
System.out.print(cards[i] + " ");
}
System.out.println(cards[cards.length - 1]);
}
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
int group = scan.nextInt();
for (int i = 0; i < group; i++) {
//读入每组数据
int n = scan.nextInt();
int k = scan.nextInt();
int[] arr = new int[2 * n];
for (int j = 0; j < 2 * n; j++) {
arr[j] = scan.nextInt();
}
//洗牌
playCard(arr, n, k);
}
}
}
MP3光标位置【编程题】


import java.util.Scanner;
import java.io.*;
public class Main {
private static void mouseMove(String numStr, String orderStr) {
//歌曲数量
int n = Integer.parseInt(numStr);
//指令数组: ud
char[] order = orderStr.toCharArray();
//当前鼠标所在的位置
int mouse = 1;
//显示列表所在的起始位置
int first = 1;
//指令处理
// n <= 4
if(n <= 4) {
for(int i = 0; i < order.length; i++) {
if(mouse == 1 && order[i] == 'U') {
mouse = n;
}else if(mouse == n && order[i] == 'D') {
mouse = 1;
}else if(order[i] == 'U') {
mouse--;
}else if(order[i] == 'D') {
mouse++;
}
}
//输出
//打印当前显示列表
for(int i = 1; i < n; i++) {
System.out.print(i + " ");
}
System.out.println(n);
//打印当前歌曲
System.out.println(mouse);
} else {
// n>4
for (int i = 0; i < order.length; i++) {
if(first == 1 && mouse == 1 && order[i] == 'U') {
first = n-3;
mouse = n;
}else if (first == n-3 && mouse == n && order[i] == 'D') {
first = 1;
mouse = 1;
}else if (first != 1 && mouse == first && order[i] == 'U') {
first--;
mouse--;
//屏幕显示的不是第一页时,光标在当前屏幕最后一首歌时,按Down键显示下一首歌,这里要注意,如果是最后一页的话,按D就会到第一首歌
}else if (first != n-3 && mouse == first+3 && order[i] == 'D') {
first++;
mouse++;
//其他情况只移动光标
}else if (order[i] == 'U') {
mouse--;
}else if (order[i] == 'D') {
mouse++;
}
}
//输出
//打印当前显示列表
for(int i = first; i < first+3; i++) {
System.out.print(i + " ");
}
System.out.println(first+3);
//打印当前歌曲
System.out.println(mouse);
}
}
public static void main(String[] args) throws Exception{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
String numStr;
while((numStr = br.readLine()) != null) {
String orderStr = br.readLine();
mouseMove(numStr,orderStr);
}
}
}
年终奖【编程题】
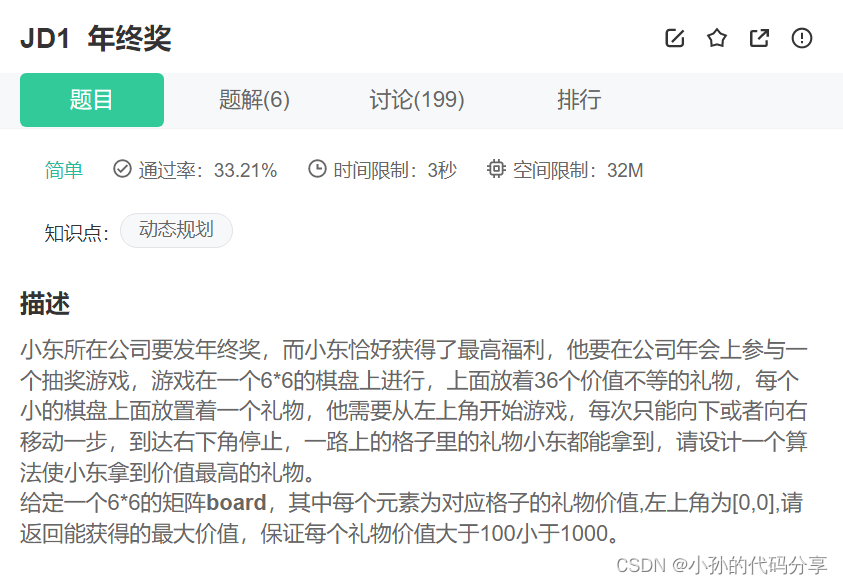
public int getMost(int[][] board) {
int row = board.length;
int col = board[0].length;
//第一行 和第一列
for (int i = 1; i < col; i++) {
board[0][i] += board[0][i-1];
}
for (int i = 1; i < row; i++) {
board[i][0] += board[i-1][0];
}
//处理剩余位置
for (int i = 1; i < row; i++) {
for (int j = 1; j < col; j++) {
board[i][j] += Math.max(board[i-1][j],board[i][j-1]);
}
}
return board[row-1][col-1];
}
迷宫问题【编程题】
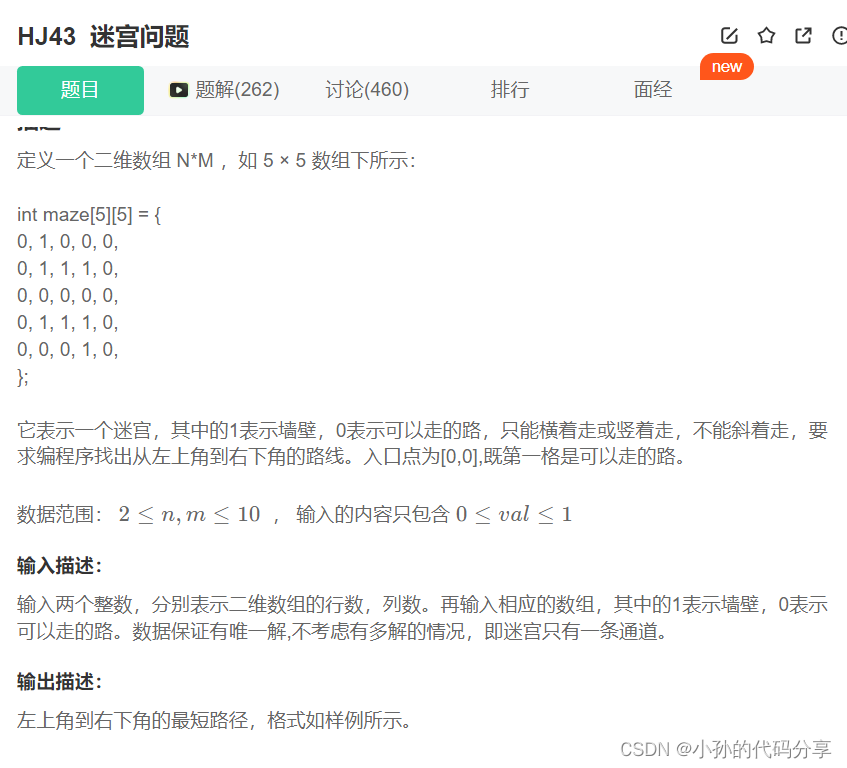
import java.util.*;
class Node {
int x;
int y;
public Node(int x, int y) {
this.x = x;
this.y = y;
}
}
public class Main {
public static void main(String[] args) {
Scanner scan = new Scanner(System.in);
int row = scan.nextInt();
int col = scan.nextInt();
//创建迷宫
int[][] mat = new int[row][col];
for (int i = 0; i < row; i++) {
for (int j = 0; j < col; j++) {
mat[i][j] = scan.nextInt();
}
}
//搜索路径
ArrayList<Node> path = new ArrayList<>();
ArrayList<Node> minPath = new ArrayList<>();
int[][] book = new int[row][col];
getMinPath(mat,row,col,0,0,book,path,minPath);
//打印路径
for(Node n : minPath) {
System.out.println("(" + n.x + ',' + n.y + ")");
}
}
//matL迷宫矩阵: row行 row列
// x,y:当前位置
// book:标记矩阵,标记当前位置是否走过
// path:保存当前路径的每一个位置
// minPath:保存最短路径
private static void getMinPath(int[][] mat, int row, int col, int x, int y, int[][] book, ArrayList<Node> path, ArrayList<Node> minPath) {
// 判断(x,y):是否越界,是否走过,是否有障碍
if(x < 0 || x >= row || y < 0 || y >= col || book[x][y] == 1 || mat[x][y] == 1) {
return;
}
//把当前位置存入路径中
path.add(new Node(x,y));
//标记当前位置
book[x][y] = 1;
//判断当前位置是否为出口
if(x == row-1 && y == col-1) {
//一条新的路径产生了
//判断是否为更短路径
if(minPath.isEmpty() || path.size() < minPath.size()) {
//更新为更短路径
minPath.clear();
for(Node n : path) {
minPath.add(n);
}
}
}
//如果不是出口,继续搜索(x,y)的上下左右四个方向
getMinPath(mat,row,col,x+1,y,book,path,minPath);//下
getMinPath(mat,row,col,x-1,y,book,path,minPath);//上
getMinPath(mat,row,col,x,y+1,book,path,minPath);//右
getMinPath(mat,row,col,x,y-1,book,path,minPath);//左
//把当前位置从路径中删除,寻找新的路径
path.remove(path.size()-1);
book[x][y] = 0;//回退了,表示没有走过,改为0
}
}
1. 堆是从任意结点出发到根路径上所经过的结点序列按其关键字有序【大根堆/小根堆】
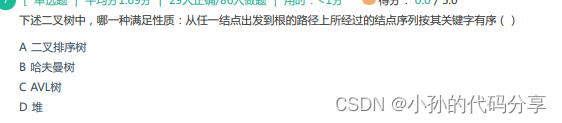
A:二叉排序树(BST):
- 如果左子树不空,那么左子树上所有结点的值均小于根结点。
- 如果右子树不空,那么右子树上所有结点的1值均大于根结点。
B:哈夫曼树:
- 带权值的树
C:AVL树:【平衡二叉查找树】
- 树中任意结点的两个子树高度最大差为1,那么这棵树就是高度平衡树
D:堆:
- 分为大根堆-小根堆
- 如果是大根堆(小根堆),堆中所有结点都满足:根结点大于(小于)左右孩子结点。
由四个选项的特点可以看出,二叉排序树只在根结点处有序,其余子节点无序,所以pass A选项;哈夫曼树是无序的;AVL树也是无序的;只有D选项属于根结点有序,子节点有序,所以选择D。
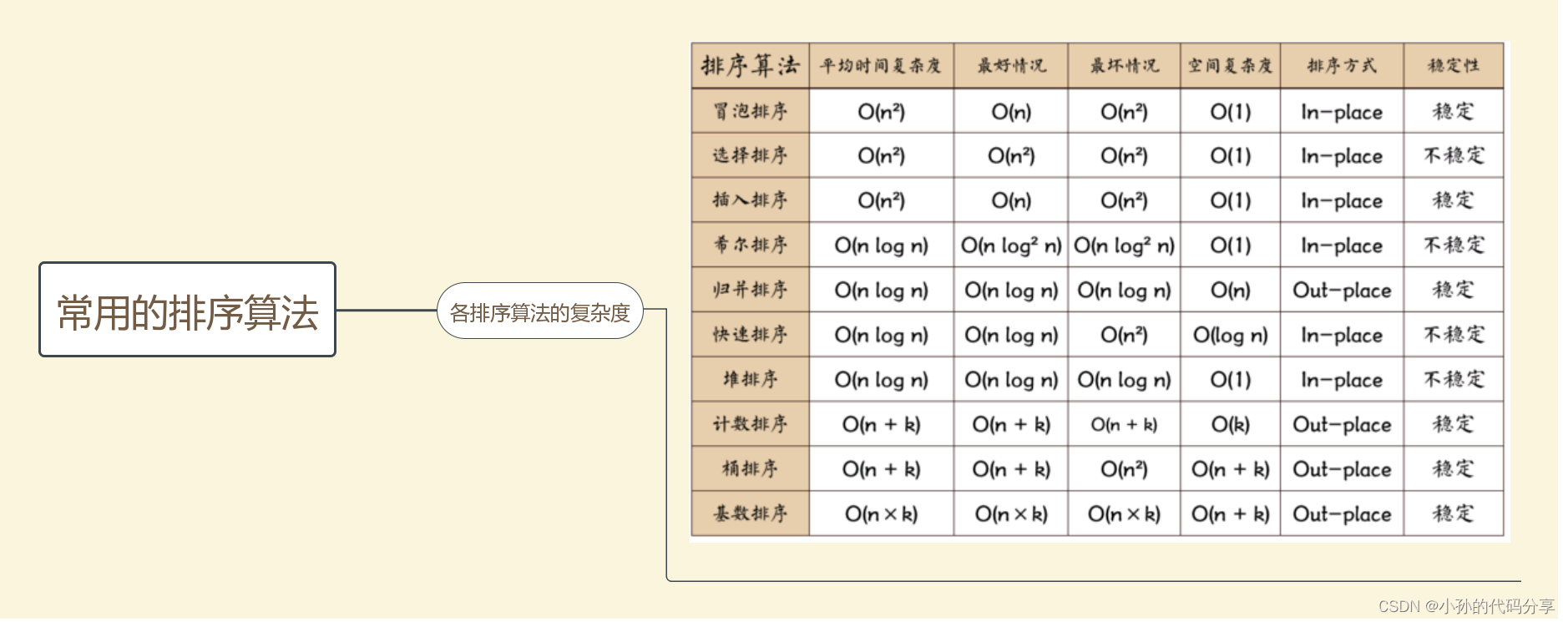
2.将整数数组(7-6-3-5-4-1-2)按照堆排序的方式原地进行升序排列,请问在第一轮排序结束之后,数组的顺序是(C)

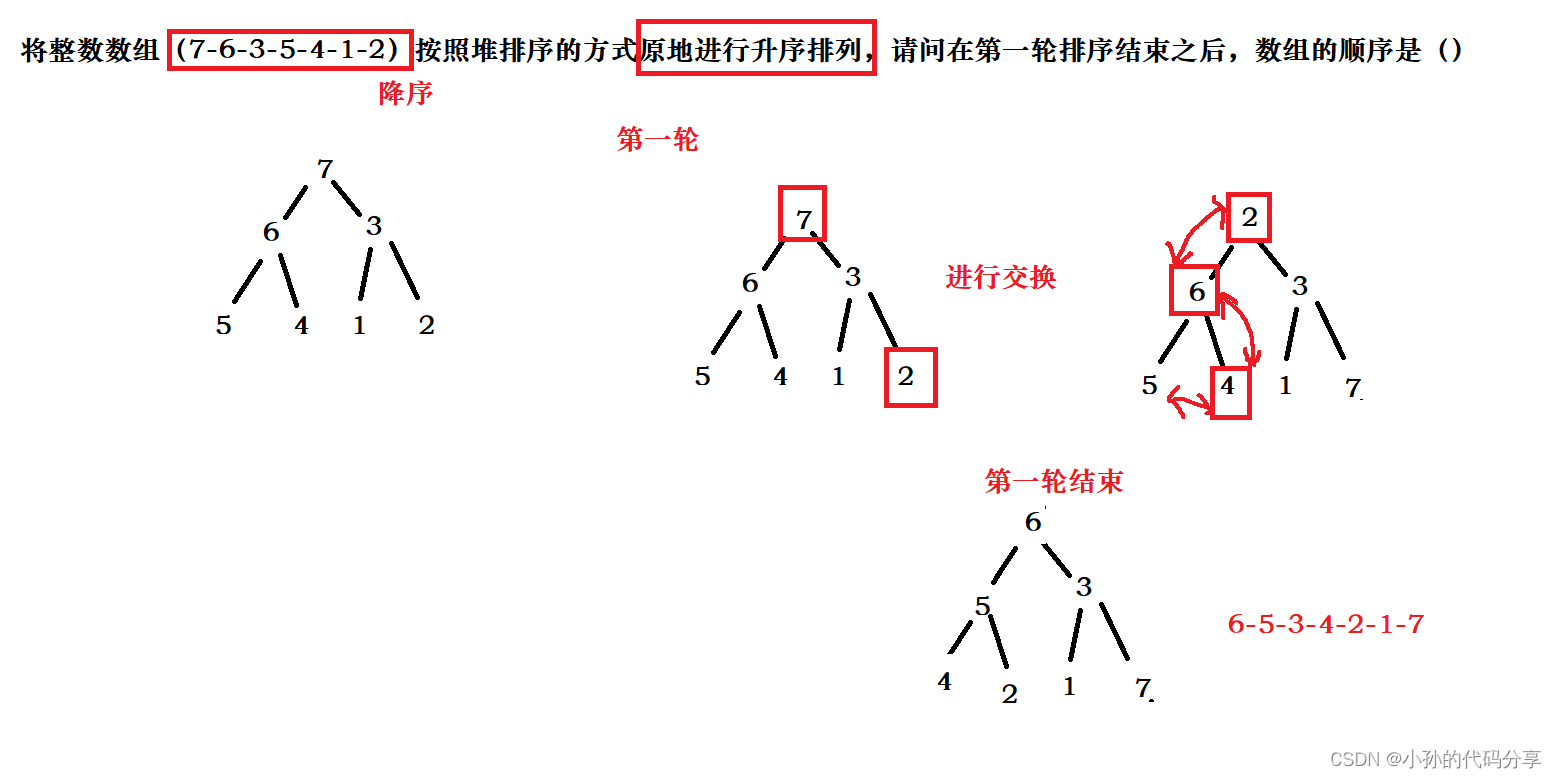
3.排序方法的最坏时间复杂度
堆排序最坏情况时间下的时间复杂度为 O(nlog2n) ;
希尔排序最坏情况时间下的时间复杂度为 O(n1.5) ;
快速排序、冒泡排序最坏情况时间下的时间复杂度为O(n2) 。
4.HASH 函数冲突处理方式
A 开放定址法
B 链地址法
C 插入排序法
5.二叉排序树特点
(B)二叉排序树可以得到一个从小到大的有序序列。
A 先序遍历
B 中序遍历
C 后序遍
D 层次遍历
-
二叉排序树(BST):
-
如果左子树不空,那么左子树上所有结点的值均小于根结点。
-
如果右子树不空,那么右子树上所有结点的1值均大于根结点。
可以看出二叉排序树属于 左小右大,所以中序遍历就可以完成从小到大的有序序列
6.快排确定第几趟排序结果,要看有几个数满足左边大右边小的条件


7.堆排序平均执行的时间复杂度和需要附加的存储空间复杂度分别是(B)
A O(N2)和O(1)
B O(Nlog2N)和O(1)
C O(Nlog2N)和O(N)
D O(N2)和O(N)