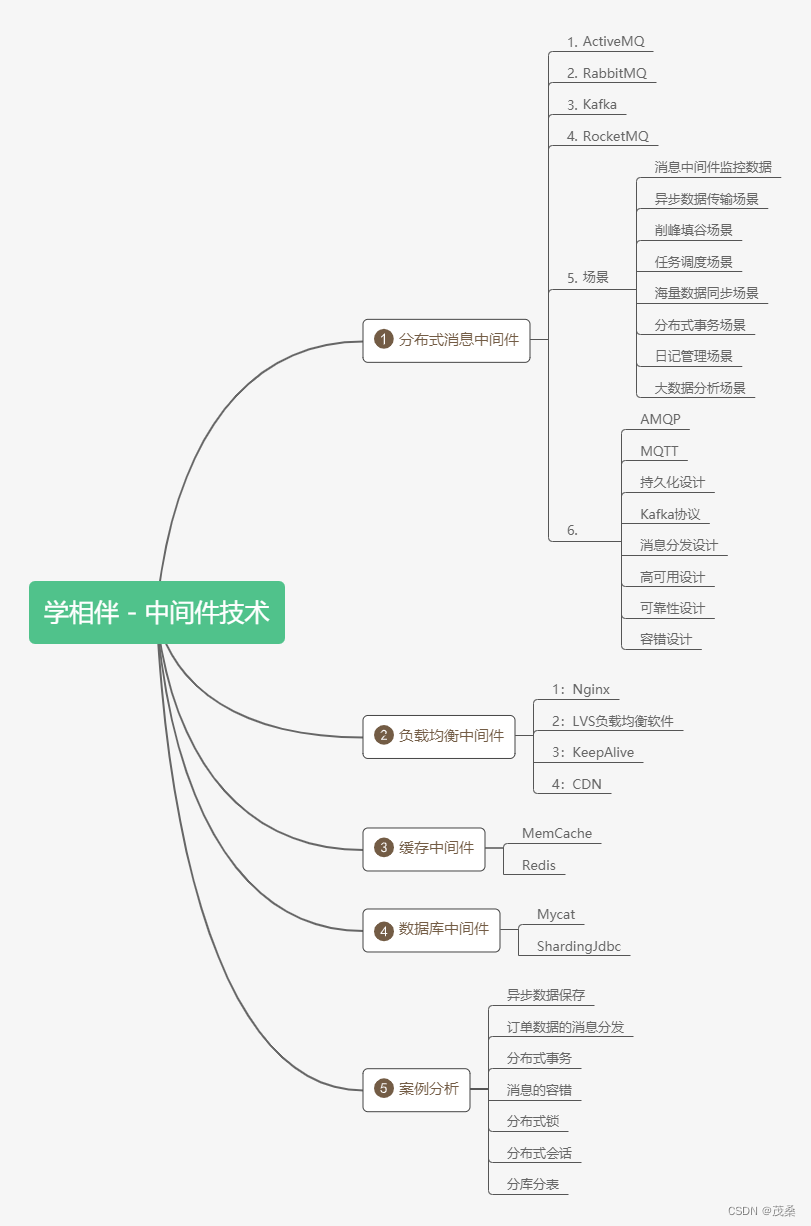
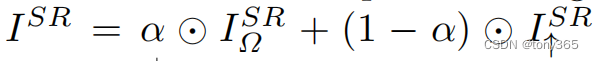文章一：Rethinking the Backdoor Attacks’ Triggers: A Frequency Perspective

文章贡献：

• 在频域上对现有的 backdoor trigger 进行分析，发现常见 trigger 存在 high-frequency artifacts 的问题。
• 对这些 artifacts 进行了详细的分析
• 展示了在频域空间中检测 trigger 的有效性
• 提出了一种方法，生成不具有 high-frequency artifacts 的 trigger ，并且对其的可检测性进行了分析

Frequency Artifacts

作者通过 type-II 2D-DCT 变换，将图片从空域转换到频域。

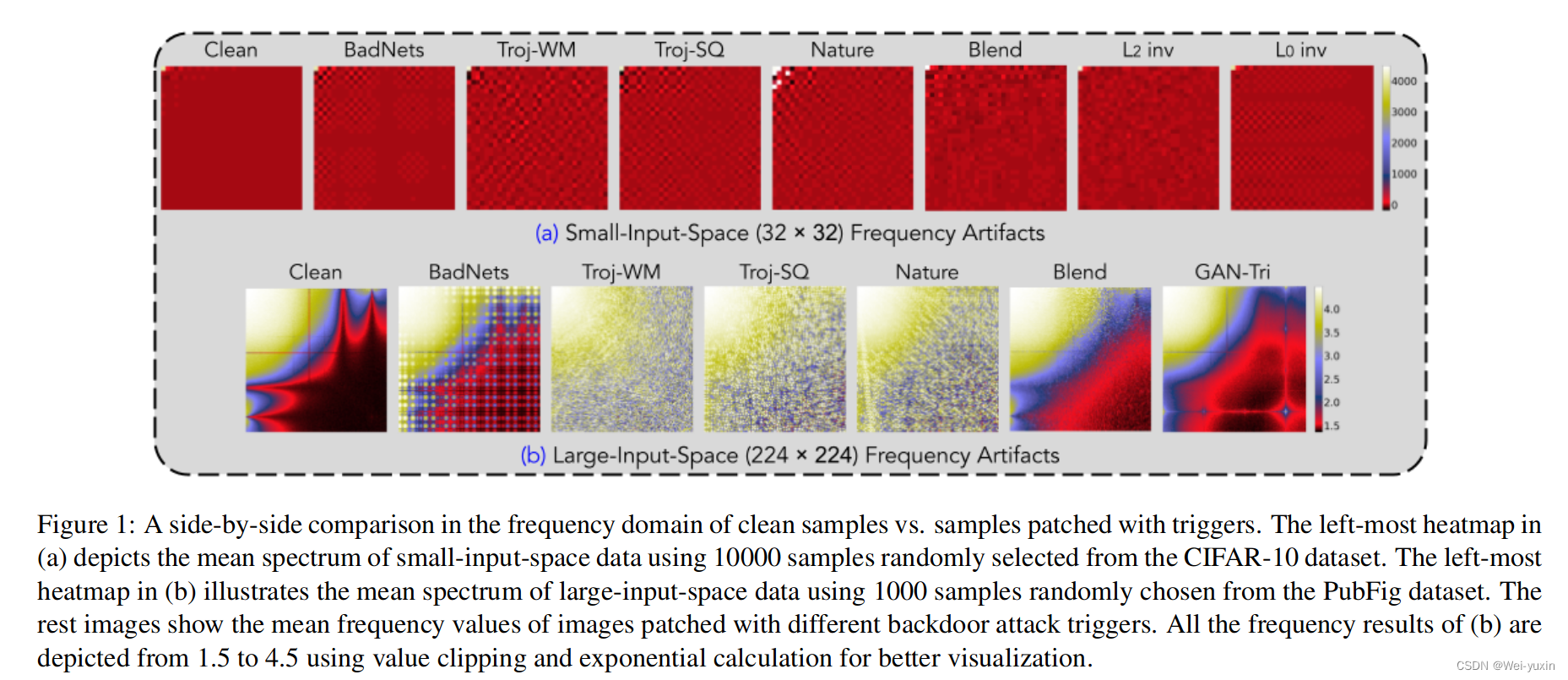
Analyzing Causes of High-Frequency Artifacts

• Local Patching

  By the linearity of DCT, adding a trigger to an image is equivalent to adding the trigger’s frequency spectrum to the image’s spectrum.

• Large-Size or Global Patching

  相邻像素之间相关性降低，触发器携带的高频信息

• GAN-Generated Backdoor Data

  GAN中使用的上采样导致 high-frequency artifacts （引用文章 ）

Frequency-Based Backdoor Data Detection

关于使用频域信息进行防御，未阅读。

Creating Smooth Triggers

• 问题定义：

  ${\min }_{\delta }{\Sigma }_{i}L\left(x_i+\delta ,y_{\text{tar }};{\theta }_p\right)+\lambda \Omega (\delta ;g)$,
  s.t. $\underset{i=1,\dots ,N}{\underbrace{x_i+\delta }}\in [0,1{]}^n$,

  We adopt $\Omega (\cdot ;g)$ from SmoothFool

  ${\theta }_p={\mathrm{argmin}}_{\theta }\left({\Sigma }_{i}L\left(x_i,y_i;\theta \right)+{\Sigma }_{j}L\left(x_j+\delta ,y_{tar};\theta \right)\right)$

  关于 trigger 的生成，文中采用了：每一次迭代后，将扰动通过低通滤波器再更新触发器。 (pdf)

• 因此生成 trigger 的公式变为：

  ${\min }_r{\Sigma }_{i}L\left(x_i^{poi},y_{tar};{\theta }_{poi}\right)$,
  s.t. $r=\delta \ast g$,
  $\underset{i=1,\dots ,N}{\underbrace{x_i^{poi}=M\left(x_i+\lambda r\right)}}$,

  • 其中 $r$ 为扰动与低通滤波器卷积后的结果。
  • $M$ 代表标准化的过程，让 posion image 限制到 [0, 1]
  • 标准化可以更好地保持像素间的比例

• 生成 trigger 的可视化

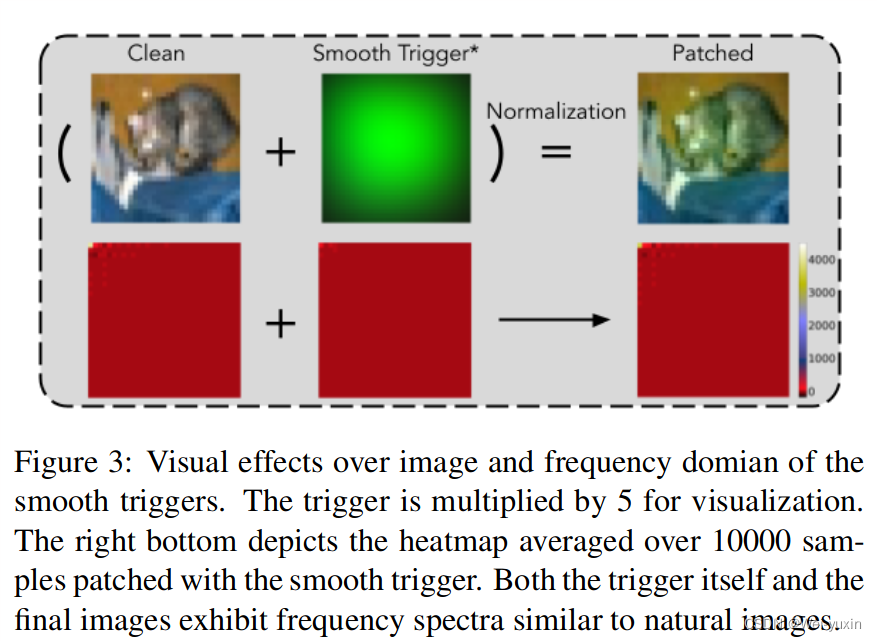
由图所示，High-Frequency Artifacts 减少了。

但是生成的 trigger 有点发绿，看起来效果一般般​

文章二：Backdoor Attack through Frequency Domain

• Backdoor Attack through Frequency Domain

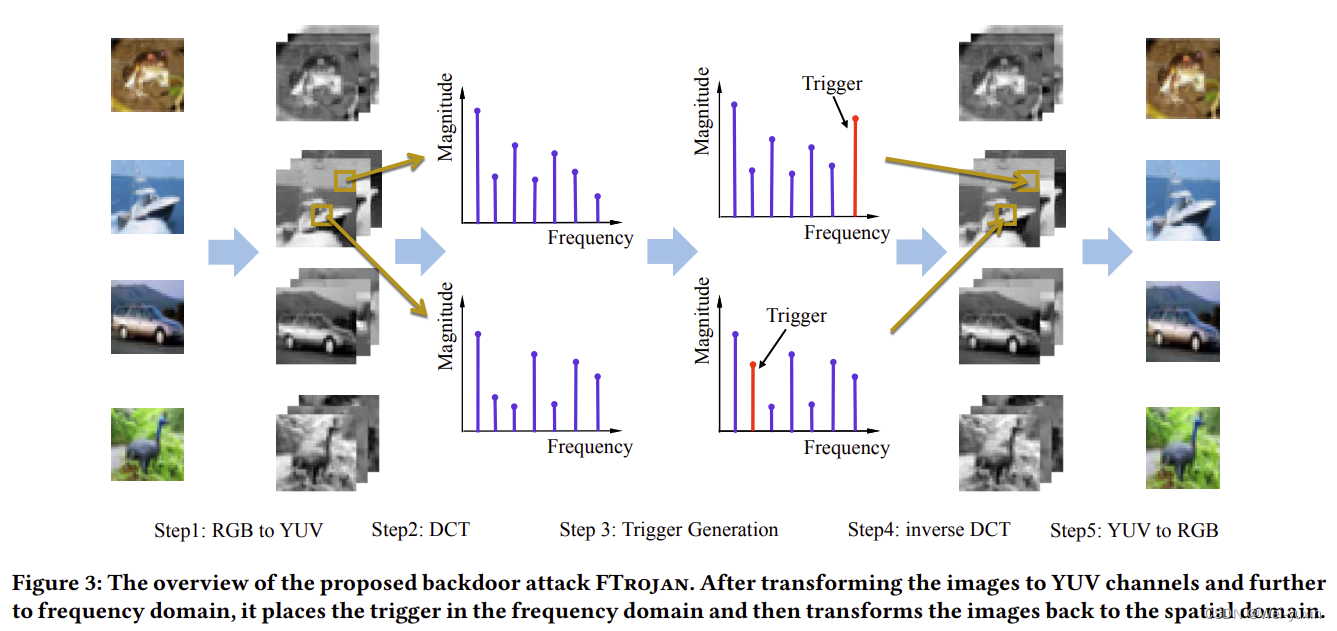
五个步骤：

1. color channel transform from RGB to YUV
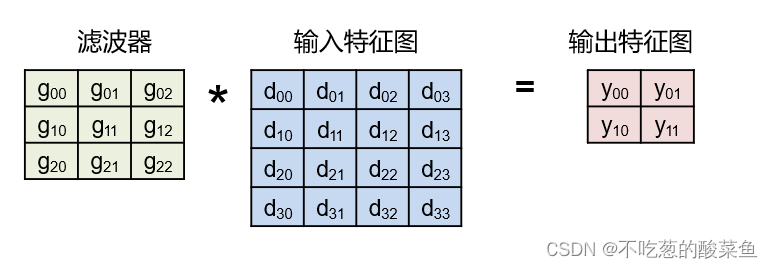
2. discrete cosine transform from spatial domain to frequency domain
3. trigger generation in the frequency domain
4. inverse discrete cosine transform from frequency domain to spatial domain
5. color channel transform from YUV to RGB

FFT：

幅度谱（amplitude spectrum）与相位谱（phase spectrum）