文章目录
- 1 归并排序简介
- 2 思路简介及图解
- 3 代码实现
- 写在最后
1 归并排序简介
归并排序是建立在归并操作上的一种有效,稳定的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
归并排序是稳定排序,它也是一种十分高效的排序,能利用完全二叉树特性的排序一般性能都不会太差。java中Arrays.sort()采用了一种名为TimSort的排序算法,就是归并排序的优化版本。
2 思路简介及图解
以序列8、4、5、7、1、3、6、2为例
分而治之
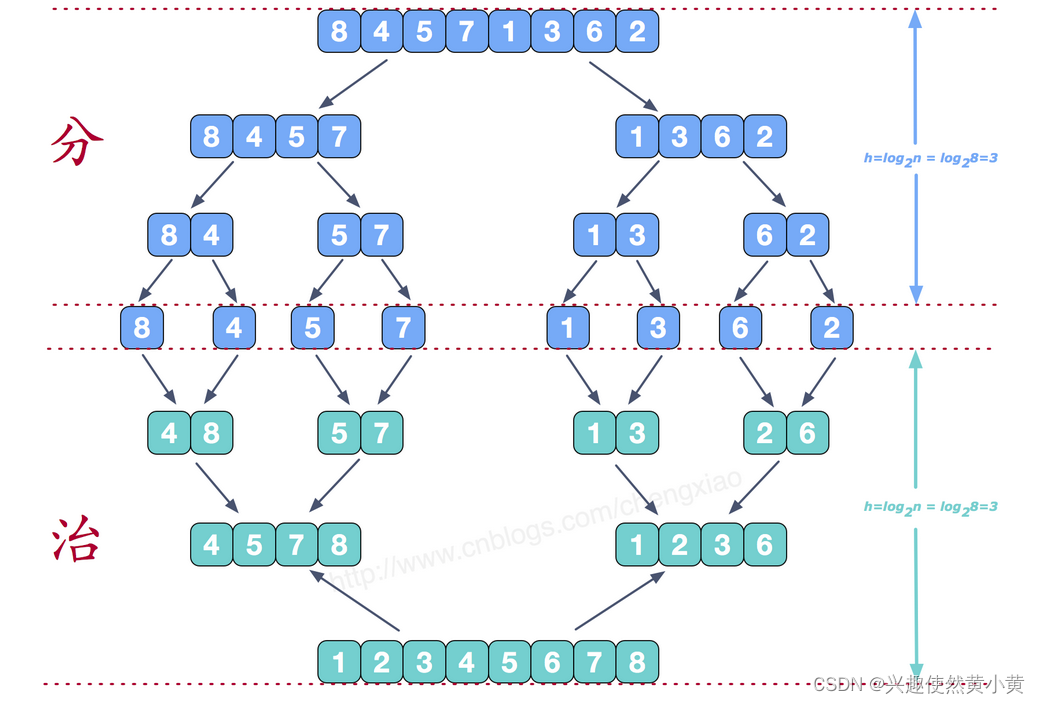
可以看到这种结构很像一棵完全二叉树。分阶段可以理解为就是递归拆分子序列的过程,递归深度为log2n。
合并相邻有序子序列
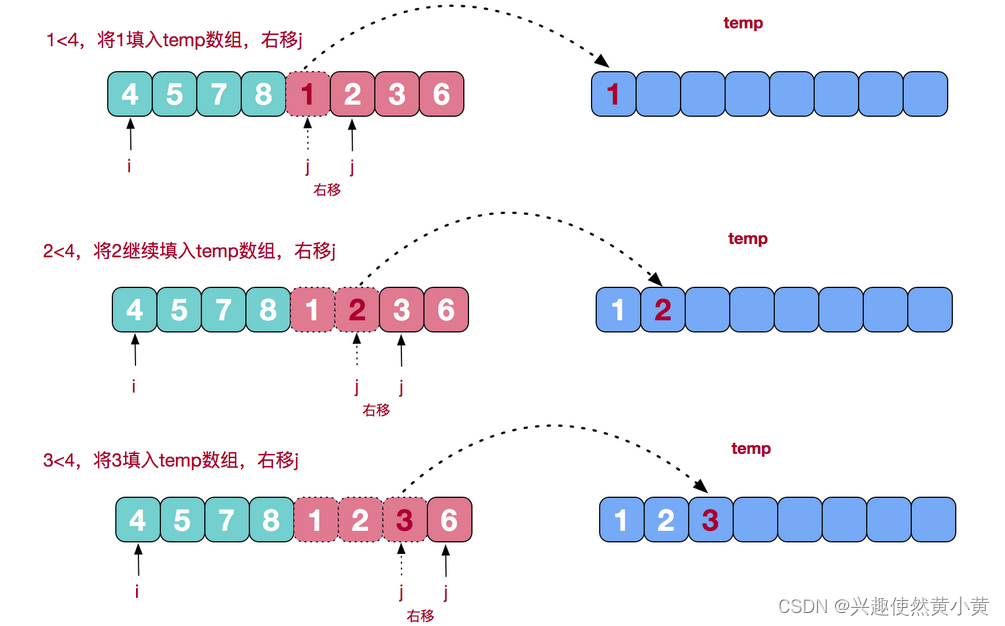
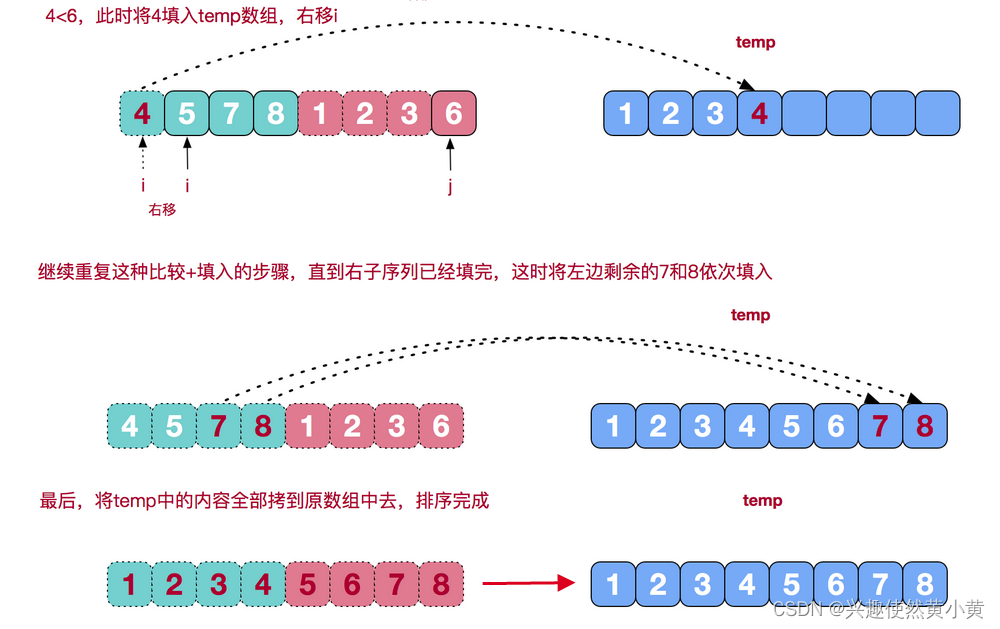
从上文的图中可看出,每次合并操作的平均时间复杂度为O(n),而完全二叉树的深度为|log2n|。总的平均时间复杂度为O(nlogn)。而且,归并排序的最好,最坏,平均时间复杂度均为O(nlogn)。
3 代码实现
import java.util.Arrays;
/**
* @author 兴趣使然黄小黄
* @version 1.0
* 递归实现归并排序
*/
@SuppressWarnings({"all"})
public class MergetSort {
static int count = 0;
public static void main(String[] args) {
int[] arr = {8, 4, 5, 7, 1, 3, 6, 2};
int[] temp = new int[arr.length];
mergeSort(arr, 0, arr.length - 1, temp);
System.out.println("归并排序后: arr[] = " + Arrays.toString(arr));
}
//归并排序
public static void mergeSort(int[] arr, int left, int right, int[] temp){
if (left < right){
int mid = left - (left - right) / 2;
//向左递归分解
mergeSort(arr, left, mid, temp);
//向右递归分解
mergeSort(arr, mid + 1, right, temp);
//排序 合并
merge(arr, left, mid, right, temp);
}
}
/**
* 合并的方法
* @param arr 排序的原始数组
* @param left 左边有序序列的初始索引
* @param mid 中间索引
* @param right 右边索引
* @param temp 中转数组
*/
public static void merge(int[] arr, int left, int mid, int right, int[] temp){
int i = left; //初始化i,左边有序序列的初始索引
int j = mid + 1; //初始化j,右边有序序列的初始索引
int t = 0; //指向temp数组的当前索引
//先把左右两边有序数据按照规则填充到temp数组,直到左右两边有一边处理完毕
while (i <= mid && j <= right){
if (arr[i] <= arr[j]){
temp[t] = arr[i];
t++;
i++;
}else {
temp[t] = arr[j];
t++;
j++;
}
}
//把剩余的一方依次填充到temp数组
while (i <= mid){ //左边序列还有剩余的元素
temp[t++] = arr[i++];
}
while (j <= right){ //右边序列还有剩余的元素
temp[t++] = arr[j++];
}
//将temp数组的元素拷贝到arr
//拷贝每次小序列
t = 0;
int tempLeft = left;
while (tempLeft <= right){
arr[tempLeft++] = temp[t++];
}
// System.out.println("=====" + Arrays.toString(arr));
// System.out.println(Arrays.toString(temp));
count++;
System.out.println("第" + count + "次合并: arr[] = " + Arrays.toString(arr));
// System.out.println("第" + count + "次合并: temp[] = " + Arrays.toString(temp));
}
}
实现结果如下:
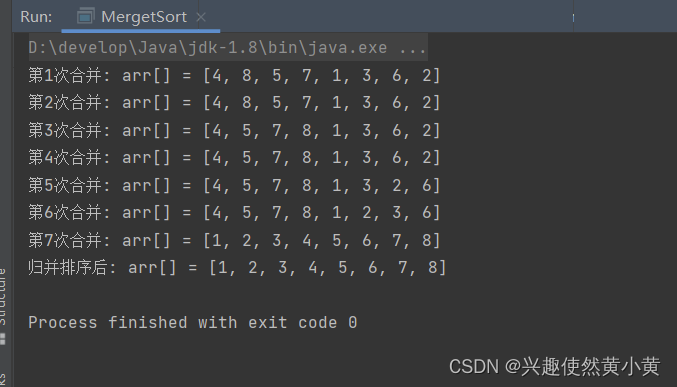
这样看还是不好看出归并排序的过程,我们尝试把测试用例修改成{8, 7, 6, 5, 4, 3, 2, 1}:
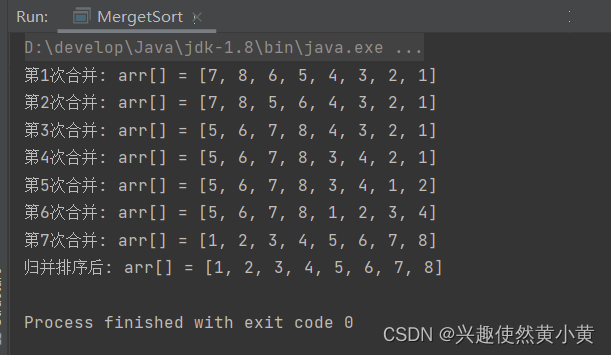 {8, 7, 6, 5, 4, 3, 2, 1}被拆分成了{8, 7}{6, 5}{4, 3}{2, 1}:
{8, 7, 6, 5, 4, 3, 2, 1}被拆分成了{8, 7}{6, 5}{4, 3}{2, 1}:
- 第一次合并:{7, 8}有序
- 第二次合并:{5, 6}有序
- 第三次合并: {5, 6, 7, 8}有序
- 第四次合并:{3, 4}有序
- 第五次合并:{1, 2}有序
- 第六次合并: {1, 2, 3, 4}有序
- 第七次合并:{1,2,3,4,5,6,7,8}有序
写在最后
本文被 Java数据结构 收录点击订阅专栏 , 持续更新中。本文图片来自网络,仅供学习使用。
创作不易,如果你有任何问题,欢迎私信,感谢您的支持!