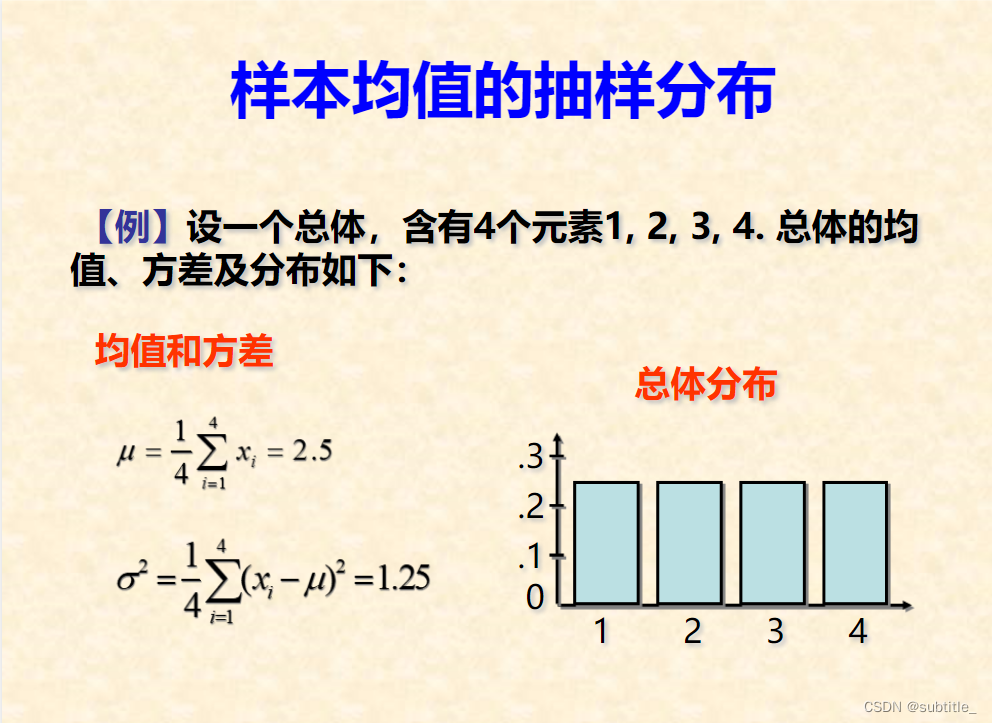
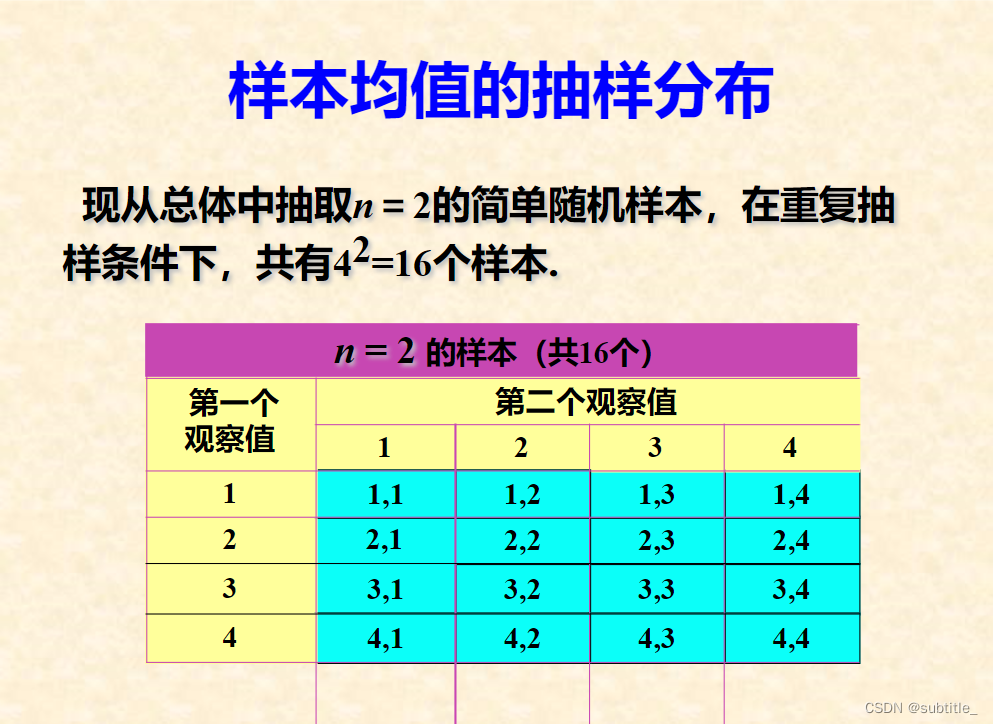
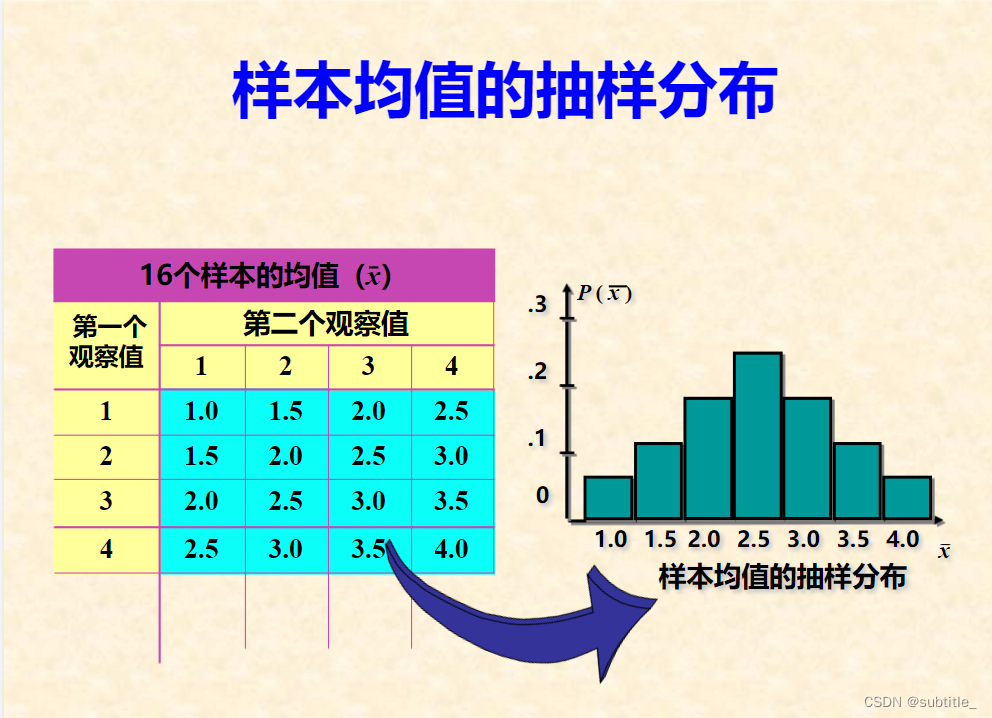
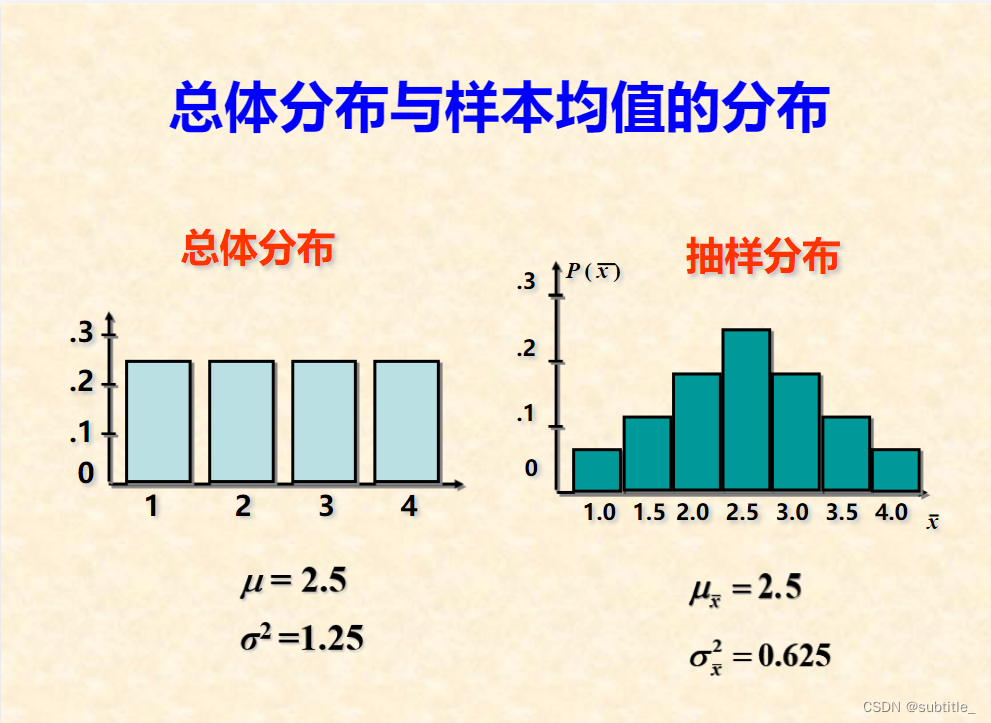
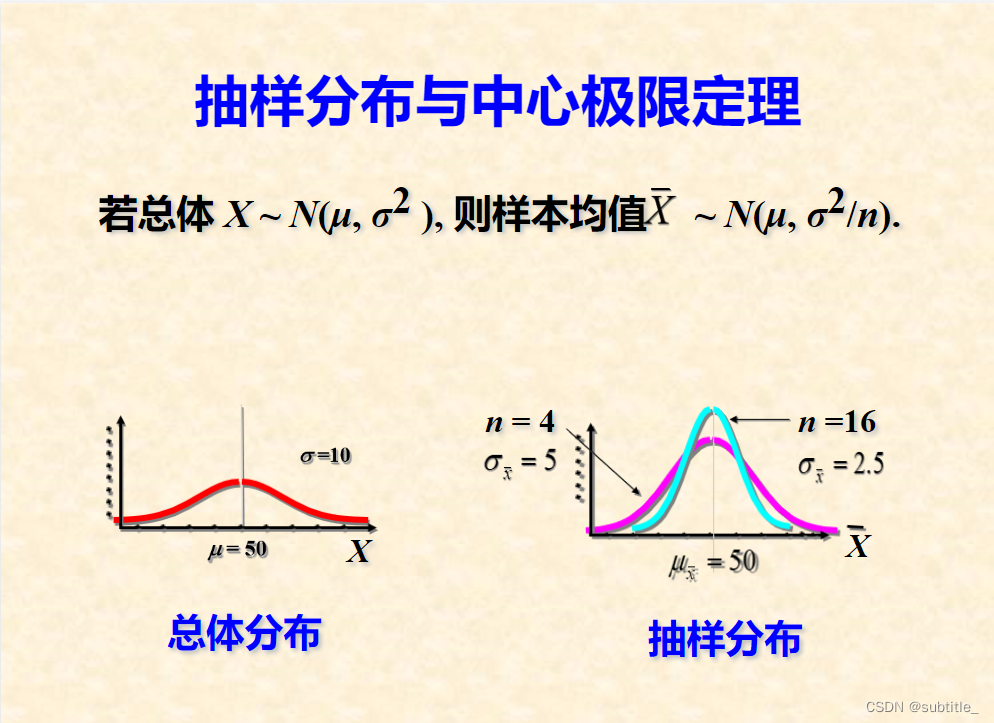
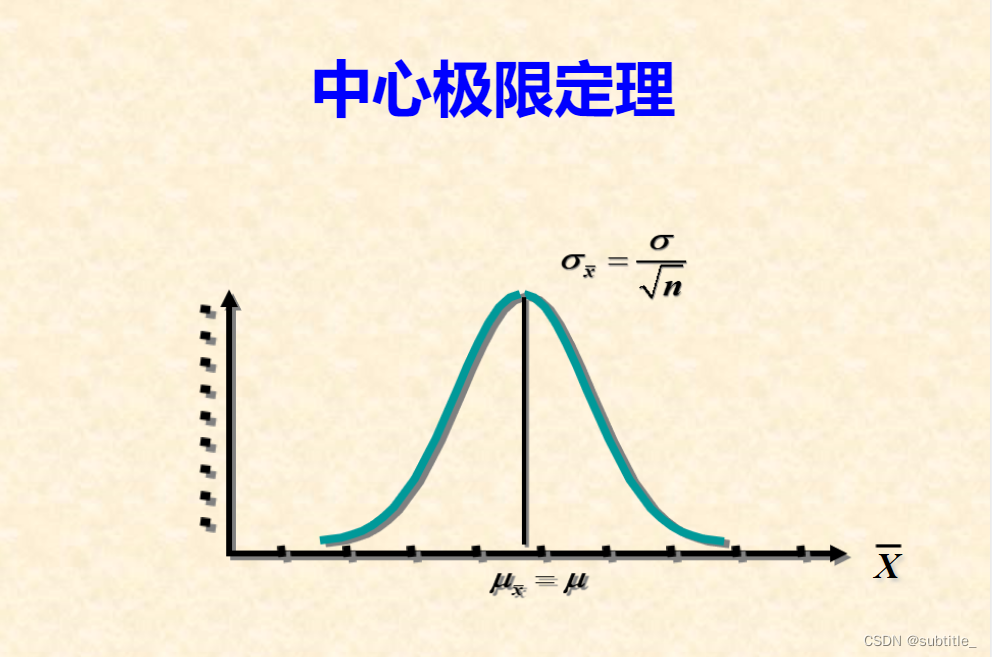
数理统计笔记2:总体均值的抽样分布
news2026/2/10 6:45:38
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/27620.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
sqli-labs/Less-50
这一关仍然是以sort作为注入点的
首先我们输入rand() 判断是数字型还是字符型
多次尝试 发生变化 说明属于数字型
接着试试报错注入 输入以下语句
sortupdatexml(1,if(11,concat(0x7e,database(),0x7e),1),1)--
存在回显 说明可以使用报错注入哦 这一关要训练的是堆叠注入…
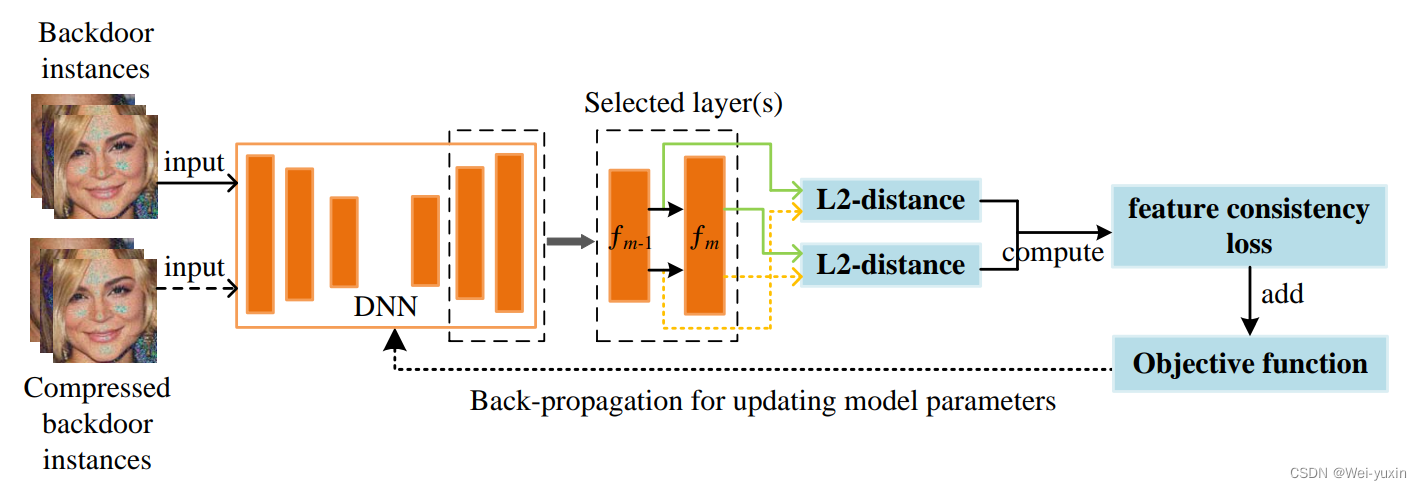
Compression-Resistant Backdoor Attack against Deep Neural Networks 论文笔记
论文名称Compression-Resistant Backdoor Attack against Deep Neural Networks作者Mingfu Xue(南京航空航天大学)会议/出版社未发表pdf📄在线pdf代码无概要本文提出了一种对图像压缩(JPEG,JPEG2000,WEBP&a…
Linux进阶-文件
Linux内核:屏蔽硬件区别,把所有的硬件设备抽象成文件,提供统一的接口给用户使用。
目录
虚拟文件系统:抽象层,对文件的访问实际上是对抽象层的访问。
普通文件系统:ext4、fat32、ubifs
特殊文件系统
文…
NestJS学习:搭建项目、依赖注入、常用命令、RESTful 风格设计
介绍
Nest (NestJS) 是一个用于构建高效、可扩展的 Node.js 服务器端应用程序的开发框架。它利用 JavaScript 的渐进增强的能力,使用并完全支持 TypeScript (仍然允许开发者使用纯 JavaScript 进行开发),并结合了 OOP ࿰…
现代密码学导论-4-完美保密及其三个等价定义
目录
完美保密 Perfectly Secret Encryption
2.1 完美保密的定义
DEFINITION 2.3 完美保密加密方案的定义
LEMMA 2.5 完美保密方案的等价定义(一)
证明引理2.5与定义2.3等价
完美不可区分性
不可区分实验 The adversarial indistinguishability experiment
DEFINITION …
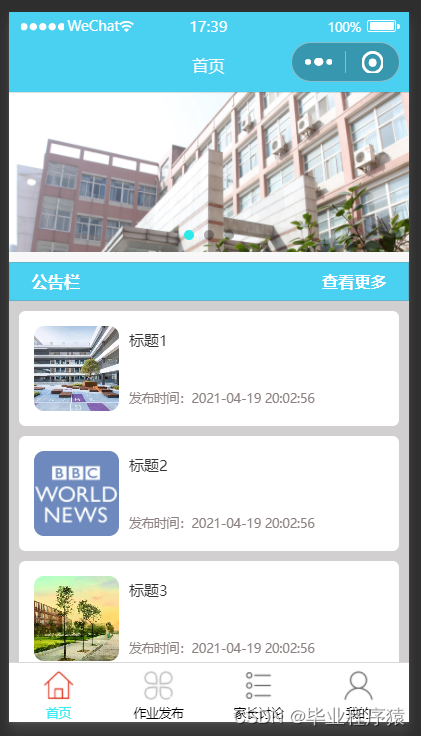
基于微信小程序的家校通系统-JAVA【数据库设计、源码、开题报告】
第一章 绪 论
1.1选题背景
随着网络时代的到来,互联网的优势和普及时刻影响并改变着人们的生活方式。在信息技术迅速发展的今天,计算机技术已经遍及全球,使社会发生了巨大的变革。
为了不受时间和地点的限制,智能手机用户可以通…
MySQL学习笔记-----Navicat设置建表
1.数据库字段设置 id 主要设置有bigint 和int两种 长度一般都是20 字符 主要设置 varchar 长度 我一般设置 255 时间 主要是设置为timestamp 混合日期和时间值,时间戳 ,建议在java端的DTO或者request设置时间格式 判断状态 比如mybatis-pl…
宋祖德六评岳云鹏,大饼脸、文化低、总有一句能戳中你的内心
都知道娱乐圈有一个纪委书记,那就是万达的公子王思聪,其实在郭德纲的北京德云社,也有一位义务纪委书记。著名导演宋祖德,就是德云社的纪委书记,这些年他把所有的重心,都放在了约束德云社上面。
俗话说&…
Mysql优化-经验分享
目录什么是索引索引类型主键索引唯一索引组合索引前缀索引全文索引空间索引索引的数据结构HASH表二叉树平衡二叉树红黑树B树B树索引的存储引擎MyISAMInnoDB索引优化方向分层SQL优化表设计三范式索引合理使用服务器优化内存升级碎片优化工具的使用explainshow processlistshow p…
书法比赛评分系统-JAVA【数据库设计、源码、开题报告】
1 引言
1.1 选题背景及意义
书法艺术,是中国的国粹;是经过数千年历史积淀和先哲们上下求索而形成的灿烂的文化瑰宝;是囊括了人与天地之间的大学问;是中华民族智慧的结晶;是最具中国特色的文化艺术门类。它不仅在中国,而且在世界上也享有极高的荣誉&…
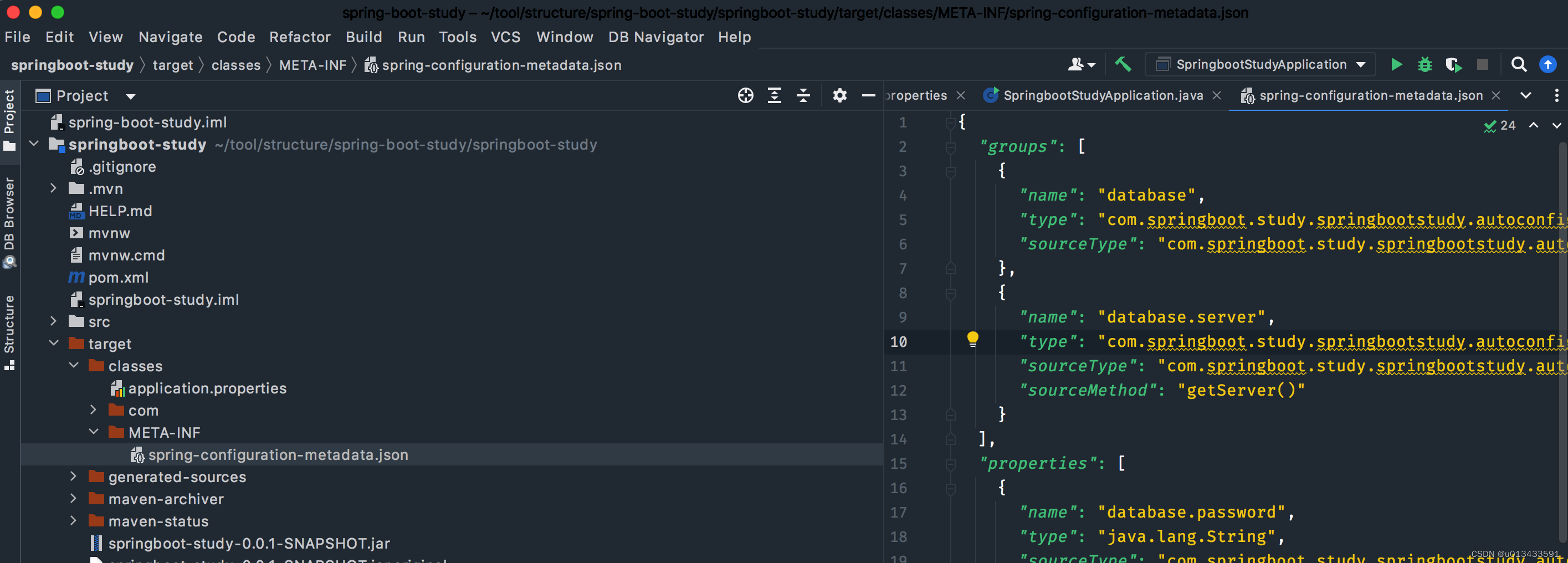
Spring Boot 自定义配置元数据
Spring Boot 自定义配置元数据
概述
开发Spring Boot应用程序时, 可以把 application.properties文件中的配置属性直接转换为 Java Bean对象。这也是Spring Boot 约定大于配置的理念的体现,通过框架内置的各种属性按照不同的需求进行排列组合,满足特定…
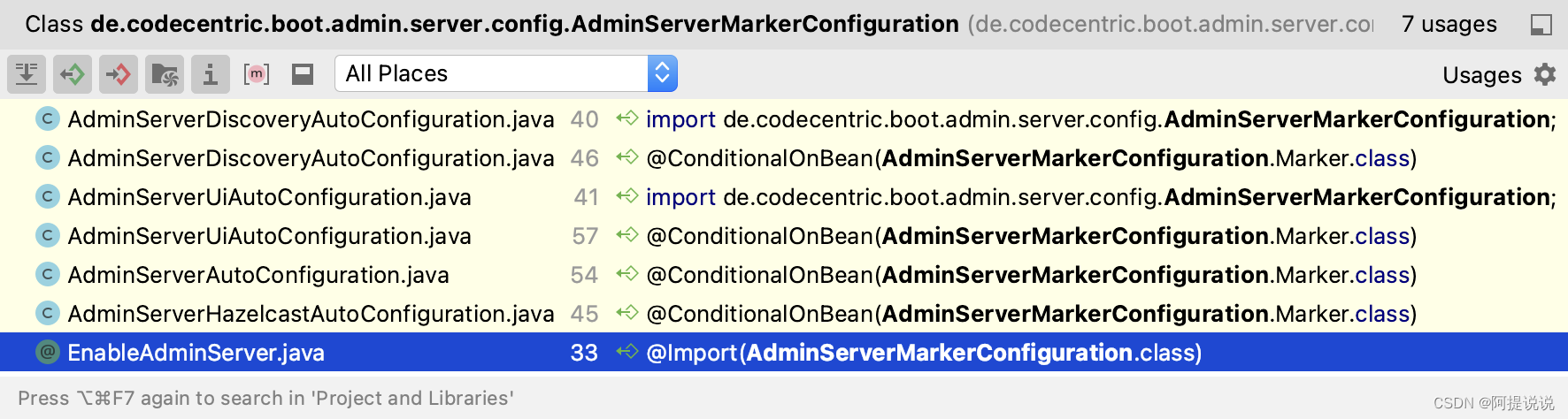
Spring Boot Admin2 @EnableAdminServer的加载
其他相关文章: 1、Spring Boot Admin 参考指南 2、SpringBoot Admin服务离线、不显示健康信息的问题 首先根据官网的“快速开始”,快速搭建一个Spring Boot Admin Server项目 1、添加Spring Boot Admin启动器到依赖 pom.xml
<dependency><grou…
低代码会使初级码农失业吗?
低代码的目的是提升效率,不是压榨生存空间。低代码不代表低技术,所以低代码并不会导致初级码农失业,实际上不仅不会导致失业,还帮助更多人走上了“开发者”岗位。
何为低代码?
所谓“低代码”(Low-Code&a…
day29 SQL注入增删改查盲注延时布尔报错
前言
#知识点:
1、明确查询方式注入Payload
2、明确查询方式注入产生功能
3、明确SQL盲注延时&布尔&报错 #详细点:
盲注就是在注入过程中,获取的数据不能回显至前端页面。
此时,我们需要利用一些方法进行判断或者尝…
基于JAVA的房屋租赁系统平台【数据库设计、源码、开题报告】
数据库脚本下载地址: https://download.csdn.net/download/itrjxxs_com/86427640
租户在租房过程中如何才能保护自己的合法权益?
出租方在租房过程中又如何证明房屋的所属关系?种种租赁相关话题,成了当下关注的民生热点,为了切实解决人民群…
BUUCTF Reverse/[GXYCTF2019]simple CPP
BUUCTF Reverse/[GXYCTF2019]simple CPP 先看文件信息,是个64位的程序,且没有加壳 IDA64位打开 int __cdecl main(int argc, const char **argv, const char **envp)
{bool v3; // si__int64 v4; // rax__int64 v5; // r8__int64 v6; // r8unsigned __in…
【ESP32_8266_MQTT篇】
文章目录MQTT介绍1 MQTT历史2 MQTT版本MQTT介绍 MQTT是一个客户端服务端架构的发布/订阅模式的消息传输协议。它的设计思想是轻巧、开放、简单、规范,易于实现。这些特点使得它对很多场景来说都是很好的选择,特别是对于受限的环境如机器与机器的通信&…
Java面向对象的特点之:继承
对于继承,当大家看到这个词语的时候,在现实生活中,想必也会自然而然的想到了:继承家产??那么,在Java的面向对象的时候,也存在这样的思想!!
下面笔者来带领大…



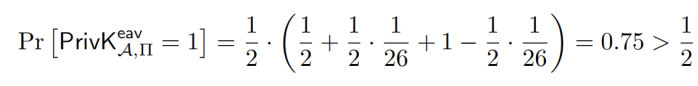





![BUUCTF Reverse/[GXYCTF2019]simple CPP](https://img-blog.csdnimg.cn/eb07f46c30c3402eb0e34012b251689c.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L29va2FtaTY0OTc=,size_16,color_FFFFFF,t_70#pic_center)

