目录
完美保密 Perfectly Secret Encryption
2.1 完美保密的定义
DEFINITION 2.3 完美保密加密方案的定义
LEMMA 2.5 完美保密方案的等价定义(一)
证明引理2.5与定义2.3等价
完美不可区分性
不可区分实验 The adversarial indistinguishability experiment
DEFINITION 2.6 完美不可区分方案的定义
LEMMA 2.7 完美保密方案的等价定义(二)
证明引理2.7与定义2.3等价
Example 2.8 证明维吉尼亚密码体制不满足完美不可区分
-
完美保密 Perfectly Secret Encryption
在上一章中,我们介绍了一些历史上的加密方案,并表明它们很容易被破解。在本章中,我们研究了另一个极端,并研究了即使在具有无限计算能力的对手面前也可证明安全的加密方案。这种计划被称为完美保密。我们严格定义了这一概念,并探索了实现完美保密的条件。在某种意义上,本章中的材料更多地属于“古典”密码学的世界,而不是“现代”密码学的。除了这里介绍的所有材料都是在20世纪70年代中期和80年代发生的密码学革命之前开发的这一事实之外,我们在本章中研究的结构仅依赖于第1.4节中概述的第一和第三原则。也就是说,使用了精确的数学定义并给出了严格的证明,但不必依赖任何未经证实的计算假设。避免这种假设显然是有利的;然而,我们将看到,这样做有其固有的局限性。因此,除了作为理解现代密码学基本原理的良好基础外,本章的结果也证明了我们后来采用上述三个原理的合理性。
2.1 完美保密的定义
我们想象一个对手知道M的概率分布;也就是说,对手知道不同的消息将被发送的可能性。对手也知道正在使用的加密方案。对手唯一不知道的是双方共享的密钥。消息由诚实的一方选择并加密,由此产生的密文被传输给另一方。对手可以窃听双方的通信,从而观察这个密文。(也就是说,这是一种唯密文攻击,攻击者只看到一个密文。)对于一个完全秘密的计划,观察这个密文应该不会对对手关于实际发送的信息的知识产生影响;换句话说,以观察到的密文为条件,某些信息m∈M被发送的后验概率,应该与m被发送的先验概率没有什么不同。这意味着密文没有揭示潜在的明文,对手对加密的明文也一无所知。
DEFINITION 2.3 完美保密加密方案的定义
一个在明文空间M上的加密方案(Gen,Enc,Dec),如果对于每个明文 m ∈ M,对每个密文c ∈ C,其中Pr[C=c]>0,有:
Pr[ M = m | C = c ] = Pr[ M = m ]
则称这种加密方案是完美保密
LEMMA 2.5 完美保密方案的等价定义(一)
一个在明文空间M上的加密方案是完美保密的,当且仅当,对于每个明文m,m‘ ∈ M,以及每个密文 c ∈ C有:(即加密不同的明文得到相同的密文的概率是一样的,这个概率是通过遍历密钥空间得出来的)
证明引理2.5与定义2.3等价
等价性的证明需要两个方向分别证明
我们先证明定义2.3可以推出引理2.5
我们先来证明A式:
Pr[C = c | M = m]= Pr[Enck(m) = c]

我们来逐行解释一下。
第一行的等式,是由于C的定义
第二行的等式,是我们把M=m当做条件使用
第三行的等式,是因为密钥K的选取和密文M无关
对于Pr[C = c] > 0 (any c ∈ C),根据联合概率的两种拆解方式,我们还可以得到B式:
取M上的均匀分布。如果该方案是完美保密的,那么有Pr[M = m | C = c] = Pr[M = m],带入B式子,得到C式
Pr[C = c | M = m] = Pr[C = c]
由于m和c是任意的,这表明对于每一个m,m'∈M和每一个c∈M,有

我们来逐行解释一下。
第一行的等式,是逆用了A式
第二行的等式,是使用了C式
第三行的等式,是逆用了C式和使用了A式
我们再证明引理2.5可以推出定义2.5
我们假设上面的式子对于每个m, m’∈M 和每个c∈C都成立,记为D式
我们假设 Pr[M = m] > 0
对于c ∈ C,我们定义
记为E式
我们联立A、D、E式,得到F式
F式对于每一个m’∈M均成立,我们有

我们来逐行解释一下
第一行使用了全概率公式
第二行使用了F式,第二个等号利用了F式中m的任意性
这样我们就由引理2.5推出了定义2.5
完美不可区分性
完美保密的另一个等价定义。这个定义是基于一个实验,即对手被动地观察一个密文,然后试图猜测两条可能的消息中哪一条被加密了。我们引入了这个概念,因为它将作为我们在下一章中定义计算安全性的起点;在本书的其余部分中,我们将经常使用像这样的实验来定义安全性。
在目前的情况下,我们考虑以下实验:一个对手A首先指定两个任意的消息m0,m1∈M。接下来,使用Gen生成一个密钥k。然后,选择A指定的两条消息中的一条(概率为1/2),使用k加密;结果密文给A,最后输出“猜测”哪条消息被加密;如果猜测正确,则成功。如果没有一个对手A成功的概率大于1/2,那么加密方案是完全无法区分的。我们强调,对A的计算能力没有施加任何限制。
假设 Π = (Gen, Enc, Dec)是一个具有消息空间M的加密方案。假设A是一个对手,它在形式上只是一个(有状态的)算法,我们可以假设它是确定性的而不失去一般性。
我们定义一个对于方案Π和敌手A的实验,记为

下面给出该实验的准确定义
不可区分实验 The adversarial indistinguishability experiment
![]()
- 敌手A输出一对明文m0,m1 ∈ M
- 运行Gen生成一个随机密钥k,并选择一个统一的bit b∈{0,1}。计算密文c←Enck(mb),并返回给A。我们将c称为挑战密文
- A输出一个比特b’
- 如果b’ = b,那么实验的输出为1。否则,实验的输出为0。如果实验的输出为1,那么我们就说敌手A成功了
DEFINITION 2.6 完美不可区分方案的定义
一个在明文空间M上的加密方案:Π = (Gen, Enc, Dec)是完美不可区分的,当且仅当对每个敌手A都有:
LEMMA 2.7 完美保密方案的等价定义(二)
一个加密方案 Π 是完美保密的,当且仅当它是完美不可区分的。
证明引理2.7与定义2.3等价
我们先证明可以由引理2.7推出定义2.3
首先,完美不可取分意味着

等价于Pr[M=m0 | C=c] = Pr[M=m1 | C=c] = 1/2
而M = {m0,m1} ,即,明文空间中只有m0和m1
因此Pr[M=m] = 1/2
因此Pr[M=m | C=c] = Pr[M=m]对于任意m∈M均成立
我们再证明可以由定义2.3推出引理2.7
我们已经证明过引理2.5等价于定义2.3
引理2.5表明
Pr[Enck(m0)] = Pr[Enck(m1)]
我们之前证明了A式成立:Pr[C = c | M = m]= Pr[Enck(m) = c]
因此Pr[C=c | M=m0] = Pr[C=c | M=m1]
我们使用贝叶斯公式,得到
Pr[M=m0 | C=c] Pr[C=c] / Pr[M=m0] = Pr[M=m1 | C=c]Pr[C=c] / Pr[M=m1]
消去等式两边的相同部分,得到
Pr[M=m0 | C=c] / Pr[M=m0] = Pr[M=m1 | C=c] / Pr[M=m1]
因为Pr[M=m0] = Pr[M=m1]
所以Pr[M=m0 | C=c] = Pr[M=m1 | C=c]
这样就证明了不可区分性
Example 2.8 证明维吉尼亚密码体制不满足完美不可区分
设 Π 为两个长度为 2 的字符串的明文空间上的维基尼尔加密方案,并且密钥周期概率均匀地在{1,2}中选择。
敌手 A 的实验策略:输出两条明文m0 = aa,m1 = ab
对于返回的密文c = c1c2,敌手的输出策略为:如果c1 = c2,则输出 0 (即认为被加密的明文是m0);否则输出 1
敌手 A 实验成功的概率:

其中,b是决定哪个消息被加密的统一位
分两种情况进行讨论:
M=m0,即b=0时:
如果密钥的周期为1,那么c1 = c2,根据敌手的策略,敌手输出 0 的概率为1
如果密钥的周期为2,那么只有当密钥的第一个字母和第二个字母恰好相等的情况下敌手才能输出 0 ,即在这种情况下敌手输出 0 的概率为1/26
因此
M=m1,即b=1时:
那么只有当密钥的周期为2,并且密钥的第二个字母恰好比第一个字母小 1 的时候,敌手才会输出 0
我们把两种情况的概率相加,得到
因此,这个方案并不是完全无法区分的。




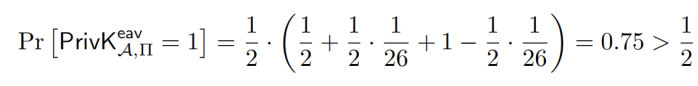





![BUUCTF Reverse/[GXYCTF2019]simple CPP](https://img-blog.csdnimg.cn/eb07f46c30c3402eb0e34012b251689c.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L29va2FtaTY0OTc=,size_16,color_FFFFFF,t_70#pic_center)