1.算法概述

2.仿真效果预览

3.MATLAB部分代码预览

4.完整MATLAB程序

1.算法概述

载波跟踪环是传统独立式GPS接收机最脆弱的环节，针对弱信号环境下其比伪码跟踪环路更容易失锁的问题，给出一种基于矢量频率锁定环（vector-frequency lock loop，VFLL）的载波跟踪方法。给出VFLL理论推导及实现过程，并以最小二乘估计方法证明VFLL在载波跟踪性能上优于频率锁定环（frequency lock loop，FLL）。静止场景时9颗卫星实验结果显示，本文给出的方法能够实现14 dB/Hz微弱GPS信号的载波跟踪。矢量型GPS信号跟踪算法（矢量延迟锁定环VDLL）

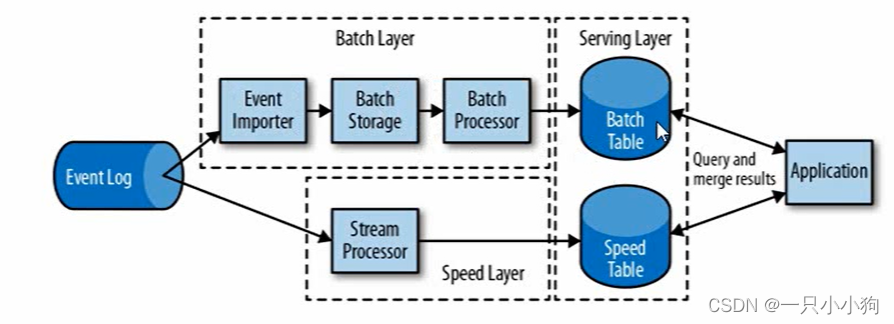
而在VDLL中，仅仅在DLL中对码跟踪进行改进，使其通过中心滤波器，而载波跟踪和传统的算法相同。所以，下面将重点对延迟锁定环进行改进，也就是你的课题的VDLL延迟锁定环。而VDFLL则是对码和载波分别进行改进。其基本结构如下所示：

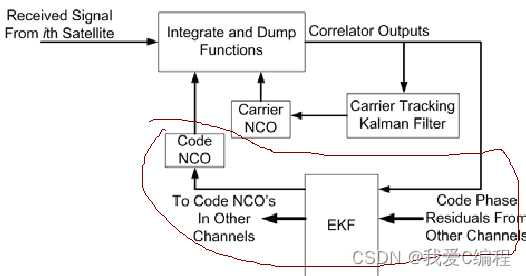
即使用卡尔曼替代PLL，使用EKF替代DLL。这个是VDFLL，而VDLL则使用扩展卡尔曼滤波替代原DLL即可。

提出的VDLL(vector delay lock loop)方法直接估计用户位置信息,由于用户物理动态有限,与传统的独立通道码环相比,跟踪的维度和带宽都更小,所以该方法具有更强的鲁棒性.阐述了VDLL与传统独立通道码跟踪环的本质区别,建立了VDLL的非线性系统模型,推导了系统观测量与传输延迟估计误差的具体线性化关系,确立了观测误差方差矩阵的计算公式;然后对非线性系统模型进行线性化,给出了多卫星联合跟踪下用户位置更新的EKF(extended Kalman filte-ring)滤波算法.

EKF

扩展卡尔曼滤波（Extended Kalman Filter，EKF）是标准卡尔曼滤波在非线性情形下的一种扩展形式，它是一种高效率的递归滤波器（自回归滤波器）。EKF的基本思想是利用泰勒级数展开将非线性系统线性化，然后采用卡尔曼滤波框架对信号进行滤波，因此它是一种次优滤波。

标准卡尔曼滤波KF的状态转移方程和观测方程为

${{\mathbf{\theta }}_{k}}=\mathbf{A}{{\mathbf{\theta }}_{k-1}}+\mathbf{B}{{\mathbf{u}}_{k-1}}+{{\mathbf{s}}_{k}}$

${{\mathbf{z}}_{k}}=\mathbf{C}{{\mathbf{\theta }}_{k}}+{{\mathbf{v}}_{k}}$

扩展卡尔曼滤波EKF的状态转移方程和观测方程为

${{\mathbf{\theta }}_{k}}=f({{\mathbf{\theta }}_{k-1}})+{{\mathbf{s}}_{k}}$ （1）

${{\mathbf{z}}_{k}}=h({{\mathbf{\theta }}_{k}})+{{\mathbf{v}}_{k}}$ （2）

利用泰勒展开式对（1）式在上一次的估计值处展开得

${{\mathbf{\theta }}_{k}}=f({{\mathbf{\theta }}_{k-1}})+{{\mathbf{s}}_{k}}=f(\left\langle {{\mathbf{\theta }}_{k-1}} \right\rangle )+{{\mathbf{F}}_{k-1}}\left( {{\mathbf{\theta }}_{k-1}}-\left\langle {{\mathbf{\theta }}_{k-1}} \right\rangle \right)+{{\mathbf{s}}_{k}}$ （3）

再利用泰勒展开式对（2）式在本轮的状态预测值处展开得

${{\mathbf{z}}_{k}}=h({{\mathbf{\theta }}_{k}})+{{\mathbf{v}}_{k}}=h\left( \mathbf{\theta }_{{k}}^{\mathbf{'}} \right)+{{\mathbf{H}}_{k}}\left( {{\mathbf{\theta }}_{k}}-\mathbf{\theta }_{{k}}^{\mathbf{'}} \right)+{{\mathbf{v}}_{k}}$ （4）

其中， ${\mathbf{F}}_{k-1}$ 和 ${\mathbf{H}}_{k}$ 分别表示函数 $f(\mathbf{\theta })$ 和 $h(\mathbf{\theta })$ 在 $\left\langle {{\mathbf{\theta }}_{k-1}} \right\rangle$ 和 $\mathbf{\theta }_{k}^{'}$ 处的雅克比矩阵。

（注：这里对泰勒展开式只保留到一阶导，二阶导数以上的都舍去，噪声假设均为加性高斯噪声）

基于以上的公式，给出EKF的预测（Predict）和更新（Update）两个步骤：

Propagation：

$\mathbf{\theta }_{k}^{'}=f(\left\langle {{\mathbf{\theta }}_{k-1}} \right\rangle)$

$\mathbf{\Sigma }_{k}^{'}=\mathbf{F}_{k-1}{{\mathbf{\Sigma }}_{k-1}}{{\mathbf{F}}_{k-1}^{T}}+\mathbf{Q}$

Update：

$\mathbf{S}_{k}^{'}={{\left( \mathbf{H_{k}\Sigma }_{k}^{'}{{\mathbf{H}}_{k}^{T}}+\mathbf{R} \right)}^{-1}}$

$\mathbf{K}_{k}^{'}=\mathbf{\Sigma }_{k}^{'}{{\mathbf{H}}_{k}^{T}}\mathbf{S}_{k}^{'}$

$\left\langle {{\mathbf{\theta }}_{k}} \right\rangle =\mathbf{\theta }_{k}^{'}+\mathbf{K}_{k}^{'}\left( {{\mathbf{z}}_{k}}-{h(\theta }_{k}^{'}) \right)$

${{\mathbf{\Sigma }}_{k}}=\left( \mathbf{I}-\mathbf{K}_{k}^{'}\mathbf{H}_{k} \right)\mathbf{\Sigma }_{k}^{'}$

其中的雅克比矩阵 ${\mathbf{F}}_{k-1}$ 和 ${\mathbf{H}}_{k}$ 分别为

${{\mathbf{F}}_{k-1}}={{\left. \frac{\partial f}{\partial \mathbf{\theta }} \right|}_{\left\langle {{\mathbf{\theta }}_{k-1}} \right\rangle }}$ ， ${{\mathbf{H}}_{k}}={{\left. \frac{\partial h}{\partial \mathbf{\theta }} \right|}_{\mathbf{\theta }_{k}^{'}}}$

雅可比矩阵的计算，在MATLAB中可以利用对自变量加上一个eps（极小数），然后用因变量的变化量去除以eps即可得到雅可比矩阵的每一个元素值。

2.仿真效果预览

matlab2022a仿真结果如下：

3.MATLAB部分代码预览

...............................................................
%参数初始化 
time      = 1000*(10^(-3));     % 数据发送时间
time_unit = 20*(10^(-3));      % 数据跳变时间单位
time_cyc  = 1*(10^(-3));       % 一个完整扩频码周期
fs        = 5*(10^6);
nn        = time_cyc*fs;
kk        = (time/time_cyc)*nn;% 数据总采样点
F_if      = 1.25*(10^6);       % 载波中频
F_Carrier = 1575.42*(10^6);    % L1波段载波频率
CA_freq   = 1.023*(10^6);      % CA码速率
 
%%
%%
%生成C/A码
PN = func_CAcodegen(svnum);
CA = [];
k  = 5;
for n = 1:length(PN)
    CA((1+k*(n-1)):k*n) = PN(n)*ones(1,k);%CA码扩展
end
tc                      = 1/(k*CA_freq); 
loop_time               = time/time_cyc;
 
%%
%%
%模拟产生测试信号源
[Signal_Source,Phase_signal,buffer_bit_data]=func_CreateSource(iniphcode,inifd,iniph,snr); 
 
%%
%%
%在模拟之前，首先需要进行捕获
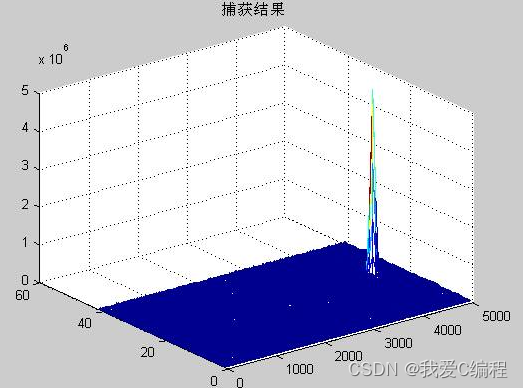
[fd_ac,f_ac_code,Corr_value] = func_acquire(Signal_Source);
figure
mesh(Corr_value);title('捕获结果');
 
%信号中断起始时间
break_start = 400;
break_end   = 800;
 
 
P0            = [0 0
                 0 1];
P             = [P0 zeros(2,2*(loop_time-1))];
T             = 0.1;
LL            = loop_time;
Y0            = [0;1];
data_out(:,1) = Y0;           %Y的第一列等于Y0
A             = [1 T
                 0 1];   
B             = [1/2*(T)^2 T]';
H             = [1 0];
Q             = (0.25)^2; 
R             = (0.25)^2; 
X             = zeros(1,loop_time);
    
      
%%
%%
%跟踪参数设置
tracking_parameter();
%进行跟踪
for i = 1:1:loop_time   
    
    i
 
    %开始循环，每次循环去除一段数据
    %开始循环，每次循环去除一段数据
    %模拟信号突然中断
    if i > break_start & i < break_end
    Signal = 0.0001*rand(1,nn);%中断的时候，该段数据为随机的噪声干扰
    else
    Signal = Signal_Source((i-1)*nn+1:i*nn);
    end
    
    %产生本地载波
    t                 = [0:nn-1]*ts;
    track_dopplar     = fd_ac + track_freq_pll;
    Track_Freq_Buffer = [Track_Freq_Buffer track_dopplar];
    track_dopplar2    = [track_dopplar2   track_freq_pll];
     
    Local_I           = cos(2*pi*(F_if+track_dopplar)*t + Last_Phase);
    Local_Q           = sin(2*pi*(F_if+track_dopplar)*t + Last_Phase);
    Iph               = 2*pi*(F_if+track_dopplar)*t + Last_Phase;
    Local_Ph_Buffer   = [Local_Ph_Buffer Iph];
    Last_Phase        = Last_Phase + 2*pi*(F_if+track_dopplar)*time_cyc;   
 
    
    %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
    Carrier_I         = Local_I;%产生本地的载波
    Carrier_Q         = Local_Q;%产生本地的载波
    
 
 
    %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
    %产生本地相位码
    %利用DLL的思路
    %当前
    ph_code_p = offside;
    fd_code_p = track_dopplar;
    CA_Code_p = func_CA(ph_code_p,fd_code_p,i);
    lc_p      = CA_Code_p.*Signal;
    %早
    ph_code_e = offside+diffoffside;
    fd_code_e = track_dopplar;
    CA_Code_e = func_CA(ph_code_e,fd_code_e,i);
    lc_e      = CA_Code_e.*Signal;        
    %迟
    ph_code_l = offside-diffoffside;
    fd_code_l = track_dopplar;
    CA_Code_l = func_CA(ph_code_l,fd_code_l,i);
    lc_l      = CA_Code_l.*Signal;
 
    %下变频
    Local_P_I = lc_p.*Carrier_I;
    Local_P_Q = lc_p.*Carrier_Q;
    Local_E_I = lc_e.*Carrier_I;
    Local_E_Q = lc_e.*Carrier_Q;
    Local_L_I = lc_l.*Carrier_I;
    Local_L_Q = lc_l.*Carrier_Q;
 
    
    
    %积分运算
    IPSum     = sum(Local_P_I);
    QPSum     = sum(Local_P_Q);
    IESum     = sum(Local_E_I);
    QESum     = sum(Local_E_Q);
    ILSum     = sum(Local_L_I);
    QLSum     = sum(Local_L_Q);
    
 
 
    
    
    %码相位环路控制
    %鉴想器 
    theta_code        = ((IESum.^2+QESum.^2)-(ILSum.^2+QLSum.^2))/((IESum.^2+QESum.^2)+(ILSum.^2+QLSum.^2));
     
    I2_Q2(i)          = IESum.^2 + QESum .^2;
     
    %kalman
    data(:,i)       = theta_code;
    j               = (i-1)*2+1;
    K               = P(:,j:j+1)*H'*inv(H*P(:,j:j+1)*H'+R);%滤波增益
    data_out(:,i)   = data_out(:,i)+K*(data(1,1)-H*data_out(:,i));  %估计
    data_out(:,i+1) = A*data_out(:,i);                     %预测
    P(:,j:j+1)      = (eye(2,2)-K*H)*P(:,j:j+1);  %误差
    P(:,j+2:j+3)    = A*P(:,j:j+1)*A'+B*Q*B';   %kalman滤波
 
    CodeErr         = data_out(1,i)/20;
    
    
    %码环NCO
    offside           = offside_old+k1*CodeErr;      %码NCO的输出
 
    theta_code_old    = theta_code;  %将当前结果保存，用于下一个循环的码跟踪
    CodeErr_old       = CodeErr;        %将当前结果保存，用于下一个循环的码跟踪
    offside_old       = offside;        %将当前结果保存，用于下一个循环的码跟踪
    Bk_DLL            = [Bk_DLL theta_code];   %记录跟踪过程中的码环鉴想器的输出
    Track_Code_Buffer = [Track_Code_Buffer offside];  %记录跟踪过程中的码环NCO的数出
   
    
    %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
 
 
    %载波跟踪
    %载波跟踪
    %载波跟踪
    theta_pll      = atan(QPSum/IPSum);
    PLLinput       = theta_pll/(2*pi*time_cyc);
    Bk_PLL         = [Bk_PLL theta_pll];
 
    %LoopFilter       
    PLLoutput      = func_CarLoopFilter(carrierw,carrierpllb/2,PLLinput,PLLinput_old,PLLoutput_old); 
 
    track_freq_pll = -PLLoutput;
 
    PLLinput_old   = PLLinput;       
    PLLoutput_old  = PLLoutput;       
 
    adj_flag          = track_dopplar - track_dopplar_old; 
    track_dopplar_old = track_dopplar; 
    adj_buffer        = [adj_buffer adj_flag];
      
    outdata           = sign(real(IPSum)); 
    ALL_Buffer_Data   = [ALL_Buffer_Data outdata];
          
    if adj_flag < 1      
       add = add+1;
    else
       add = 0;
    end
    if add >= 2          
       dem_flag = 1;
    end
    
    if dem_flag == 1
       count_time   = i;
       count_buffer = [count_buffer count_time];
       Buffer_Data  = [Buffer_Data outdata];
    end
end
 
%%
%%
%位同步与数据解调
Buffer_Data_out = func_bitssync(Buffer_Data,count_buffer);  
l_i_d           = time/time_unit;
l_o_d           = length(Buffer_Data_out);
l_zeros         = l_i_d - l_o_d;
Buffer_Data_out = [zeros(1,l_zeros) Buffer_Data_out]; 
 
%跟踪误差
l_dll     = length(Track_Code_Buffer);
l_fll     = length(Track_Freq_Buffer);
diata_dll = (Track_Code_Buffer(40:l_dll)-iniphcode);  
  
break_start = 400;
break_end   = 800;
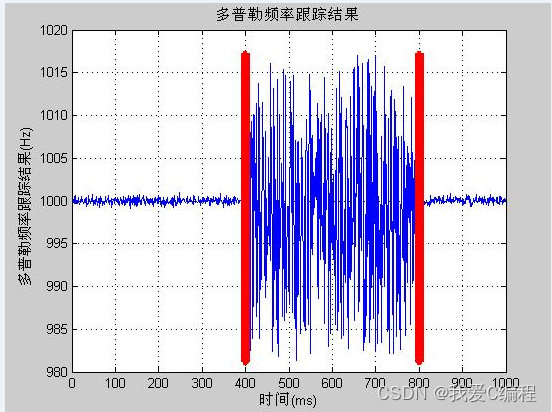
%多普勒频率跟踪
figure;
plot(Track_Freq_Buffer);
xlabel('时间(ms)');
ylabel('多普勒频率跟踪结果(Hz)')
title('多普勒频率跟踪结果');
grid on
hold on
 
plot(break_start,min(Track_Freq_Buffer):0.01:max(Track_Freq_Buffer),'r-*','LineWidth',3);hold on
plot(break_end,min(Track_Freq_Buffer):0.01:max(Track_Freq_Buffer),'r-*','LineWidth',3);hold off
 
 
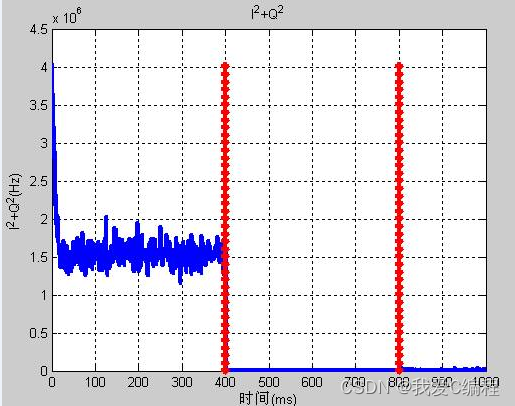
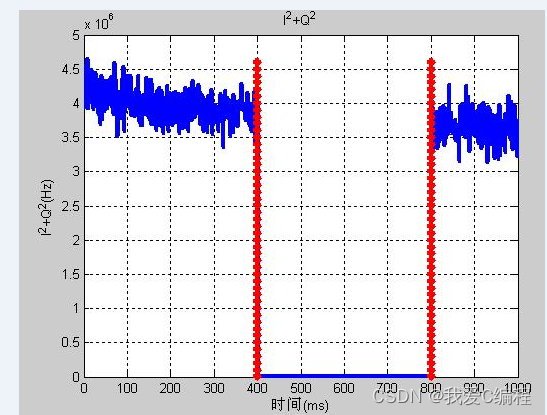
figure;
plot(I2_Q2(1:end),'LineWidth',3);
xlabel('时间(ms)');
ylabel('I^2+Q^2(Hz)')
title('I^2+Q^2');
grid on
hold on
 
plot(break_start,min(I2_Q2(1:end)):100000:max(I2_Q2(1:end)),'r-*','LineWidth',3);hold on
plot(break_end,min(I2_Q2(1:end)):100000:max(I2_Q2(1:end)),'r-*','LineWidth',3);hold off
 
 
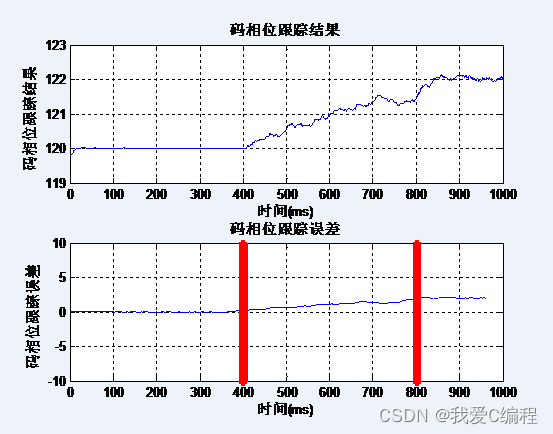
%码相位跟踪
figure;
subplot(211);
plot(Track_Code_Buffer);
xlabel('时间(ms)');
ylabel('码相位跟踪结果');
title('码相位跟踪结果');
grid on
axis([0,length(Track_Code_Buffer),0.8*iniphcode,1.2*iniphcode]);
subplot(212);
plot(diata_dll);
xlabel('时间(ms)');
ylabel('码相位跟踪误差');
title('码相位跟踪误差');
grid on
axis([0,length(diata_dll),-10,10]); 
hold on
 
plot(break_start,-10:0.1:10,'r-*','LineWidth',3);hold on
plot(break_end,-10:0.1:10,'r-*','LineWidth',3);hold off
01_048_m