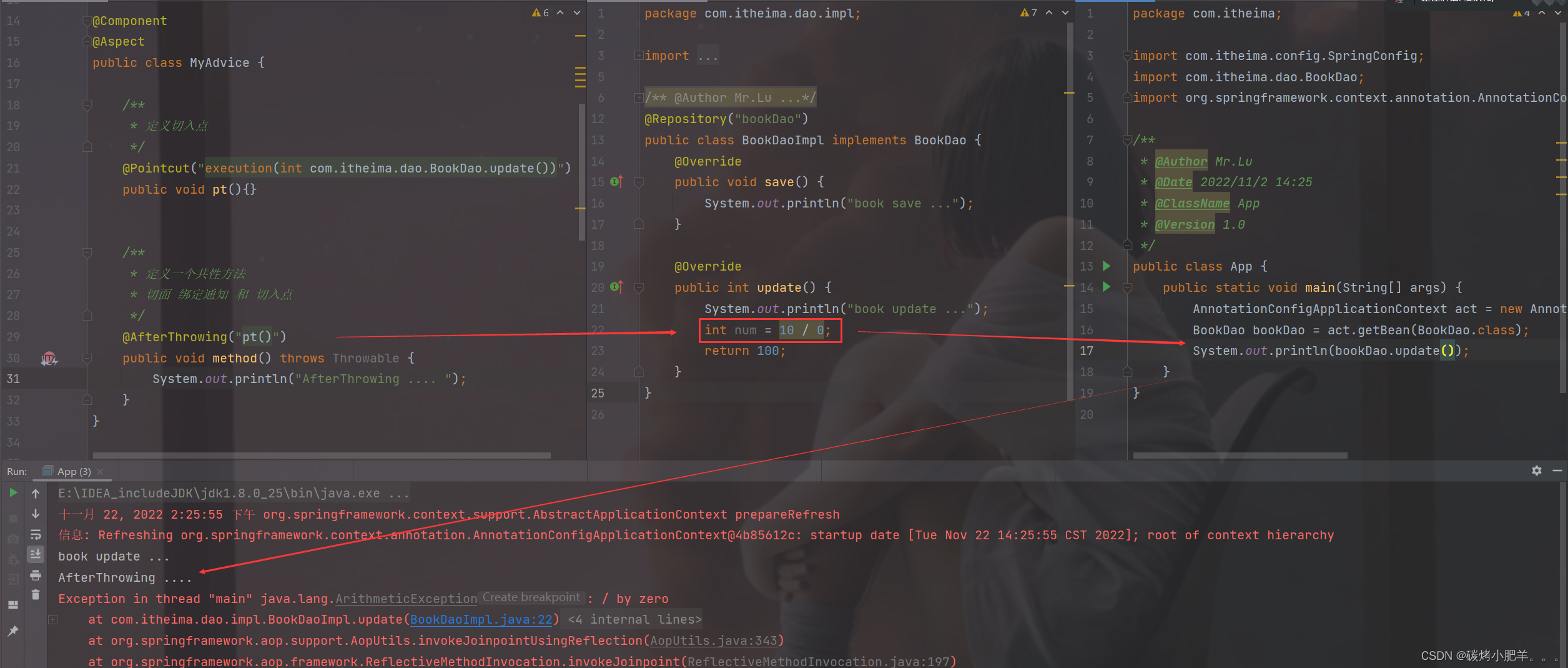
两种情况
1. 数据集有正负样本，但正样本的量远远大于负样本为异常检测，即大量的正样本为正常，少数的负样本是异常的。
2. 数据集只有正样本，称为单分类，即只通过正样本训练模型，区分正样本和非正样本。
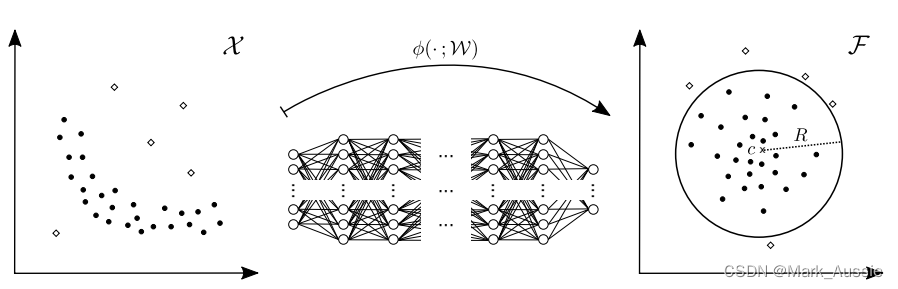
情况一
左是原始的数据，图中有两种--白点和黑点，做异常检测（abnormal detection），假设数据的特征向量是二维的，左边是一个输入空间，假设要将黑点（正）和白点（负）的数据分类。Deep-SVDD 就是训练一个神经网络，将输入的数据变成右边的一个输出空间，对新的数据，经过模型之后，新数据落在了圆心为c,半径为R的圆（高维空间就叫超球面）里面，就认为是黑点（正样本），反之落在圆外就认为是白点（负样本）这样，就得到了一个分类模型，可以区分黑白点了。
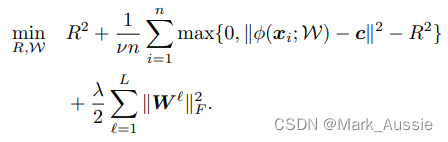
Deep-SVDD软边界目标函数
数据含有异常数据，且没有标签，假设是黑点之间都是非常相似的，且和白点有一定的区别，但是不能直接找出这种区别，需要通过模型分类。
minRW：全局最小化整个公式，参数是R 和 W；最小化R的平方，相当于最小R，就是要尽量把半径缩小，尽量把所有的黑点放在一个圈里，将白点远离圈，区分黑白点，半径为区分阈值。
，惩罚项，
大于 0 时，有些数据点落在了圈外，整个式子的值就会变大，优化时会尽量将所有的数据点位于圈内；又因为有异常值存在，所以应该有一些点落在圈外，因而添加 1/vn，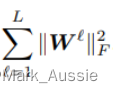
隐藏层的正则化，λ为超参数。
情况二
单分类，训练数据没有异常样本，都属于一个类，
目标函数为
，所有数据靠近球心，得分函数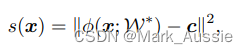
，c 为球心。
参考：
Deep-SVDD论文研读 - 知乎
GitHub - lukasruff/Deep-SVDD-PyTorch: A PyTorch implementation of the Deep SVDD anomaly detection method
http://data.bit.uni-bonn.de/publications/ICML2018.pdf
