小尼在这里跟大家说明一下0-1背包问题的理论，首先我们需要认识一下什么是背包问题。小尼在这里拉一下代码随想录的代码，有兴趣的小伙伴也想把背包问题学好，可以去代码随想录看一看背包问题的讲解，也可以去B站看一看代码随想录对背包问题的讲解：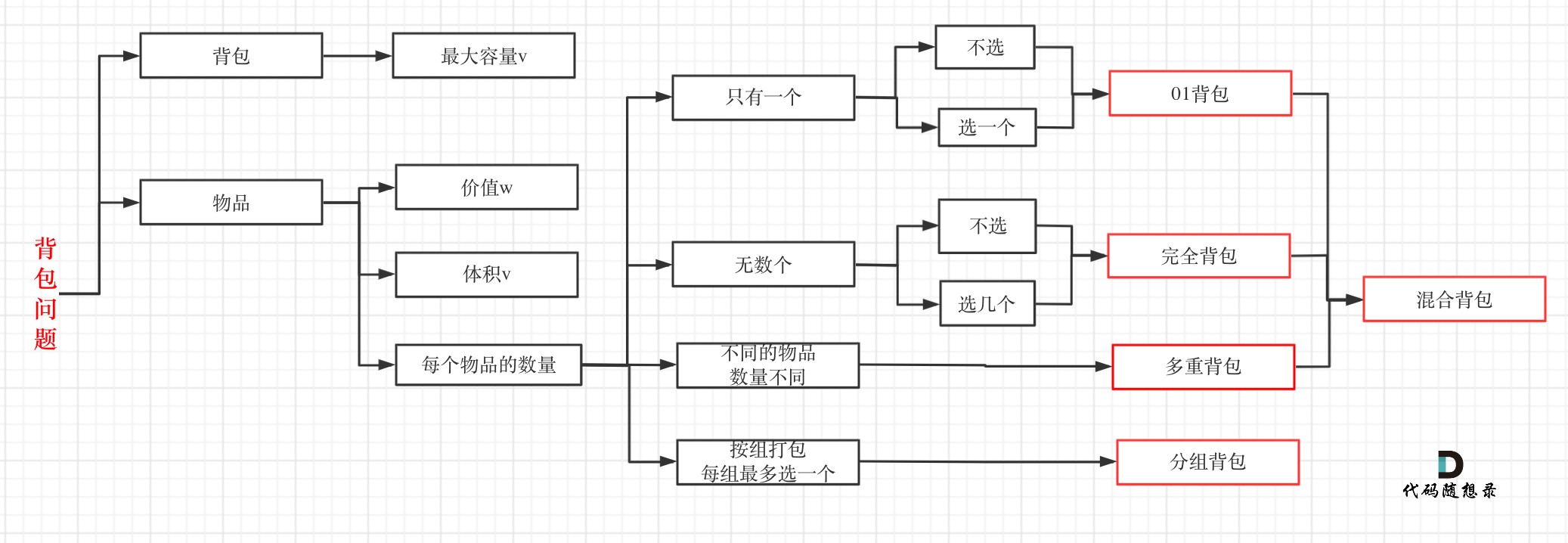

有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。

这是标准的背包问题，以至于很多同学看了这个自然就会想到背包，甚至都不知道暴力的解法应该怎么解了。

这样其实是没有从底向上去思考，而是习惯性想到了背包，那么暴力的解法应该是怎么样的呢？

每一件物品其实只有两个状态，取或者不取，所以可以使用回溯法搜索出所有的情况，那么时间复杂度就是$o(2^n)$，这里的n表示物品数量。

所以暴力的解法是指数级别的时间复杂度。进而才需要动态规划的解法来进行优化！

我们既然将背包问题当成动态规划的问题进行对应的求解，那么我们就一定存在递归五部曲，小尼一一说明一下这五部的进行，首先第一步：确定dp数组以及下标的含义

对于背包问题，我们先讲第一种写法，就是利用二维数组，即dp[i][j]表示从下表为[0-i]的物品里面任意取，放进容量为j的背包里面，价值总和的最大是多少，所以小伙伴一定要搞清楚，dp在这里表示的是价值的多少，也就是在i,j同时满足的条件下得到的价值的最优解

第二步：递推公式

我们回顾一下dp数组的含义，就是从下标为[0-i]的物品里面任意取，放进容量为j的背包，价值总和最大时多少，我们先需要分析放入的情况：

1、我们不放入物品：由dp[i-1][j]推出，即背包容量为j，里面不放入物品i的最大价值，此时dp[i][j]就是dp[i-1][j]。（其实就是当物品i的重量大于背包j的重量时，物品i无法放入背包中，所以背包内的价值依然和前面的相同）

2、我们放入物品：由dp[i-1][j-weight[i]]可以推出，dp[i-1][j-weight[i]]为背包容量为j-weight[i]的时候不放入物品i的最大价值，那么dp[i-1][j-weight[i]] + value[i]（物品i的价值），就是背包放物品i得到的最价值，所以递归的公式为：dp[i][j] = max(dp[i-1][j], dp[]i-1[j-weight[i]] + value[i])

第三步：对dp数组进行初始化

首先我们从dp[i][j]的定义出发，如果背包容量j为0的话，即dp[i][0]，无论是选取哪些物品，背包价值总和一定为0。对于小尼所说的上述的二维数组的情况也只需要给出这一个初始化就可以了。

第四步：确定遍历顺序

在本层的条件下，我们无论是从物品的角度进行遍历或者是从背包容量的大小进行遍历都是可以的。小尼接下来就给出先遍历物品，然后遍历背包重量的代码：

// weight数组的大小 就是物品个数
for(int i = 1; i < weight.size(); i++) { // 遍历物品
    for(int j = 0; j <= bagweight; j++) { // 遍历背包容量
        if (j < weight[i]) dp[i][j] = dp[i - 1][j]; 
        else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);

    }
}

小尼接下来再给出先遍历背包，再遍历物品的代码：

// weight数组的大小 就是物品个数
for(int j = 0; j <= bagweight; j++) { // 遍历背包容量
    for(int i = 1; i < weight.size(); i++) { // 遍历物品
        if (j < weight[i]) dp[i][j] = dp[i - 1][j];
        else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
    }
}

第五步：导出背包放入的顺序

最后我们只需要导出顺序即可

小尼接下来给出一段一个背包的完整的代码：

public static void main(String[] args) {
        int[] weight = {1, 3, 4};
        int[] value = {15, 20, 30};
        int bagsize = 4;
        testweightbagproblem(weight, value, bagsize);
    }

    public static void testweightbagproblem(int[] weight, int[] value, int bagsize){
        int wlen = weight.length, value0 = 0;
        //定义dp数组：dp[i][j]表示背包容量为j时，前i个物品能获得的最大价值
        int[][] dp = new int[wlen + 1][bagsize + 1];
        //初始化：背包容量为0时，能获得的价值都为0
        for (int i = 0; i <= wlen; i++){
            dp[i][0] = value0;
        }
        //遍历顺序：先遍历物品，再遍历背包容量
        for (int i = 1; i <= wlen; i++){
            for (int j = 1; j <= bagsize; j++){
                if (j < weight[i - 1]){
                    dp[i][j] = dp[i - 1][j];
                }else{
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weight[i - 1]] + value[i - 1]);
                }
            }
        }
        //打印dp数组
        for (int i = 0; i <= wlen; i++){
            for (int j = 0; j <= bagsize; j++){
                System.out.print(dp[i][j] + " ");
            }
            System.out.print("\n");
        }
    }