2465. 不同的平均值数目
给你一个下标从 0 开始长度为 偶数 的整数数组 nums 。
只要 nums 不是 空数组,你就重复执行以下步骤:
- 找到
nums中的最小值,并删除它。 - 找到
nums中的最大值,并删除它。 - 计算删除两数的平均值。
两数 a 和 b 的 平均值 为 (a + b) / 2 。
- 比方说,
2和3的平均值是(2 + 3) / 2 = 2.5。
返回上述过程能得到的 不同 平均值的数目。
注意 ,如果最小值或者最大值有重复元素,可以删除任意一个。
提示
2 <= nums.length <= 100nums.length是偶数。0 <= nums[i] <= 100
示例
输入:nums = [4,1,4,0,3,5]
输出:2
解释:
1. 删除 0 和 5 ,平均值是 (0 + 5) / 2 = 2.5 ,现在 nums = [4,1,4,3] 。
2. 删除 1 和 4 ,平均值是 (1 + 4) / 2 = 2.5 ,现在 nums = [4,3] 。
3. 删除 3 和 4 ,平均值是 (3 + 4) / 2 = 3.5 。
2.5 ,2.5 和 3.5 之中总共有 2 个不同的数,我们返回 2 。
思路
简单模拟
先排序,然后用双指针进行模拟,并用set去重。
// C++
class Solution {
public:
int distinctAverages(vector<int>& nums) {
unordered_set<int> s;
sort(nums.begin(), nums.end());
int i = 0, j = nums.size() - 1;
while (i < j) {
s.emplace(nums[i] + nums[j]); // 不需要算平均值
i++;
j--;
}
return s.size();
}
};
2466. 统计构造好字符串的方案数
给你整数 zero ,one ,low 和 high ,我们从空字符串开始构造一个字符串,每一步执行下面操作中的一种:
- 将
'0'在字符串末尾添加zero次。 - 将
'1'在字符串末尾添加one次。
以上操作可以执行任意次。
如果通过以上过程得到一个 长度 在 low 和 high 之间(包含上下边界)的字符串,那么这个字符串我们称为 好 字符串。
请你返回满足以上要求的 不同 好字符串数目。由于答案可能很大,请将结果对 10^9 + 7 取余 后返回。
提示:
1 <= low <= high <= 10^51 <= zero, one <= low
示例
输入:low = 3, high = 3, zero = 1, one = 1
输出:8
解释:
一个可能的好字符串是 "011" 。
可以这样构造得到:"" -> "0" -> "01" -> "011" 。
从 "000" 到 "111" 之间所有的二进制字符串都是好字符串。
思路
本质是个组合问题,可以将问题抽象成这样:x初始为0,每次操作可以选择加上zero或者one,问经过若干次操作后,能使得x位于[low, high]区间内,总的操作方案数。
周赛当晚,最直观的想法当然就是暴力枚举了。然而由于最大的数据是low = 1,high = 10^5,zero = one = 1,每次有2个选择,而一共可以做10^5次选择,那么总的时间复杂度就能达到
2
1
0
5
2^{10^5}
2105,这超时都超到太阳系外边去了。肯定是不行的。
// C++
const int MOD = 1e9 + 7;
class Solution {
public:
int ans = 0;
void dfs(int i, int z, int o, int low, int high) {
if (i > high) return ;
if (i >= low && i <= high) {
ans++;
ans = ans % MOD;
}
// 填0
dfs(i + z, z, o, low, high);
// 填1
dfs(i + o, z, o, low, high);
}
int countGoodStrings(int low, int high, int zero, int one) {
dfs(0, zero, one, low, high);
return ans;
}
};
看着这种每次加上一个数,有点动态规划那意思。于是就往动态规划上面想。
状态 f[i]表示,构造出的字符串长度为i时的总方案数。
接下来看状态转移,因为状态转移肯定跟某一次我们的选择有关系,而我们每次有2种选择。所以我们将状态数组开成二维,用f[i][0]表示,最后一次选择的是zero,且构造出的字符串长度为i时的方案数;f[i][1]表示,最后一次选择是one。
对于f[i][0],由于最后一次选择的是zero,则我们最后一次选择之前,得到的字符串长度是i - zero,所以f[i][0] = f[i - zero][0] + f[i - zero][1]
同理,有f[i][1] = f[i - one][0] + f[i - one][1]
// C++
const int MOD = 1e9 + 7;
class Solution {
public:
int countGoodStrings(int low, int high, int zero, int one) {
vector<vector<int>> f(high + 10, vector<int>(2, 0));
f[zero][0] = f[one][1] = 1;
long long ans = 0;
for (int i = 1; i <= high; i++) {
if (i - zero > 0) {
f[i][0] = (f[i - zero][0] + f[i - zero][1]) % MOD;
}
if (i - one > 0) {
f[i][1] = (f[i - one][0] + f[i - one][1]) % MOD;
}
if (i >= low && i <= high) {
ans += f[i][0] + f[i][1];
ans = ans % MOD;
}
}
return (int) ans;
}
};
上面的代码还能优化,这里就不再赘述。
其实这道题就是爬楼梯。😓
2467. 树上最大得分和路径
一个 n 个节点的无向树,节点编号为 0 到 n - 1 ,树的根结点是 0 号节点。给你一个长度为 n - 1 的二维整数数组 edges ,其中 edges[i] = [ai, bi] ,表示节点 ai 和 bi 在树中有一条边。
在每一个节点 i 处有一扇门。同时给你一个都是偶数的数组 amount ,其中 amount[i] 表示:
- 如果
amount[i]的值是负数,那么它表示打开节点i处门扣除的分数。 - 如果
amount[i]的值是正数,那么它表示打开节点i处门加上的分数。
游戏按照如下规则进行:
-
一开始,Alice 在节点
0处,Bob 在节点bob处。 -
每一秒钟,Alice 和 Bob 分别 移动到相邻的节点。Alice 朝着某个 叶子结点 移动,Bob 朝着节点
0移动。 -
对于他们之间路径上的
每一个
节点,Alice 和 Bob 要么打开门并扣分,要么打开门并加分。注意:
- 如果门 已经打开 (被另一个人打开),不会有额外加分也不会扣分。
- 如果 Alice 和 Bob 同时 到达一个节点,他们会共享这个节点的加分或者扣分。换言之,如果打开这扇门扣
c分,那么 Alice 和 Bob 分别扣c / 2分。如果这扇门的加分为c,那么他们分别加c / 2分。
-
如果 Alice 到达了一个叶子结点,她会停止移动。类似的,如果 Bob 到达了节点
0,他也会停止移动。注意这些事件互相 独立 ,不会影响另一方移动。
请你返回 Alice 朝最优叶子结点移动的 最大 净得分。
提示:
2 <= n <= 10^5edges.length == n - 1edges[i].length == 20 <= ai, bi < nai != biedges表示一棵有效的树。1 <= bob < namount.length == namount[i]是范围[-10^4, 10^4]之间的一个 偶数 。
示例
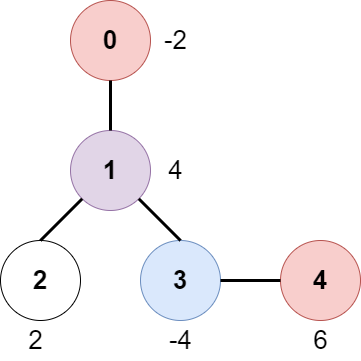
输入:edges = [[0,1],[1,2],[1,3],[3,4]], bob = 3, amount = [-2,4,2,-4,6]
输出:6
解释:
上图展示了输入给出的一棵树。游戏进行如下:
- Alice 一开始在节点 0 处,Bob 在节点 3 处。他们分别打开所在节点的门。
Alice 得分为 -2 。
- Alice 和 Bob 都移动到节点 1 。
因为他们同时到达这个节点,他们一起打开门并平分得分。
Alice 的得分变为 -2 + (4 / 2) = 0 。
- Alice 移动到节点 3 。因为 Bob 已经打开了这扇门,Alice 得分不变。
Bob 移动到节点 0 ,并停止移动。
- Alice 移动到节点 4 并打开这个节点的门,她得分变为 0 + 6 = 6 。
现在,Alice 和 Bob 都不能进行任何移动了,所以游戏结束。
Alice 无法得到更高分数。
思路
两次遍历
因为Alice到达叶子节点有多种路径,但Bob到达0节点只有一种路径,当Alice到达某个节点时,我们需要知道,在这一时刻,Bob与这一节点的关系,无外乎下面三种
Bob也恰好在这一时刻到达这一节点Bob在这一时刻之前已经到达过这一节点Bob还未到达过这一节点
所以,我们先通过一次遍历,找到Bob的移动路径,并且对于这条路径上的每个节点,我们都能求出其与Bob起始节点之间的距离(其实就代表了Bob是在哪一个时刻到达该节点的)。随后,我们再进行一次遍历,让Alice从0号点出发,通过DFS遍历整个树,在经过每个节点时,我们容易得知当前节点与0号节点之间的距离,故而能判断此时Bob是否到达该节点,并能算出Alice到达该节点的得分。遍历到叶子节点时,即找到一条可能的路径,用该路径的累加得分来更新答案即可。
// C++
const int N = 1e5 + 10, M = 2 * N;
class Solution {
public:
// 树的邻接表表示
int h[N], e[M], ne[M], idx;
int p[N]; // 父亲节点
int b[N]; //被bob访问过的那些节点, 的时间, 如 b[1] = 3, 表示bob将在第3秒钟时, 访问1号节点, 若b[i] = -1 说明该节点不会被bob访问
bool st[N]; // 用来存储已经被alice访问过的节点, 不能走回头路
vector<int> amount;
int ans = -1e9;
// 深搜, 访问x节点时, 时间是time
void dfs(int x, int time, int score) {
st[x] = true; // 该节点已经被走过
// 如果bob不会访问这个节点, 或者在当前时间bob不会访问这个节点
// 直接加这个节点的贡献值
if (b[x] == -1 || time < b[x]) score += amount[x];
else if (time == b[x]) score += amount[x] / 2; // 刚好同时访问到这个节点, 加一半
// else if (time > b[x]) score += 0; // 该节点的已经被bob打开了, 不需要添加这个节点的贡献
// 是否到达叶子节点
bool is_leaf = true;
// 遍历子节点
for (int i = h[x]; i != -1; i = ne[i]) {
int u = e[i];
if (st[u]) continue;
is_leaf = false; // 只要有还能走的子节点, 则该节点不是叶子节点
dfs(u, time + 1, score);
}
if (is_leaf) {
// 是叶子节点了, 那么用score更新答案
ans = max(ans, score);
}
}
void add(int a, int b) {
e[idx] = b;
ne[idx] = h[a];
h[a] = idx++;
}
int mostProfitablePath(vector<vector<int>>& edges, int bob, vector<int>& amount) {
this->amount = amount;
memset(h, -1, sizeof h);
memset(b, -1, sizeof b);
memset(p, -1, sizeof p);
for (auto& e : edges) {
int a = e[0], b = e[1];
add(a, b);
add(b, a);
}
// 先用bfs求出根节点到bob的访问路径
queue<int> q;
q.push(0);
// 这里也暂时借用一下st数组
st[0] = true;
// 是否找到bob
bool end = false;
while (!q.empty()) {
int x = q.front();
q.pop();
for (int i = h[x]; i != -1; i = ne[i]) {
int u = e[i];
if (st[u]) continue;
p[u] = x;
q.push(u);
st[u] = true;
if (u == bob) {
end = true;
break;
}
}
if (end) break; // 找到bob了, 退出bfs
}
// 清空st
memset(st, false, sizeof st);
// 回溯, 沿着bob往上走, 将bob走过的节点依次赋值
for (int x = bob, i = 0; p[x] != -1; x = p[x], i++) b[x] = i;
// 从根节点开始深搜
dfs(0, 0, 0);
return ans;
}
};
2468. 根据限制分割消息
给你一个字符串 message 和一个正整数 limit 。
你需要根据 limit 将 message 分割 成一个或多个 部分 。每个部分的结尾都是 "<a/b>" ,其中 "b" 用分割出来的总数 替换, "a" 用当前部分所在的编号 替换 ,编号从 1 到 b 依次编号。除此以外,除了最后一部分长度 小于等于 limit 以外,其他每一部分(包括结尾部分)的长度都应该 等于 limit 。
你需要确保分割后的结果数组,删掉每部分的结尾并 按顺序 连起来后,能够得到 message 。同时,结果数组越短越好。
请你返回 message 分割后得到的结果数组。如果无法按要求分割 message ,返回一个空数组。
提示:
1 <= message.length <= 10^4message只包含小写英文字母和' '。1 <= limit <= 10^4
示例
输入:message = "this is really a very awesome message", limit = 9
输出:["thi<1/14>","s i<2/14>","s r<3/14>","eal<4/14>","ly <5/14>","a v<6/14>","ery<7/14>"," aw<8/14>","eso<9/14>","me<10/14>"," m<11/14>","es<12/14>","sa<13/14>","ge<14/14>"]
解释:
前面 9 个部分分别从 message 中得到 3 个字符。
接下来的 5 个部分分别从 message 中得到 2 个字符。
这个例子中,包含最后一个部分在内,每个部分的长度都为 9 。
可以证明没有办法分割成少于 14 个部分。
思路
这是一道挺恶心的模拟题。周赛当天我读题读了半天愣是没读懂。
是这个意思,给一个字符串message,尝试将其分为n部分,第一部分的字符串,在后面加上<1/n>,第二部分字符串在后面加上<2/n>,…
使得加上这个<a/b>后,每一部分字符串的长度都是limit(最后一部分的长度可以小于limit)。需要结果数组越短越好,就是n越小越好。
首先,原字符串message的长度是确定的,假设我们要分成n部分,那么每一部分都会多出一个<a/b>,总共n部分(b = n),多出的字符串长度总和是多少呢?容易发现,<a/b>中,只有a是变化的,其余部分都是固定的,除了a,其余部分的长度是3加上b的位数(也就是n的位数)。加上n一共有k位,那么这部分多出来的长度就是(3 + k) × n。然后我们再来看a,n部分所有a的长度之和,其实就是[1, n]每个数字的位数之和。
假设n = 131,则[1, 131]中,
- 位数为1的数字为
1到9,共9个数,长度之和为9; - 位数为2的数字为
10到99,共90个数,长度之和为2 × 90 = 180 - 位数为3的数字为
100到131,共32个数,长度之和为3 × 32 = 96
我们能很快计算出来所有数字的长度之和。
那么,当划分为n部分时,我们就能算出总的字符串长度,此时再用总的字符串长度,除以limit,看划分出来的是不是一共有n个部分,若是,则说明满足条件。由于题目要求n尽可能小,则我们从小开始枚举n,找到第一个符合条件的n即可。
//C++
class Solution {
public:
// 计算[1, x]所有数的位数之和
int get(int x) {
int ret = 0, i = 1;
int begin = 1, end = 10;
while (x >= end) {
ret += i * (end - begin);
i++;
begin *= 10;
end *= 10;
}
ret += (x - begin + 1) * i;
return ret;
}
// 获取x的位数
int get_bits(int x) {
int ans = 0;
while (x) ans++, x /= 10;
return ans;
}
vector<string> splitMessage(string message, int limit) {
int size = message.size();
int x = 0; // 最终划分的组数
for (int i = 1; i <= size; i++) {
int n = get_bits(i); // 位数
int tot = size + (3 + n) * i + get(i); // 总长度
int group = tot / limit;
if (tot % limit) group++;
if (group == i) {
x = i;
break;
}
}
vector<string> ans;
int pos = 0;
for (int i = 1; i <= x; i++) {
string suff = "<" + to_string(i) + "/" + to_string(x) + ">";
int len = limit - suff.size(); // 字符串中需要提供的长度
int max_len = message.size() - pos;
len = min(len, max_len);
string t = message.substr(pos, len) + suff;
ans.push_back(t);
pos += len;
}
return ans;
}
};
总结
本场比赛只做出3题,T4读题花了太久时间。
T1是双指针简单模拟;T2是动态规划;T3是图的遍历;T4是模拟。







![[UE][UE5]Gameplay框架,Actor,pawn,playerController(玩家控制器),Character(角色)之间的关系](https://img-blog.csdnimg.cn/6405a1eb7c2a4ccd898417160de69615.png)