简介

稀疏阵是在不明显改变阵列波束宽度的情况下去掉一些阵元，可以用满阵列的几分之一的阵元构造一个减低了增益的高方向性阵列，符合大型阵列设计中降低成本及软硬件复杂度的需求。
大型稀疏阵列的综合方法主要可以分为三类。第一类是确定性的稀疏化方法，通常是基于解析公式或给定模型得到确定的稀疏阵列分布。如基于差集和几乎差集的稀疏综合算法，以及参考口径幅度渐变确定分布密度的稀疏算法等。这类确定性的稀疏化算法可以根据阵列要求快速得到稀疏阵列分布形式，但是，其得到的结果一般还有较大的可优化空间。第二类是基于数值方法的快速综合方法，如矩阵束方法，迭代傅里叶方法等。这类算法具有很高的计算效率，用于对规则阵列的快速综合。另一类主要是基于智能优化算法的稀疏阵列综合，如广泛使用的遗传算法、粒子群算法等全局收敛能力较强的优化算法。这类算法将阵列中每一个阵元的激励当作一个独立变量进行优化，随机搜索的策略在阵列规模较小时具有较好的优化效果。但是，当阵列口径增大到一定规模后，解空间维数的剧增使得原来的优化策略难以在有限的时间内搜索到满意的解。

稀疏线阵

稀疏阵列天线的实现是通过在均匀阵列中按一定分布规律选取部分阵元“激活”，“关闭”（端口负载匹配）其余阵元。阵元激励为 1 时为激活状态，为 0 时即为关闭状态。其中，均匀直线阵的满阵规模为64阵元，对阵列单元关闭25%和40%进行天线阵列的稀疏，如下所示：

均匀直线阵的满阵规模为64阵元，对阵列单元关闭25%和40%进行天线阵列的稀疏的天线阵列方向图如下所示：

-15度到15度的局部放大方向图如下所示：

如上所示：稀疏阵列天线通过合理的关闭一些天线单元，可以达到降低天线副瓣，节约天线成本，同时又不明显降低天线的增益和波束宽度。

概率密度稀疏法

密度加权法是稀疏技术的一种方法，它是在满阵的基础上，按照一定的算法和法则得到稀疏阵。从统计角度上讲，稀疏阵的阵因子方向图函数在形式上与满阵的相同，通过对阵中每个单元按条件判断是否激励，对满阵方向图进行概率逼近，得到的方向图副瓣电平一般比满阵高些，单元数相对较少的阵列尤其如此，但主波束和满阵一致。由于阵元是否被激励是以对应满阵的馈电幅度分布作为概率函数来判定的，故得到的稀疏阵又称为“密度加权阵”。
稀疏阵的阵因子如下所示：

式中，F_mn称为位置函数，其取值只有两个数0和1。当F_mn=0时，处于坐标位置(x_m,y_n)的单元为 无源单元；当F_mn=1时，该位置的单元则为有源单元。F_mn的取值以样本满阵单元的归一化激励幅度I作为概率分布函数，并与一个随机数R_mn (区间[0，1]内的均匀分布的随机数)做比较来确定。如果R_mn 小于等于归一化的激励幅度I_mn，则保留该单元，否则就舍弃该单元。
相关概率密度稀疏示例如下，满阵规模为3232，稀疏率54%的稀疏阵如下所示：

满阵规模为3232，稀疏率54%的稀疏阵的方向图如下所示：

多阶密度加权法

对阵列天线口径的幅度分布进行两个或两个以上非0的台阶幅度量化，称为多阶振幅量化。这样的稀疏阵称为“多阶振幅量化阵”或“多阶密度加权阵”。把平面阵分割成N个圆环，每个圆环对应的幅度值分别为V₁，V₂…V_n,N的选择不同，就构成了不同的N阶量化。
一个二阶密度加权的稀疏示例如下，满阵规模为4040，稀疏率42%的稀疏阵如下所示：

满阵规模为4040，稀疏率42%的稀疏阵的方向图如下所示：

迭代傅里叶(IFT)综合法

均匀直线阵的阵因子如下所示：

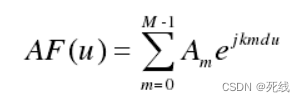
阵列激励向量{Am}与阵因子AF(u)之间满足傅里叶变换关系式。给定目标方向图AF(u)，通过快速傅里叶变换(FFT)可以计算出阵列激励{Am}。同样的，利用傅里叶逆变换(IFFT)可以根据已知阵列激励快速计算出方向图。因此，很容易利用FFT/IFFT 实现阵列方向图或阵列激励系数的迭代递推。通过不断调整目标方向图和阵列激励，通过FFT/IFFT 实现低副瓣的稀疏阵列综合。
使用迭代傅里叶算法对稀疏阵列进行综合，得到的阵列如下所示：

迭代傅里叶算法综合得到的稀疏阵列方向图如下所示：

如上所示：基础的IFT算法得到的稀疏阵列副瓣电平较差，迭代速度较快。

对称分布稀疏阵列

单脉冲雷达天线要求产生一个主瓣的和波束，以及具有两个(或四个)主瓣的差波束。要获得差方向图，一般要求激励幅度为对称分布； 激励相位为阵列左右两半相位相差 180 度。这就要求天线阵列的分布是对称的。
一个对称分布的稀疏阵列如下所示：

对称分布的稀疏阵列对应的方向图如下所示：

建模仿真

在天线仿真软件里面进行建模，其中灰色的天线表示稀疏掉的天线单元，不参与馈电，稀疏阵列模型如下所示：

稀疏阵列对应的扫描方向图如下所示：