目录
01背包理论基础
二维dp数组
1、确定dp数组以及下标的含义
2、确定递推公式
3、dp数组如何初始化
4、确定遍历顺序
5、打印dp数组
最终代码
一维dp数组
1、确定dp数组的定义
2、确定递推公式
3、初始化dp数组
4、遍历顺序
5、打印dp数组
最终代码
416. 分割等和子集
思路
分割等和子集
01背包理论基础
- 01背包问题:
- 有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大
- 01背包问题的解法:
- 暴力解法:回溯算法
- 有n个物品,其中每件物品的状态只有取和不取,使用回溯法搜索出所有的情况,所以时间复杂度为O(2^n)
- 使用回溯算法的时间复杂度是指数级别,所以需要使用动态规划的解法来进行优化
- 动态规划:
- 动态规划的解法有两种:一种是使用二维dp数组,另一种是使用一维dp数组
- 二维dp数组:dp[i][j] 表示从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少
- 一维dp数组:dp[j]表示:容量为j的背包,所背的物品价值可以最大为dp[j]
- 暴力解法:回溯算法
- 01背包问题的重要性:
- 背包问题的理论基础重中之重是01背包,一定要理解透
- 01背包和完全背包的区别是:01背包的每个物品数量只有一个,而完全背包每个物品的数量有无数个
- 还有其他的背包问题:
- 01背包:有n种物品,每种物品只有一个
- 完全背包:有n种物品,每种物品有无限个
- 多重背包:有n种物品,没有物品的个数各不相同
二维dp数组
对于动态规划的思路:一定要时刻记着5个步骤:1、确定dp数组以及下标的含义;2、确定递推公式;3、dp数组如何初始化;4、确定遍历顺序;5、打印dp数组
1、确定dp数组以及下标的含义
二维dp数组是基础,在此基础上可以优化为一维dp数组,所以要先弄清楚二维dp数组
dp[i][j]: 背包中物品的总价值
i 代表:物品遍历到物品 i
j 代表:目前背包的容量
2、确定递推公式
要求递推公式,就是要求,当前背包中的最大值该怎么获得
有两个方向:
- 由dp[i - 1][j]推出:这种情况代表,当前物品 i 放不到背包中,只能获取前 i-1 个物品放入后,所能得到的最大价值
- 由dp[i - 1][j - wight[i]]推出:这种情况代表:当前的物品 i 可以放到背包中,物品 i 的价值为 value[i] , 此时还需要知道 放了物品 i 之后,所剩容量( j - wight[i] ) 还能放的最大价值为 ( dp[i - 1][j - wight[i]] ) ,两者之和就是遍历到当前物品,容量为j的背包中可以存放的最大价值
- 当前背包的最大容量就这两种情况,所以在这两种情况中选取最大值就可以
- 最终的递推公式为:dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
3、dp数组如何初始化
初始化dp数组的时候,一定要和dp数组的定义吻合
首先,当背包容量为0时,不论遍历到哪个物品,背包中的最大价值都是0,即dp[i][0] 全为0
其次,从递推公式中可以知道,dp[i][j] 的两种状态都是由 dp[i - 1][j] 来获取的,所以 dp[0][j]的状态一定要进行初始化,因为0-1为 -1,这种情况出界了
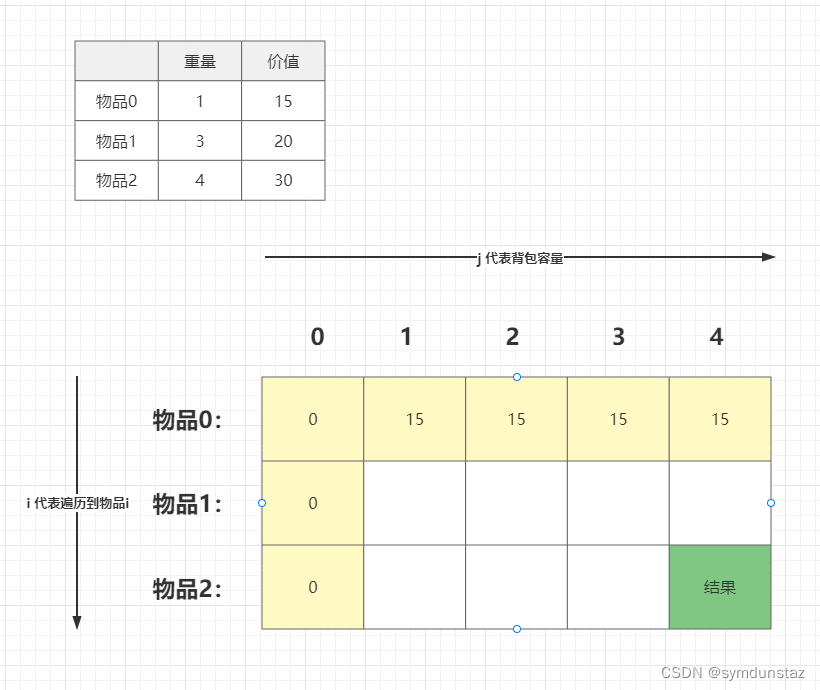
最后,是除左边界和右边界的所有情况的初始化,这些位置其实赋值任何都可以,因为在后面填充数组的过程中,其中的值还是会被 递推公式中的值所覆盖,跟本身初始化是什么值无关
4、确定遍历顺序
这里遍历右两种情况:
- 先遍历物品,再遍历背包重量
- 先遍历背包重量,再遍历物品
这两种情况都是可以的,但是先遍历物品更好理解
因为dp[i][j] 每次都是获取正上方或者左上角的数据,不会被右方的数据影响
5、打印dp数组
表格中的最后一个元素就是需要求的结果
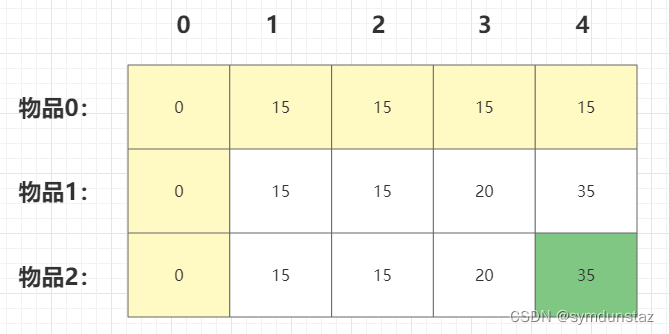
最好根据递推公式手动推导一下这个表格就很清楚了
最终代码
public class BagProblem {
public static void main(String[] args) {
int[] weight = {1,3,4};
int[] value = {15,20,30};
int bagSize = 4;
testWeightBagProblem(weight,value,bagSize);
}
/**
* 动态规划获得结果
* @param weight 物品的重量
* @param value 物品的价值
* @param bagSize 背包的容量
*/
public static void testWeightBagProblem(int[] weight, int[] value, int bagSize){
// 创建dp数组
int goods = weight.length; // 获取物品的数量
int[][] dp = new int[goods][bagSize + 1];
// 初始化dp数组
// 创建数组后,其中默认的值就是0
for (int j = weight[0]; j <= bagSize; j++) {
dp[0][j] = value[0];
}
// 填充dp数组
for (int i = 1; i < weight.length; i++) {
for (int j = 1; j <= bagSize; j++) {
if (j < weight[i]) {
/**
* 当前背包的容量都没有当前物品i大的时候,是不放物品i的
* 那么前i-1个物品能放下的最大价值就是当前情况的最大价值
*/
dp[i][j] = dp[i-1][j];
} else {
/**
* 当前背包的容量可以放下物品i
* 那么此时分两种情况:
* 1、不放物品i
* 2、放物品i
* 比较这两种情况下,哪种背包中物品的最大价值最大
*/
dp[i][j] = Math.max(dp[i-1][j] , dp[i-1][j-weight[i]] + value[i]);
}
}
}
// 打印dp数组
for (int i = 0; i < goods; i++) {
for (int j = 0; j <= bagSize; j++) {
System.out.print(dp[i][j] + "\t");
}
System.out.println("\n");
}
}
}一维dp数组
一维dp数组是对二维dp数组情况的优化,因为dp[i][j] 是在dp[i - 1][j] 的基础上得到的,所以完全可以只维护一维dp数组,可以理解成是一个滚动数组,每遍历一个物品,一维dp数组全部更新一次
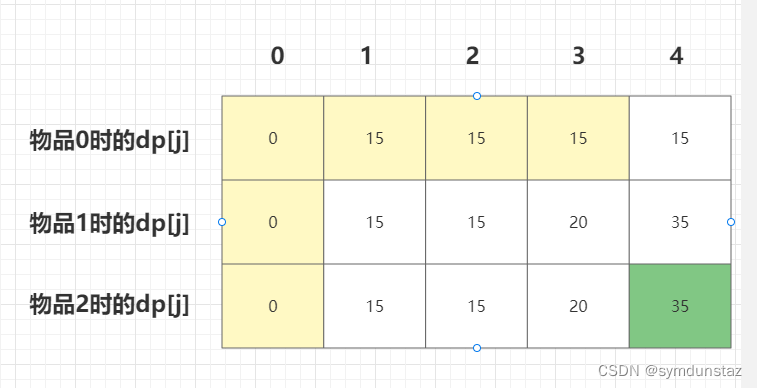
1、确定dp数组的定义
一维数组:dp[j]表示:容量为j的背包,所背的物品价值可以最大为dp[j]
2、确定递推公式
根据前面二维dp数组的递推公式来推导一下,一维dp数组的递推公式,还是两种情况:
- 由dp[j]推出,这种情况代表没有放物品 i ,所以还是原来的值,代表放入容量为 j 的前 i-1 个物品的最大价值
- 由dp[j - weight[i]],这种情况代表放了物品 i ,物品i 的价值是 value[i] , 剩余的容量(j - weigth[i])能放的 i - 1 个物品的价值为 dp[j - weight[i]],所以放物品 i 总的价值为 dp[j - weight[i]] + value[i]
- 所以 dp[j] = max(dp[j] , dp[j - weight[i]] + value[i]);
3、初始化dp数组
对于dp[0] ,也就是 背包容量为 0 的时候,肯定应该赋值为 0 ,即 dp[0] = 0
但是对于非0下标应该怎么赋值呢,其实dp数组在推导的过程中一定是取最大数的,如果题目给的价值都是正整数,那么非0下标都初始化0就可以了
这样才能让dp数组在递推公式的过程中取的最大价值,而不是被覆盖(比如初始化100 就会被覆盖)
所以假设物品的价值都是大于0的,所以dp数组初始化的时候,都初始化成0 就可以了
4、遍历顺序
这里的遍历顺序是从后向前进行遍历,因为dp[j - weight[i]]这种情况要用到上一个物品对应的数组前面的值
这种倒序遍历保证了物品 i 只被放入一次,如果从前向后遍历会造成物品被多次加入背包的情况
要清楚的是:
二维dp数组的时候是有两种写法的,一种是先遍历物品再遍历背包;另一种是先遍历背包再遍历物品,而且从前向后遍历,或者从后向前遍历都是可以的
一维dp数组是根据二维dp数组中的先遍历物品再遍历背包推导来的,而且每次获取下一个物品对应的dp[i][j]时会根据前面的dp[i-1][j-weight[i]]获得,这个数组是在当前层的左上方,所以当是一维数组的时候,移动要从后向前进行遍历,前面的数在这一层更新中还要继续使用呢
并且如果在一维数组中采用从前向后的遍历时,会导致物品被多次添加进背包,因为在确定下标大的元素的时候会用到下标小的元素,所以下标小的元素要最后才更新,所以要从后向前遍历
二维dp数组中,当前层是根据上一层来推导出来的,当前层的每一个值不受上一层的值得影响,两层得数据是完全隔离开来的,所以正序遍历和倒序遍历都可以
一维dp数组中,数组的内存空间是重复利用的,如果正序遍历,当前计算出来的值就会和旧值产生冲突
5、打印dp数组
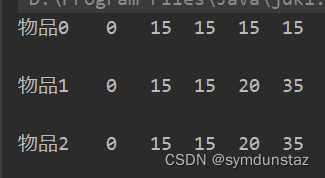
最终代码
public class BagProblem2 {
public static void main(String[] args) {
int[] weight = {1,3,4};
int[] value = {15,20,30};
int bagSize = 4;
testWeightBagProblem(weight,value,bagSize);
}
/**
* 动态规划获得结果
* @param weight 物品的重量
* @param value 物品的价值
* @param bagSize 背包的容量
*/
public static void testWeightBagProblem(int[] weight, int[] value, int bagSize){
// 创建dp数组
int[] dp = new int[bagSize + 1];
// 初始化dp数组
// 将dp[]数组初始化为0,默认就是,不用操作
// 遍历填充dp数组
// 外层循环代表几个物品,循环几次
// 内层循环更换最大值
for (int i = 0; i < weight.length; i++) {
for (int j = bagSize; j >= weight[i]; j-- ) {
dp[j] = Math.max(dp[j],dp[j-weight[i]]+value[i]);
}
// 打印dp数组
System.out.print("物品" + i + "\t");
for (int j = 0; j <= bagSize; j++) {
System.out.print(dp[j] + "\t");
}
System.out.println("\n");
}
}
}
416. 分割等和子集
题目链接:力扣
思路
这道题目是可以使用回溯法的,只要找到集合中能够出现sum/2的子集总和,那就算分割成两个相同元素和子集了
但是使用回溯法会超时,直接使用动态规划,使用背包问题解决
既然是背包问题,先要判断是什么样的背包问题,如果其中的每个物品只能使用一次,那就是01背包,如果每个物品可以使用无数次,那就是完全背包
显然这道题目是01背包
既然是01背包问题,那我们需要明确,物品、物品重量、物品价值、背包容量
物品:数组中的元素
物品重量:元素大小
物品价值:元素大小
背包容量:数组和 / 2
分割等和子集
1、确定dp[]数组的含义
使用一维dp[]数组,dp[j] 代表:当 数组和/2 为 j 时,数组中的某些元素相加可以 数组和/2
2、递推公式
两个方法可以获取:
- dp[j]
- dp[j - nums[i]] + nums[i]
所以递推公式为 dp[j] = max(dp[j],dp[j - nums[i]] + nums[i]);
3、初始化
只包含正整数,最小值为0,所以初始值默认为0
4、遍历顺序
因为这一轮数组的值是从上一轮的前方和获取的,所以需要从后向前遍历
最终代码
class Solution {
public boolean canPartition(int[] nums) {
int sum = 0;
for (int num : nums) {
sum += num;
}
if ( sum % 2 != 0) {
return false;
}
// 目标和为
int target = sum / 2;
// 创建dp[j]数组
int[] dp = new int[target + 1];
// 填充dp数组
for (int i = 0; i < nums.length; i++) {
for (int j = target; j >= nums[i]; j--) {
dp[j] = Math.max(dp[j],dp[j-nums[i]] + nums[i]);
}
}
return target == dp[target];
}
}



![[附源码]Python计算机毕业设计宠物寄养管理系统](https://img-blog.csdnimg.cn/36f3e846a56747219e1dfbf07cdf9914.png)