【数据结构】堆的拓展延伸 —— 堆排序 和 TopK问题

news2024/11/30 6:43:34

文章目录

  • 前言
  • 堆排序
  • TopK问题
  • 结语

前言

上篇博客，我们实现了堆。那么堆到底有什么应用情景？今天的内容就是堆的两个应用，堆排序和TopK问题。话不多说，我们这就开始。

堆排序

堆排序，是根据堆的结构而设计出的一种排序算法，其时间复杂度：O(N * logN)，空间复杂度：O(1)。

堆排序的前提是需要 构建一个堆，而建堆有两种方法：

向上调整建堆：

上篇博客中，我们实现过 堆的向上调整算法。我们使用向上调整方法建堆时，需要复用堆的两个接口：初始化 和 插入(插入中调用了向上调整)。

通过这种方法，我们可以建堆成功。

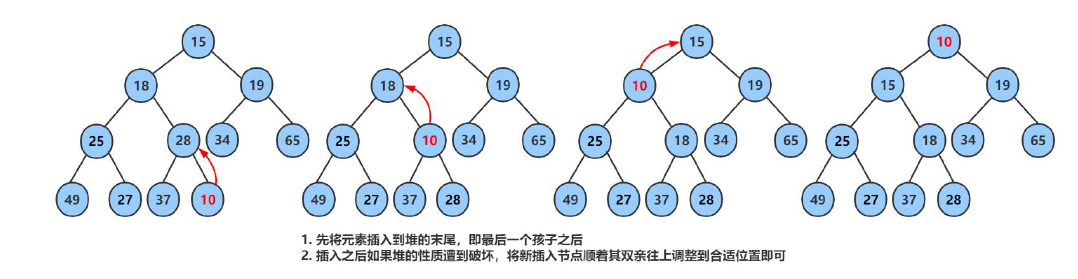
image-20221122005820778

那么它的时间复杂度怎么计算？

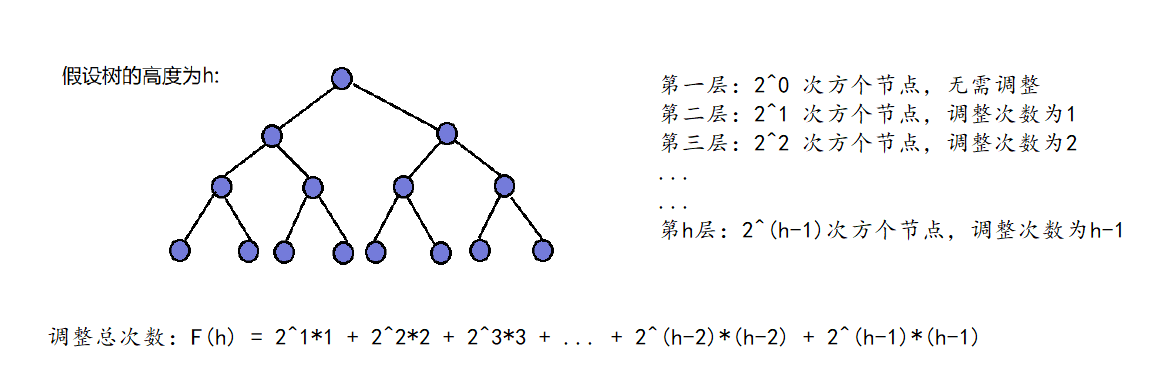
image-20221122010840677

对于 向上调整 来说，除了第一层无需调整，其他层数都需要调整。而 二叉树每层的节点是呈 2 倍递增的。

所以其实 最后一层的节点 比 前 h - 1 层 都多，最后一层的节点数为：2^(h-1) * (h-1)，再对其进行处理：2^h * (h-1)/2。

这里的 h 为 高度，我们设 N 为二叉树的总结点数。假设二叉树每一层都是满的，那么每层节点数就呈一个等比数列：20~ 2(h-1)。通过等比数列求和，可以求出二叉树的总结点数为：2^h - 1，那么就可以推导出 h 和 N 之间的关系为：2^h-1 = N.

那么式子 2^h*(h-1)/2，就可以继续转换为：(N+1)(logN-1)/2，省去常数项和除数，就可以推出 向上调整算法的时间复杂度为O(N * logN)。

那么对于向下调整呢？它的时间复杂度是否更优？

向下调整建堆：

首先明确一点，可以使用向上调整或向下调整算法的前提是，数组的结构是一个堆。向上调整算法由于是从0开始构建的，每一次push都保证它是一个堆，这点它不需要考虑。

但是对于向下调整算法来说，给定的数组可能不是一个堆，所以第一步就是将 给定数组 调成一个堆：

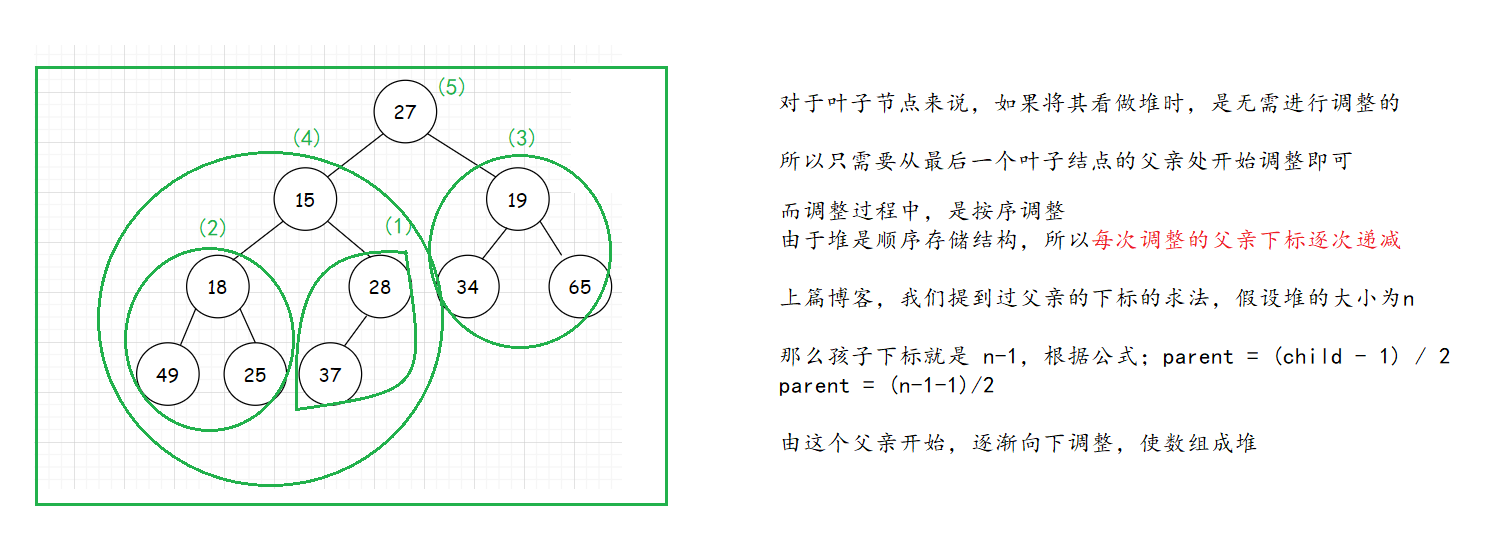
image-20221122020722056

那么建堆的时间复杂度又是多少？这里就又要进行推导：

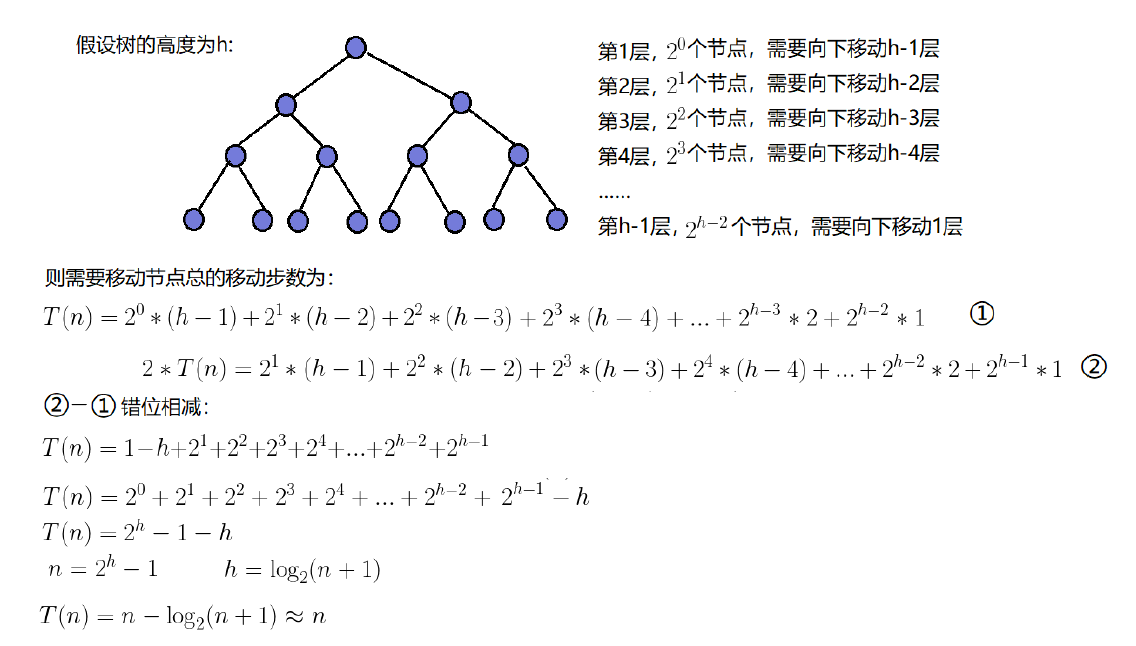
image-20221122020935978

根据推导，我们可以得知 向下调整建堆的时间复杂度为O(N)。

所以就时间复杂度上，明显向下调整建堆的方法更优。

那么接下来，就到了堆排序的第二步，选择排升序还是降序。

我们这里就举 排升序 的例子：

如果要使 堆排序的排序方式为升序，那么我们应该构建 大堆 还是 小堆 ？

先假设我们构建的是一个小堆：

image-20221122025225572

小堆被否决，我们就需要构建大堆：

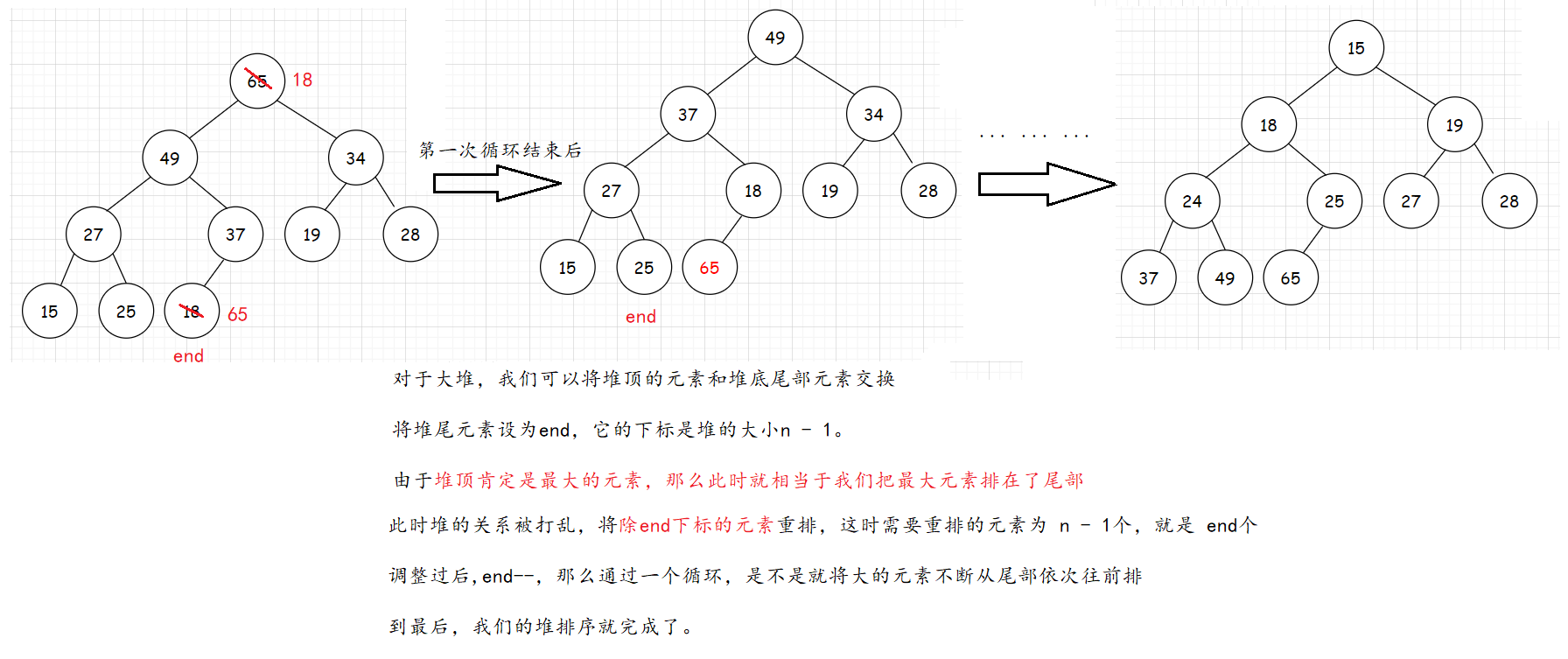
image-20221122031208122

而这里我们构建大堆在向下调整的过程中，每个节点最多向下调整 logN 次。

建堆的时间复杂度为O(N)，而排序的过程根据最后一层计算出的时间复杂度为O(N * logN)，那么整体的时间复杂度就为N+N*logN，忽略掉N，堆排序的时间复杂度为O(N * logN)

那么堆排序对比冒泡排序、插入排序等时间复杂度为O(N^2)的排序的排序速度有多快呢？

对于 N^2 的如果有100w个值，那么就要跑一万亿次；而对于 N*logN 而言，只需要跑 2000w 次。这就体现出差距了。

建大堆，排升序代码：

// 交换
void Swap(int* p1, int* p2)
{
	int tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}

// 向下调整
void AdjustDown1(int* a, int sz, int parent)
{
	int child = 2 * parent + 1;

	// 建大堆
	while (child < sz)
	{
		if (child + 1 < sz && a[child + 1] > a[child])
		{
			child++;
		}
		
		// 判断孩子是否大于父亲
		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = 2 * parent + 1;
		}
		else
		{
			break;
		}
	}
}

void HeapSort(int* a, int sz)
{
	// 建堆
	for (int i = (sz - 1 - 1) / 2; i >= 0; i--)
	{
		AdjustDown1(a, sz, i);
	}

	// 此刻堆已经建好了
	// 排升序，已经建了大堆，就需要调整元素

	int end = sz - 1;
	while (end > 0)
	{
		Swap(&a[0], &a[end]);
		AdjustDown1(a, end, 0);
		end--;
	}
}

void TestHeap1()
{
	int array[] = { 27, 15, 19, 18, 28, 34, 65, 49, 25, 37 };
	HeapSort(array, sizeof(array) / sizeof(int));

	for (int i = 0; i < sizeof(array) / sizeof(int); ++i)
	{
		printf("%d ", array[i]);
	}
	printf("\n");
}

int main()
{
	TestHeap1();
}

image-20221122144520869

TopK问题

TopK问题：即求数据结合中 前K个最大的元素或者最小的元素，一般情况下数据量都比较大。

比如 csdn的热榜前一百、世界五百强、古代的四大美女等。

对于TopK问题，能想到的最简单直接的方式就是排序，但是：如果数据量非常大，排序就不太可取了(可能数据都不能一下子全部加载到内存中)。

比如在N个数中找出最大的 k 个数。最佳的方式就是用堆来解决，而堆又有两种方案：

  1. 建立一个 N 个数的大堆，pop k 次，依次取堆顶元素，依次得到最大的 k 个数。
  2. 建立一个 k 个数的小堆，依次遍历数据，数据比堆顶数据大就替换堆顶，再向下调整堆，最后小堆中就是最大的 k 个数。

我们先分析 第一种方案：

对于 N 不大的情况，这种方法是可以的。但是如果 N 是一百亿呢，这时这些数据的大小就是40G，我们买来的电脑内存才16G，那肯定就开不了这么大的堆。

虽然它有着 k * logN 的时间复杂度，且在内存放的下的情况下，空间复杂度更是达到了O(1)，但是它因为可能有着内存放不下的风险，所以这个方案被否决了。

那么我们接着看 第二种方案：

内存中可能放不下这些数据，那么就可以放到磁盘中，也就是放到我们的文件中，有了这个前提，我们再开始。

首先，我们分析一下，为什么要建 k 个数的小堆：

我们的目的是选出 最大的 k 个数，大堆堆顶的数据为最大，如果一开始建堆的 k 个数，就包含着 N 个数中最大的数，其他的数不是最大的数之一。那么最大的数据堵在堆顶，其他数据就进不来了。所以一定要建小堆。

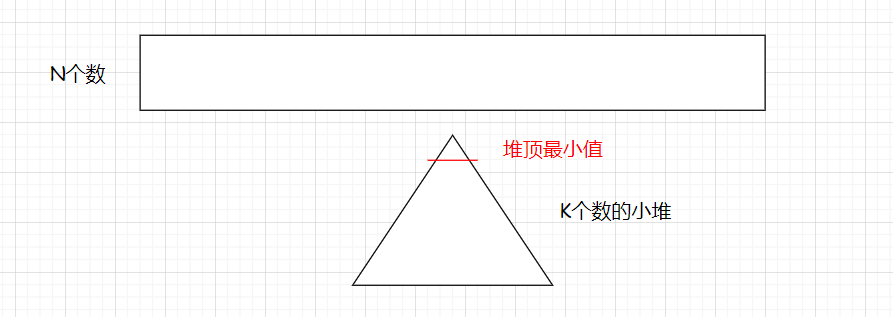
image-20221122172601196

当建好堆之后，遍历 N 个数，由于是小堆，那么遍历的数据一旦比堆顶数据大，就把元素放入堆，然后重新调整，再选出堆中最小的数，循环往复，最后堆中就是最大的 k 个数。

我们再分析一下时间复杂度，建小堆的时间复杂度为：O(k)，遍历选数的时间复杂度为：O(N - k) * logk。那么总体就是 k + (N - k) * logk，化简一下就为：O(N * logk)。

而空间复杂度由于建了 k 个数的堆，就是O(k)。

这里我们使用随机数 + 文件读写的方式，并且在文件中放入几个大于随机数最大值的数据，检测是否完成选最大的 k 个数的任务：

#define _CRT_SECURE_NO_WARNINGS 1 

#include <stdio.h>
#include <time.h>
#include <stdlib.h>
void Swap(int* p1, int* p2)
{
	int tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}

void AdjustDown2(int* a, int sz, int parent)
{
	int child = 2 * parent + 1;

	// 建小堆
	while (child < sz)
	{
		if (child + 1 < sz && a[child + 1] < a[child])
		{
			child++;
		}
		// 判断孩子是否小于父亲
		if (a[child] < a[parent])
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = 2 * parent + 1;
		}
		else
		{
			break;
		}
	}
}

void TestHeap3()
{
	int n, k;
	printf("请输入n和k:>");
	scanf("%d%d", &n, &k);
	srand((unsigned int)time(NULL));

	// 写文件
	FILE* in = fopen("data.txt", "w");
	if (in == NULL)
	{
		perror("fopen fail");
		return;
	}
	
	for (int i = 0; i <= n - 5; i++)
	{
		fprintf(in, "%d\n", rand());
	}

	// 手动输入大于随机数最大值的值
	fprintf(in, "%d\n", 66666);
	fprintf(in, "%d\n", 77777);
	fprintf(in, "%d\n", 88888);
	fprintf(in, "%d\n", 99999);
	fprintf(in, "%d\n", 55555);

	fclose(in);
	in = NULL;

	// 读文件
	FILE* out = fopen("data.txt", "r");
	if (out == NULL)
	{
		perror("fopen fail");
		return;
	}
	// 动态开辟空间
	int* minHeap = (int*)malloc(sizeof(int) * k);
	if (minHeap == NULL)
	{
		perror("malloc fail");
		return;
	}

	for (int i = 0; i < k; i++)
	{
		fscanf(out, "%d", &minHeap[i]);
	}

	int val = 0;
	// 取k个数，建小堆
	for (int i = (k - 1 - 1) / 2; i >= 0; i--)
	{
		AdjustDown2(minHeap, k, i);
	}

	// 开始调整
	while (fscanf(out, "%d", &val) != EOF)
	{
		if (val > minHeap[0])
		{
			minHeap[0] = val;
			AdjustDown2(minHeap, k, 0);
		}
	}

	// 打印minHeap 就是 topK
	for (int i = 0; i < k; i++)
	{
		printf("%d ", minHeap[i]);
	}

	printf("\n");
	fclose(out);
	out = NULL;
}

int main()
{
	TestHeap3();
}

image-20221122171628691

结语

到这里，本篇博客就到此结束了。可能看到这里，大家可能会有点迷糊。因为今天的两个应用相对于之前是有难度的，里面有很多公式的推导和证明。博主第一遍学习的时候也是迷迷糊糊的，这是正常的，多看几遍，画画图，理解一下，就会好理解很多，而博主很笨都能理解，大家这么优秀也肯定可以理解的哈哈哈。

多写多练才是最重要的！

如果觉得anduin写的还不错的话，还请一键三连！如有错误，还请指正！

我是anduin，一名C语言初学者，我们下期见！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/26267.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Sentence-BERT: Sentence Embeddings using Siamese BERT-Networks

Sentence-BERT: Sentence Embeddings using Siamese BERT-Networks

原文链接&#xff1a;https://aclanthology.org/D19-1410.pdf 概述 问题&#xff1a; BERT和RoBERT模型在进行语义匹配的时候&#xff0c;需要将每个可能的组合都输入到模型中&#xff0c;会带来大量的计算&#xff08;因为BERT模型对于句子对的输入&#xff0c;使用[SEP]来标记…
阅读更多...
C++11、17、20的内存管理-指针、智能指针和内存池从基础到实战（中）

C++11、17、20的内存管理-指针、智能指针和内存池从基础到实战（中）

C11、17、20的内存管理-指针、智能指针和内存池从基础到实战&#xff08;中&#xff09;第三章 分配器allocator和new重载1、重载operator的new和delete包括数组如果我们访问的是一个数组2、类成员操作符new重载和放置placement_newplacement new&#xff08;放置内存&#xff…
阅读更多...
并发编程（三）原子性（1）

并发编程（三）原子性（1）

【认识原子性】&#xff1a; 一个小程序认识原子性&#xff1a; package T05_YuanZiXing;import java.util.concurrent.CountDownLatch; import java.util.concurrent.locks.Lock; import java.util.concurrent.locks.ReentrantLock;public class T00_00_IPlusPlus {private …
阅读更多...
Android源码相关面试专题

Android源码相关面试专题

Android源码相关面试专题 1、Android属性动画实现原理 工作原理&#xff1a;在一定时间间隔内&#xff0c;通过不断对值进行改变&#xff0c;并不断将该值赋给对象的属性&#xff0c;从而实现该对象在该属性上的动画效果。 正在上传…重新上传取消 1&#xff09;ValueAnimato…
阅读更多...
Do Transformers Really Perform Bad for Graph Representation?

Do Transformers Really Perform Bad for Graph Representation?

Do Transformers Really Perform Bad for Graph Representation? 论文中提出了Graphormer&#xff0c;它建立在标准的Transformer架构之上&#xff0c;并且在广泛地图表示学习任务重获得了优异的成绩。同时&#xff0c;作者也提出了一些简单但是有效的结构编码方法来帮助Grap…
阅读更多...
【支付宝生态质量验收与检测技术】

【支付宝生态质量验收与检测技术】

如何验收和检测海量的支付宝生态小程序的质量&#xff0c;是一个很重要的课题。本次分享会简单介绍如何通过平台化的方式在小程序入驻环节进行准入验收&#xff0c;以及使用前端自动化测试技术和智能化算法对小程序质量进行检测。希望能对小程序质量的验收和测试提供参考。讲师…
阅读更多...
计算机网络-应用层（应用层概述，网络应用模型（C/S模型，P2P模型），DNS域名协议）

计算机网络-应用层（应用层概述，网络应用模型（C/S模型，P2P模型），DNS域名协议）

文章目录1. 应用层概述2. 网络应用模型3. 域名系统&#xff08;DNS&#xff09;1. 应用层概述 应用层概述&#xff1a;应用层对应用程序的通信提供服务。 应用层协议定义&#xff1a; 应用进程交换的报文类型&#xff0c;请求还是响应各种报文类型的语法&#xff0c;如报文中…
阅读更多...
分布式锁-简单入门

分布式锁-简单入门

状态不是很好&#xff0c;记一下以前学过的分布式锁吧。 样例简介 不谈大概念&#xff0c;就是简单入门以及使用。 为什么要用分布式锁呢&#xff1f; 假设我需要一个定时操作&#xff0c;每天在某个点&#xff0c;我要处理一批数据&#xff0c;要先从数据库中查询出来&…
阅读更多...
云计算-Hadoop-2.7.7 最小化集群的搭建（3台）

云计算-Hadoop-2.7.7 最小化集群的搭建（3台）

云计算-Hadoop-2.7.7 最小化集群的搭建&#xff08;3台&#xff09; 文章目录云计算-Hadoop-2.7.7 最小化集群的搭建&#xff08;3台&#xff09;一、环境依赖下载二、部署概要三、hadoop101模板机配置1. 更新 & 升级2. 安装好用的vim VimForCpp3. 安装必要依赖4. 关闭防火…
阅读更多...
nginx配置https访问 生成ssl自签名证书，浏览器直接访问

nginx配置https访问 生成ssl自签名证书，浏览器直接访问

问题 nginx配置自签名ssl证书&#xff0c;来支持https访问nginx&#xff0c;在浏览器中访问nginx时&#xff0c;提示有风险。而访问其他各大网站时&#xff0c;也是使用了https协议&#xff0c;为什么可以直接访问&#xff0c;而不提示有风险呢&#xff1f; 解疑 先从ssl证书…
阅读更多...
MyBatis--动态SQL

MyBatis--动态SQL

Emp类 1.if标签 通过test属性中的表达式判断标签中的内容是否有效 (是否会拼接到SQL中) 接口 映射 测试 2.Where标签 where标签的三个作用 若where标签中有条件成立 , 会自动生成where关键字会自动将where标签中内容前多余的and去掉 , 但是其中内容后多余的and无法去掉若where标…
阅读更多...
mysql explain和DESC性能分析

mysql explain和DESC性能分析

mysql explain和DESC 根据执行时间去只可以粗略的判断sql的性能&#xff0c;我们如果想去查看一条sql语句的性能还需要explain去查看sql的执行计划。 EXPLAIN 或者 DESC 命令获取 MySQL 如何执行 SELECT 语句的信息&#xff0c;包括在 SELECT 语句执行过程中表如何连接和连接的…
阅读更多...
如何做好供应商绩效管理？

如何做好供应商绩效管理？

供应商绩效管理是一种商业行为&#xff0c;用于衡量、分析和管理供应商的绩效。供应商管理专业人员寻求削减成本&#xff0c;减轻风险并推动持续改进。企业可使用供应商管理系统来监测供应商的绩效水平。 供应商绩效管理最佳实践 所有企业都必须发展核心竞争力&#xff0c;有…
阅读更多...
【Linux 网络编程 】

【Linux 网络编程 】

Linux 网络编程背景知识&#xff1a;主机字节序列和网络字节序列IP地址的转换API网络编程接口网络节序与主机节序转换函数IP地址转换函数数据读写TCP编程编程步骤&#xff1a;客户端链接服务端成功的条件多线程实现服务端并发多进程实现服务端并发注意&#xff1a;UDP编程编程步…
阅读更多...
自动化测试基础简介（本质）

自动化测试基础简介（本质）

目录 前言 1.自动化基础 2.分层的自动化测试 2.1 单元自动化测试 2.2 接口自动化测试 2.3 UI自动化测试 3.适合自动化的项目 4.自动化测试模型 4.1线性测试 4.2模块化与类库 4.3数据驱动测试 4.4关键字驱动测试 5.POM设计模式 总结 前言 随着软件系统规模的日益…
阅读更多...
应对Redis缓存污染问题，你应该知道这些内容

应对Redis缓存污染问题，你应该知道这些内容

前言 我们在使用Redis做为缓存时&#xff0c;能加速我们对于热点数据的查询。但是如果缓存中有大量的数据不再热门了&#xff0c;从而占据着大量的内存空间&#xff0c;那么我们的Redis性能就会收到很大影响。该如何解决这个问题呢&#xff1f;本文给你答案。 什么是缓存污染…
阅读更多...
kafka开发环境搭建

kafka开发环境搭建

1 kafka开发环境 1.1 安装Java环境 1.1.1 下载linux下的安装包 登陆网址https://www.oracle.com/technetwork/java/javase/downloads/jdk8-downloads-2133151.html 下载完成后&#xff0c;Linux默认下载位置在当前目录下的Download或下载文件夹下&#xff0c;通过命令cd ~/…
阅读更多...
轻松学习string类常用接口(附模拟实现)

轻松学习string类常用接口(附模拟实现)

目录 String的常用接口说明(最常用的) string类对象的容量操作 string类对象的访问及遍历操作 string类对象的修改操作 string类非成员函数 深浅拷贝 简介&#xff1a;Cstring 是C中的字符串。 字符串对象是一种特殊类型的容器&#xff0c;专门设计来操作的字符序列。 不像…
阅读更多...
MySQL 全文检索的实现

MySQL 全文检索的实现

微信搜「古时的风筝」&#xff0c;还有更多技术干货 这有朋友聊到他们的系统中要接入全文检索&#xff0c;这让我想起了很久以前为一个很古老的项目添加搜索功能的事儿。 一提到全文检索&#xff0c;我们首先就会想到搜索引擎。也就是用一个词、一段文本搜索出匹配的内容。一般…
阅读更多...
Vue3中的组合Api与响应函数

Vue3中的组合Api与响应函数

文章目录1. 组合Api介绍setup2. 响应函数2.1 ref2.2 reactive2.3 toRef和toRefs2.4 readonly2.5 customRef1. 组合Api介绍 组合Api其实时用于解决功能、数据和业务逻辑分散的问题&#xff0c;使项目更益于模块化开发以及后期维护。 vue2.x — optionsApi 配置式Api — react类…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023