本片文章主要讲述domain中复杂业务需求的逻辑构思,关于doamin的使用位置会在另一篇文章中体现。
·二叉树与波兰式
在讲述domain的使用前先讲解一下科班生必学的《数据结构与算法》中二叉树遍历与波兰式的内容,如果你会二叉树先序遍历与波兰式转换请直接跳到下一节。
二叉树:二叉树(Binary tree)是树形结构的一个重要类型,许多实际问题抽象出来的数据结构往往是二叉树形式,其下面展示的就是某个二叉树的结构。

树的相关基本术语:
上面展示的二叉树中,有一个根节点(F)
然后有它的左子树(cadb)和右子树(ehgm)
左子树(cadb)的子树根节点(B)是二叉树根节点(F)的子节点
在数据结构中,树有三种遍历方式:
- 先序遍历
- 中序遍历
- 后序遍历
先序遍历:即为 根左右 结构遍历,按上方展示二叉树遍历顺序为(FCADBEHGM)
中序遍历:即为 左根右 结构遍历,遍历顺序为(ACBDFHEMG)
后序遍历:即为 左右根 结构遍历,遍历顺序为(ABDCHMGEF)
为了方便记忆,可以用根的先后顺序来对应记忆,先访问根节点的就是先序遍历
·中缀表达式、波兰式与逆波兰式
中缀表达式
一般我们上小学时所使用的数学计算公式就是中缀表达式,即2*(1+3)的形式
把它转换成二叉树的模样就是这个样子
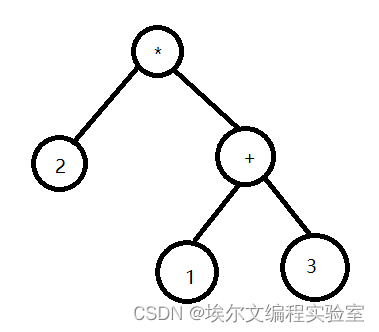
中缀表达式有助于我们对二叉树的构造与理解,可对于计算机来说,这将是复杂的且难以理解的。
所以,波兰数理科学家提出了两个适用于计算机的遍历表达式,为了纪念他们的贡献,则将其命名为波兰表达式和逆波兰表达式
波兰表达式和逆波兰表达式的数理与先序遍历和后序遍历的遍历思想一致
波兰表达式则是对二叉树先序遍历的具象表达,则是先访问根节点,再访问左子节点,最后访问右子节点,遍历后的结果是*2+13
逆波兰表达式则是对二叉树的后序遍历的具象表达,即为先访问左子节点,再访问右子节点,最后才访问根节点,遍历后的结果是213+*
·中缀表达式与波兰式的转换
在odoo的domain中,对应业务中的复杂的逻辑,我们去直接画二叉树再去遍历访问写出波兰式则是一种时间的浪费,其实可以对中缀表达式直接转换为波兰式
还是以案例2*(1+3)来解析,在真实业务中每一个数字代表一个筛选条件例如:(‘state','=','pending'),而运算符则代表逻辑符例如:'|',所以在下面的解析中,会将数字称为业务节点,运输符称为逻辑节点。至于domain中可能会出现的逻辑符号以及对应的级别会以表展示,此处先解析思想。
先序遍历:先将业务节点与逻辑节点用括号隔开 (2)*((1)+(3)),然后将逻辑节点前移一个级,与业务节点同级的逻辑节点前移到最左 *(2)+((1)(3)),然后将括号全部打开得到结结果 *2+13
后序遍历也一样:(2)*((1)+(3)) >>> (2)((1)(3)+)* >>> 213+*
·odoo中的domain
对于odoo中domain的写法[('a','=','b')]也恰好更适合使用波兰式
在domain中简单的单调与逻辑是默认使用的,例如:我希望想要state为draft和pending且active为真的
[('state','in',('draft','pending')),('active','=',True)]但对于复杂逻辑就需要用到波兰式了
例如:我希望有department_id为2且state为draft的或state为pending且send_id为5的数据
按中缀表达式表达则为((department_id=2)&(state=draft))|((state=pending)&(send_id=5))
写进domain则为
['|','&',('department_id','=',2),('state','=','draft'),'&',('state','=','pending'),('send_id','=',5)]