链接：https://www.cs.usfca.edu/~galles/visualization/Algorithms.html

可以点击 Indexing 下的 B Trees 和 B+ Trees 去学习。

为什么需要B树

对 B 树的需求随着访问物理存储介质（如硬盘）的时间减少而增加。辅助存储设备速度较慢，容量较大。需要这种类型的数据结构来最大限度地减少磁盘访问。

其他数据结构如二叉搜索树、avl 树、红黑树等只能在一个节点中存储一个键。如果必须存储大量键，则此类树的高度将变得非常大，并且访问时间也会增加。

但是，B 树可以在单个节点中存储许多键，并且可以有多个子节点。这大大降低了高度，允许更快的磁盘访问。

B- 树和 B 树都指的都是 B 树，此外还有 B+ 树。

B 树的特点

可以把 B 树理解为一个有序的多叉树。

满足下列要求的 m 阶树：

（1）每个节点最多拥有 m 个孩子结点（即至多有 m-1 个关键字）

（2）每个结点的结构为

第一个位置的 n 用来表示结点有多少个关键字。
Pn 表示子树的指针，顺着指针可以找到子树的位置。
k 表示关键字。

例如：m = 4 的 4 阶 B 树

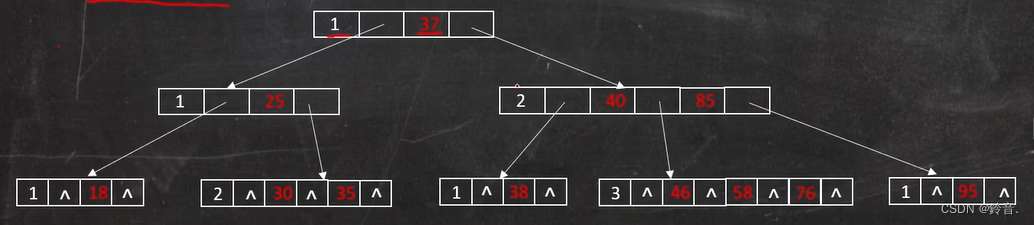
（3）除根节点外，其他结点至少有 m / 2 （向上取整）个孩子结点。

（4）若根节点不是叶子结点，则根节点至少有两个孩子结点。

（5）所有叶子结点都在同一层上，即B树是所有结点的平衡因子均等于0的多路查找树。

（6）除根节点外，其他节点都包含 n 个 key ，其中 [m/2]-1<=n<=m-1。

B树的查找

已知一棵三阶 B 树如下图所示，给出在 B 树中查找 37 的过程。

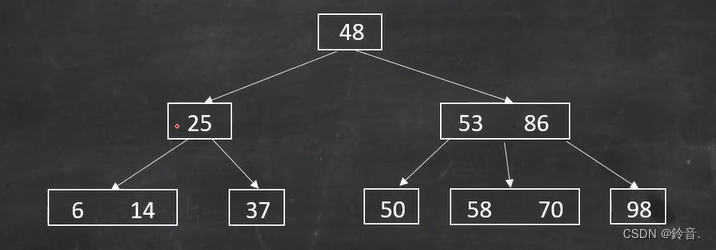
查找37，根节点是48，48>37，看48的左子树，25<37，看25的右子树，37=37。

那具体是怎么查找的呢？？

首先来了解一下操作系统的磁盘预读。

磁盘预读：

• 内存跟磁盘发生数据交互的时候，一般情况下有一个最小的逻辑单元，称之为页，datapage。
• 页一般由操作系统决定是多大，一般是4k或者16k，我们在数据交互时，可以取页的整数倍来进行读取。

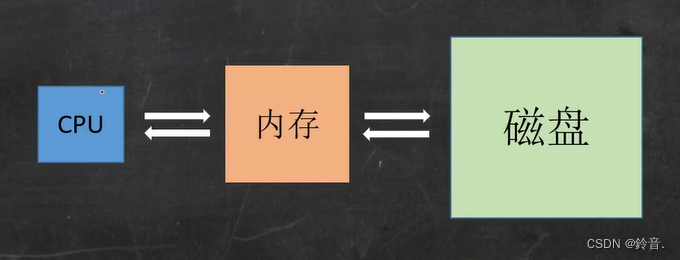
CPU要先把数据加载到内存中然后磁盘从内存中读取数据。

比如说这个 word 文档右击查看它的属性，虽然大小是46.9KB，但是占用空间是48KB，这是4K的整数倍，也就是磁盘加载数据到内存中都是datapage的整数倍。

我们可以结合操作系统知识理解 B 树的查找过程。

键值：表中的主键
指针：存储子节点的信息
数据：表记录中除主键外的数据

B树的每一个结点都是放在磁盘块里的，且一般规定磁盘块大小是16K

假如要在图中找一个关键字为28的数据：

首先把磁盘上的这个块加载到内存里，16<28，34>28，找到磁盘块1的p2，这是进行的第一次IO。

然后顺着磁盘块1的p2找到磁盘块3，再把磁盘块3加载到内存里面，然后28<25，28>31，找到磁盘块3的p2了。这是第二次IO。

然后顺着磁盘块3的p2找到磁盘块8，再把磁盘块8加载到内存里，28=28，返回关键字28对应的data。这是第三次IO。

B+树的引入

现在这个B树总共有三层，每个结点 datapage 是 16k ，假设指针和关键字不占用 datapage (占用很小)，每个 data 占用 1k ，所以三层 B 树可以存储的 data 个数是16*16*16=2^12=4096条，还是在不考虑指针和关键字的 datapage 情况下的。所以如果要是存 10000 条数据的时候怎么办呢？或许你想到的是再给 B 树加一层，确实可以这样存储 10000 条数据，但是这样的话层数增多了，查找数据就要再多一次 IO 操作，再多一次 IO 操作那查找的速度不就又慢了吗？

那为什么 B 树要存储更多数据只能增加层数呢？因为存储空间都用来放 data 了，如果只存指针和关键字的话所占用的磁盘空间是非常小的，所以我们可以把 data 都放在叶子结点上，非叶子结点只存指针和关键字，可以提升查找速度，这就是 B+ 树。

B+ 树结构长这样：

datapage 还是 16k ，假设每对指针和关键字（例如 上图磁盘块1的p1 ，28 ）只占 10 个字节，那么一个结点可以存16000/10=1600个数据，三层结构可以存储 1600*1600*1600 千万级数据，存储的数据是非常多的。

B树的删除

已知一棵 5 阶（度）B 树如下图所示，给出在B树中删除 80、200、180、50、140 的过程。

要将删除非叶子节点的关键字转换为删除叶子节点关键字。在 B 树性质里，m阶树，除根节点外，其他节点都包含 n 个 key ，其中 [m/2]-1<=n<=m-1

如果节点删除一个关键字后，节点关键字依然大于 [m/2]-1个，那么不需要去做任何的变动直接删除就可以；如果删除关键字后小于 [m/2]-1个key，那么就需要让下一个节点的关键字补上来

在 B 树中删除 80、200、180、50、140 的过程如下：

• 删除 80 ：删除 80 后，节点关键字依然大于等于 2 个，那么不需要去做任何的变动直接删除就可以。
• 删除 200 ：删除 200 后节点关键字是 1 个，所以如果要删除 200 ，那么就要先找到 200 的下一个关键字，230，让 230 代替 200 ，然后再删掉 230 。
  
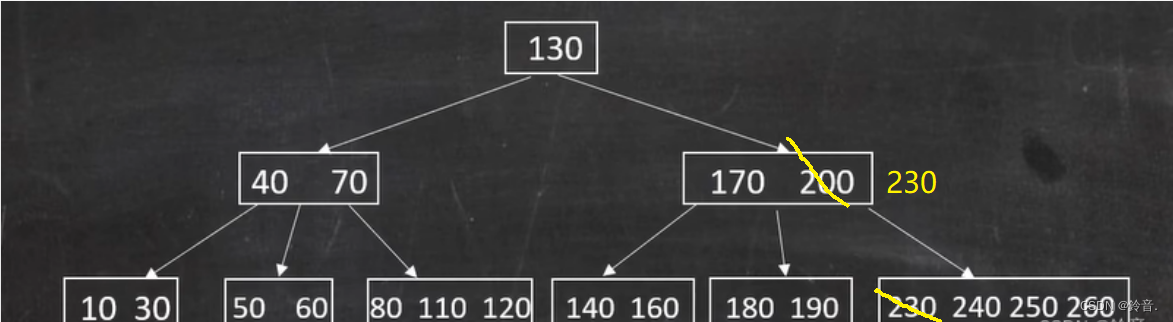
• 删除180：如果删除的是 180（此时已经删除 200 ），此节点只有一个关键字不满足节点关键字 >= 2 。
  
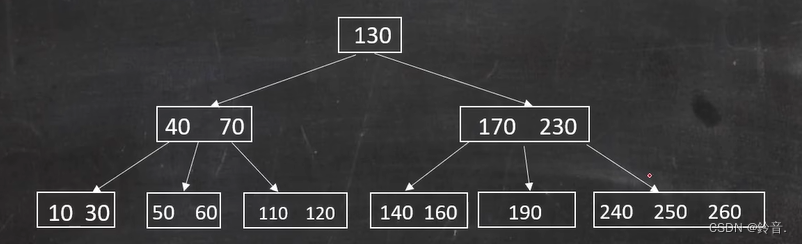
  那么需要让父节点 230 代替 180 ，再让子节点 240 补上原来 230 的位置，才能仍满足每个节点关键字 >= 2 ，结果如下：
  
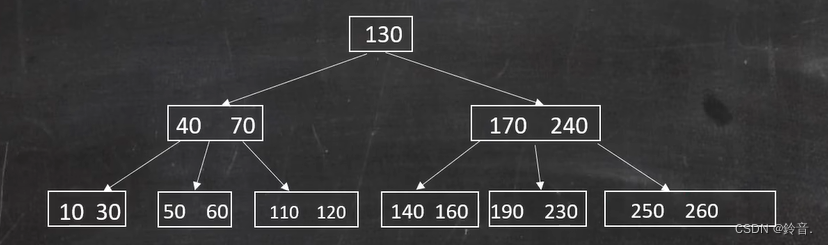
• 删除 50 ：删除 50 后该节点关键字个数为 1 ，需要再加 1 个关键字才能满足B树性质，但是它的兄弟节点都是 2 个关键字，没法再给它一个关键字了，所以这个时候就需要找父节点要一个关键字（兄弟没有钱时找爸爸要）。
  
  那么此时就先把父节点拉下来一个关键字。
  
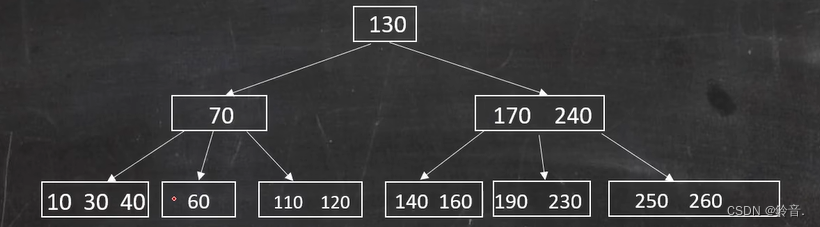
  然后再把兄弟节点合并了。
  
  此时父节点不够两个关键字，那么需要找父节点的兄弟节点要一个关键字，如果父节点的兄弟节点没有关键字，那么就找父节点的父节点的父节点要一个关键字（爸爸找兄弟借，兄弟也没有那就找爷爷借），所以只能降低树的高度，变成了下面这样。
  
  然后发现没有根节点，所以把兄弟节点进行合并，变成一个正常的 B 树。
  
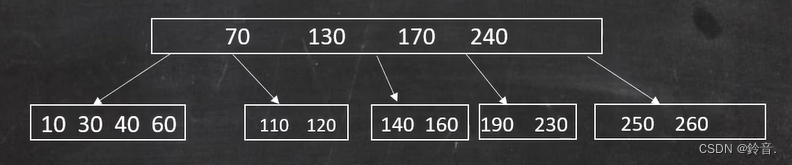
• 删除 140 ：删除 140 后，变成了这样。
  
  然后从父节点拿一个关键字，变成了这样。
  
  为了维持 B 树的特点再和兄弟节点进行合并，最终结果就是这样。