纸牌博弈问题

作者：Grey

原文地址：

博客园：纸牌博弈问题

CSDN：纸牌博弈问题

题目描述

有一个整型数组 A，代表数值不同的纸牌排成一条线。玩家 a 和玩家 b 依次拿走每张纸牌，
规定玩家 a 先拿，玩家 b 后拿，
但是每个玩家每次只能拿走最左或最右的纸牌，
玩家 a 和玩家 b 都绝顶聪明，他们总会采用最优策略。
请返回最后获胜者的分数。

注：给定纸牌序列 A 及序列的大小 n，请返回最后分数较高者得分数(相同则返回任意一个分数)。保证 A 中的元素均小于等于1000。且 A 的大小小于等于300。

题目链接：牛客-纸牌博弈

暴力递归解

定义两个递归函数，第一个递归函数是

int first(int[] A, int n, int start, int end)

这个递归函数表示的含义是：先手在数组 A 的 start 到 end 范围内，经过 n 轮，能获得的最大的分数是多少。

base case 是，当 start == end 的时候，即数组 A 只有一个元素，此时先手直接拿走这个元素，最大分数就是此时先手拿走的唯一元素值，即

        if (start == end) {
            return A[start];
        }

第二个递归函数是

int second(int[] A, int n, int start, int end)

这个递归函数表示的含义是：后手在数组 A 的 start 到 end 范围内，经过 n 轮，能获得的最大的分数是多少。

base case 是，当 start == end 的时候，即数组 A 只有一个元素，此时这个元素肯定要被先手拿走，那么后手只能返回 0，即

        if (start == end) {
            return 0;
        }

接下来是普遍情况，对于先手函数来说，有两个位置可以选，一个是 start 位置，另外一个是 end 位置，如果选了 start 位置，那么先手在下一轮就是后手，即

A[start] + second(A, n, start + 1, end)

同理，如果选 end 位置，先手在下一轮是后手，即

A[end] + second(A, n, start, end - 1)

先手函数在做上述两个决策的过程中，一定要取最大值，即

Math.max(A[start] + second(A, n, start + 1, end), A[end] + second(A, n, start, end - 1));

所以，先手函数的完整代码如下

    public static int first(int[] A, int n, int start, int end) {
        if (start == end) {
            return A[start];
        }
        return Math.max(A[start] + second(A, n, start + 1, end), A[end] + second(A, n, start, end - 1));
    }

接下来是后手函数的普遍情况，对于后手函数来说，没有先选的权力，只能让先手选完自己才能选，先手如果选了 start 位置，后手面对的选择是

first(A, n, start + 1, end)

先手如果选了 end 位置，后手面对的选择就是

first(A, n, start, end - 1)

后手在下一轮就是先手，所以要保证先手的上述选择最小，即

Math.min(first(A, n, start + 1, end), first(A, n, start, end - 1));

定义了先手函数和后手函数，主函数做如下调用即可

    public static int cardGame(int[] A, int n) {
        // 没有元素，直接返回0分
        if (n == 0) {
            return 0;
        }
        // 只有一个元素，无论如何，只能得到 A[0] 分
        if (n == 1) {
            return A[0];
        }
        // 只有两个元素，选最大的那个
        if (n == 2) {
            return Math.max(A[0], A[1]);
        }
        // 普遍情况：先手后手中最大的那个
        return Math.max(first(A, n, 0, A.length - 1), second(A, n, 0, A.length - 1));
    }

超时

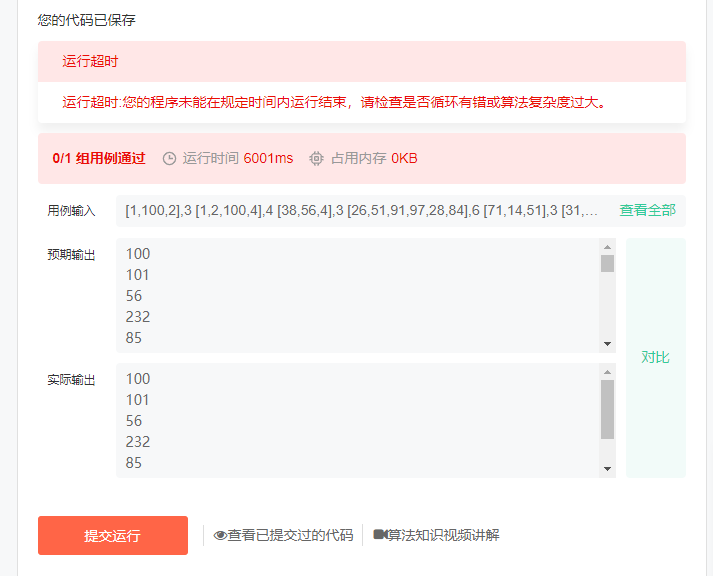
动态规划解

根据上述暴力递归函数可知，两个递归函数都可变参数都是 2 个，且可变参数的变化范围是固定的，所以我们可以用两个二维数组来分别表示两个递归函数的结果，

// 保存先手函数的递归过程解
int[][] firstMap = new int[n][n];
// 保存后手函数的递归过程解
int[][] secondMap = new int[n][n];

由于递归过程的两个可变参数 start 和 end 是有范围的，且 start 不可能大于 end，所以，上述两个二维数组的左下半区都是无效区域，无需考虑。

在暴力递归过程中，当 start == end 的时候，返回 A[start] 值，所以，针对 firstMap，其对角线（start == end）的值都是确定的

        // 对角线
        for (int i = 0; i < n; i++) {
            firstMap[i][i] = A[i];
        }

经过上述过程，可以得到两个二维数组的如下区域的内容

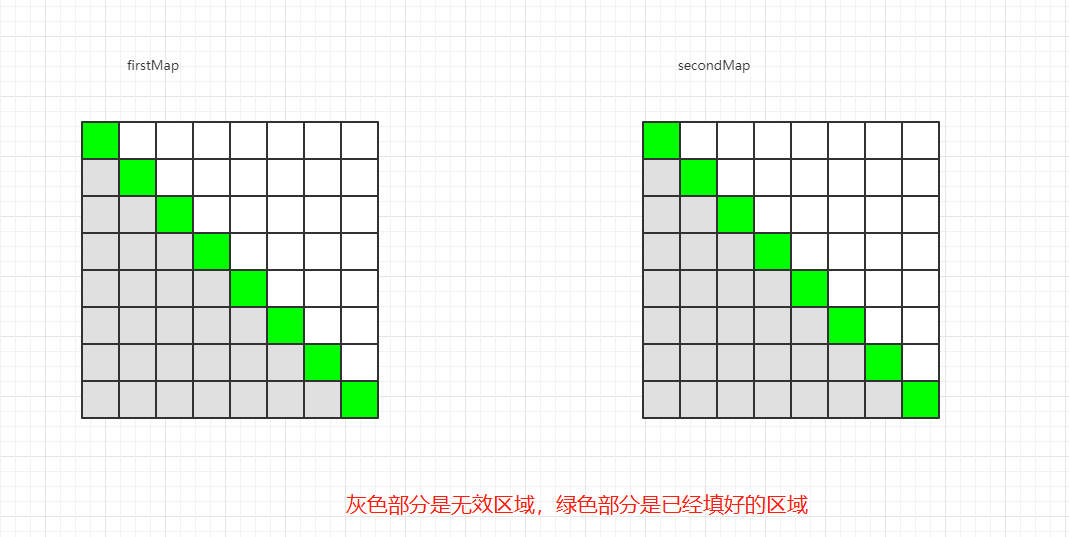
接下来就是普遍情况，

基于暴力递归过程可以很方便得到两个二维数组之间的递推关系

        // 对角线下班区域不用管
        // 对角线上半区域
        for (int i = 1; i < n; i++) {
            int r = 0;
            int c = i;
            while (c < n) {
                firstMap[r][c] = Math.max(A[r] + secondMap[r + 1][c], A[c] + secondMap[r][c - 1]);
                secondMap[r][c] = Math.min(firstMap[r + 1][c], firstMap[r][c - 1]);
                r++;
                c++;
            }
        }

完整代码如下

import java.util.*;

public class Cards {

    public static int cardGame(int[] A, int n) {
        if (n == 0) {
            return 0;
        }
        if (n == 1) {
            return A[0];
        }
        if (n == 2) {
            return Math.max(A[0], A[1]);
        }
        int[][] firstMap = new int[n][n];
        int[][] secondMap = new int[n][n];
        // 对角线
        for (int i = 0; i < n; i++) {
            firstMap[i][i] = A[i];
        }
        // 对角线下班区域不用管
        // 对角线上半区域
        for (int i = 1; i < n; i++) {
            int r = 0;
            int c = i;
            while (c < n) {
                firstMap[r][c] = Math.max(A[r] + secondMap[r + 1][c], A[c] + secondMap[r][c - 1]);
                secondMap[r][c] = Math.min(firstMap[r + 1][c], firstMap[r][c - 1]);
                r++;
                c++;
            }
        }
        return Math.max(firstMap[0][n - 1], secondMap[0][n - 1]);
    }
}