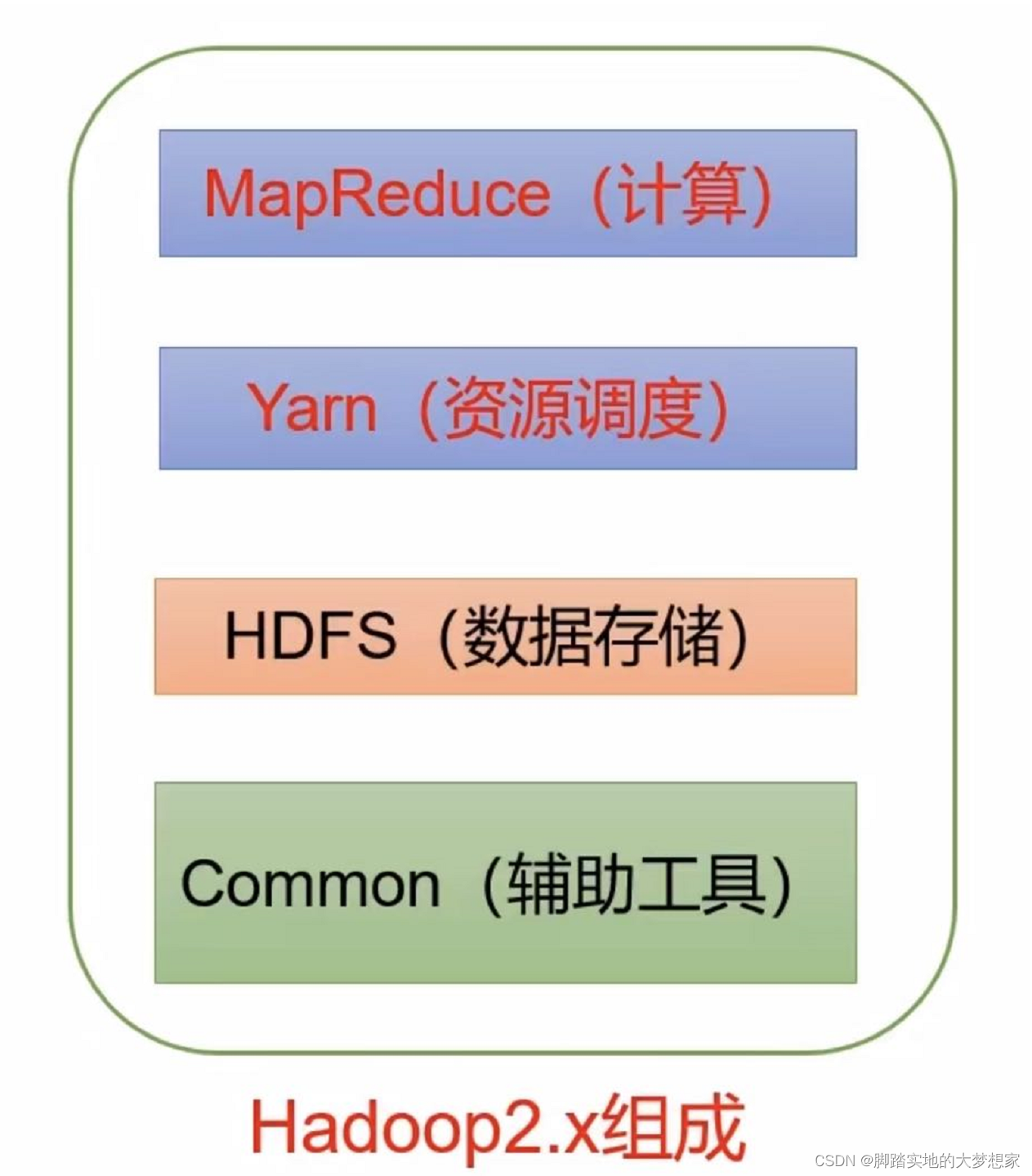
使用Python的马尔科夫链实例的实践 一行行的代码解密马尔可夫链。
当我开始学习物理时,我并不喜欢概率的概念。我对用物理学可以对整个世界进行建模的想法非常振奋,不确定性的想法让我很生气:)
事实是,当我们想研究真实的现象时,我们迟早都必须处理一定程度的不确定性。而处理它的唯一方法是获得对支配我们过程的概率的准确估计。
马尔科夫链是一个很好的方法。马尔科夫链背后的想法是非常简单的。
未来将发生的一切只取决于现在正在发生的事情。
用数学术语来说,我们说有一个随机变量X_0, X_1, ..., X_n的序列,可以在某个集合A中取值。然后我们说,如果一个事件的序列是一个马尔科夫链,我们就有。
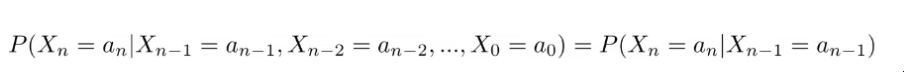
图片由我用LaTeX生成 如何用python生成LaTex请参考链接:
这听起来很复杂,但它只不过是上面所表达的概念而已。
另一个假设是,该方程对每一步都有效(不仅是最后一步),而且概率总是相同的(尽管从形式上看,这只对同质马尔科夫链而言是真的)。
现在,可能状态A的集合通常被表示为样本空间S,你可以用所谓的过渡概率来描述从S中的一个状态x到S中的一个状态y的概率。
但我答应过你,这将是一篇 "手把手 "的文章,所以让我们开始把这些概念形象化吧!
公平地说,Python不是进行数值模拟的最佳环境。专业研究人员使用的是更复杂的、在某些方面更可靠的语言,如C或Fortran。
尽管如此,本博客的目标是介绍一些非常简单的概念,使用Python可以使这个学习过程更容易。
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
plt.style.use('ggplot')
plt.rcParams['font.family'] = 'sans-serif'
plt.rcParams['font.serif'] = 'Ubuntu'
plt.rcParams['font.monospace'] = 'Ubuntu Mono'
plt.rcParams['font.size'] = 14
plt.rcParams['axes.labelsize'] = 12
plt.rcParams['axes.labelweight'] = 'bold'
plt.rcParams['axes.titlesize'] = 12
plt.rcParams['xtick.labelsize'] = 12
plt.rcParams['ytick.labelsize'] = 12
plt.rcParams['legend.fontsize'] = 12
plt.rcParams['figure.titlesize'] = 12
plt.rcParams['image.cmap'] = 'jet'
plt.rcParams['image.interpolation'] = 'none'
plt.rcParams['figure.figsize'] = (12, 10)
plt.rcParams['axes.grid']=False
plt.rcParams['lines.linewidth'] = 2
plt.rcParams['lines.markersize'] = 8
colors = ['xkcd:pale orange', 'xkcd:sea blue', 'xkcd:pale red', 'xkcd:sage green', 'xkcd:terra cotta', 'xkcd:dull purple', 'xkcd:teal', 'xkcd: goldenrod', 'xkcd:cadet blue',
'xkcd:scarlet']
因此,让我们深入了解一下:这是你需要的东西是一堆主流的库,如pandas、matplotlib、seaborn和numpy。
让我们从最简单的场景开始。
-
随机漫步
简单随机漫步是一个极其简单的随机漫步的例子。
第一个状态是0,然后你以0.5的概率从0跳到1,以0.5的概率从0跳到-1。
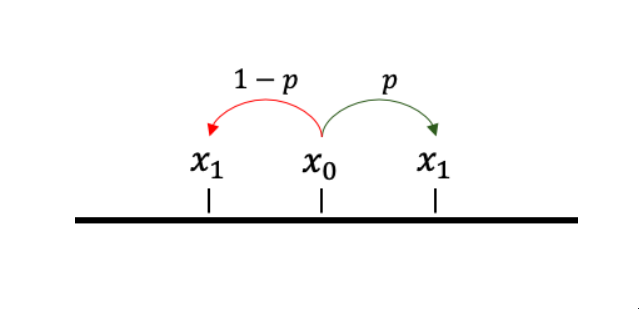
图片由我使用Power Point制作
然后你对x_1, x_2, ..., x_n做同样的事情。
你认为S_n是时间n的状态。
有可能证明(实际上非常容易),在时间t+1时处于某种状态的概率,即一个整数x,只取决于时间t的状态。
因此,这就是如何生成它。
start = 0
x = []
n = 10000
for i in range(n):
step = np.random.choice([-1,1],p=[0.5,0.5])
start = start + step
x.append(start)
plt.plot(x)
plt.xlabel('Steps',fontsize=20)
plt.ylabel(r'$S_{n}$',fontsize=20)
而这就是结果:
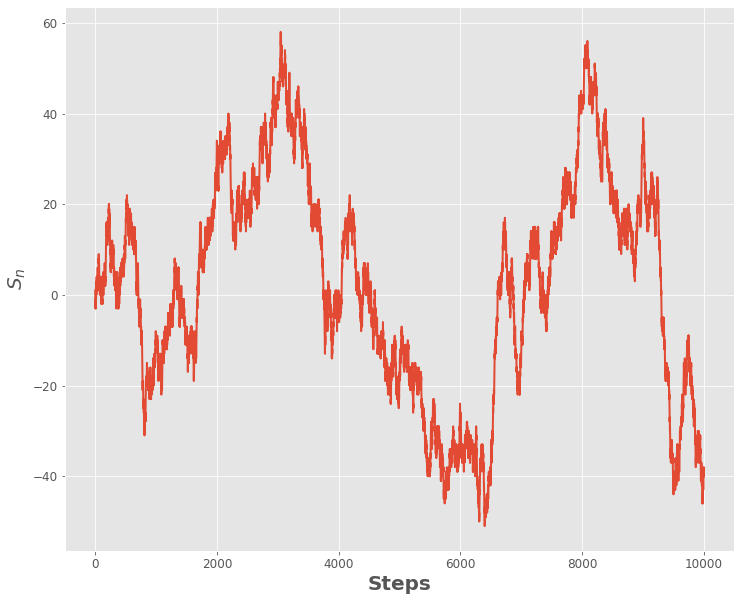
现在,随机漫步的想法是模拟如果我们决定从一个点开始,通过投掷一枚完美的硬币随机选择向上或向下,将会发生什么。
这个过程相当简单,但就其理论应用和特性而言,却非常有趣。
这个过程的第一个合理的扩展是考虑一个随机行走,但有一个非完美的硬币。这意味着,上升的概率与下降的概率不一样。这被称为有偏见的随机漫步。
让我们考虑以下几个概率。
[0.1,0.9] , [0.2,0.8], [0.4,0.6],
[0.6,0.4], [0.8,0.2],[0.9,0.1]
所以我们有6种可能的随机行走。注意,概率必须是1,因此考虑 "向上 "或 "向下 "的概率即可。
这里是你如何做的。
x = []
p = [[0.5,0.5],[0.9,0.1],[0.8,0.2],[0.6,0.4],[0.4,0.6],[0.2,0.8],[0.1,0.9]]
label_p = ['Simple',r'$p=0.9$',r'$p=0.8$',r'$p=0.6$',r'$p=0.4$',r'$p=0.2$',r'$p=0.1$']
n = 10000
x = []
for couple in p:
x_p = []
start = 0
for i in range(n):
step = np.random.choice([-1,1],p=couple)
start = start + step
x_p.append(start)
x.append(x_p)
而这是我们将其形象化后的结果。
i=0
for time_series in x:
plt.plot(time_series, label = label_p[i])
i=i+1
plt.xlabel('Steps',fontsize=20)
plt.ylabel(r'$S_{n}$',fontsize=20)
plt.legend()
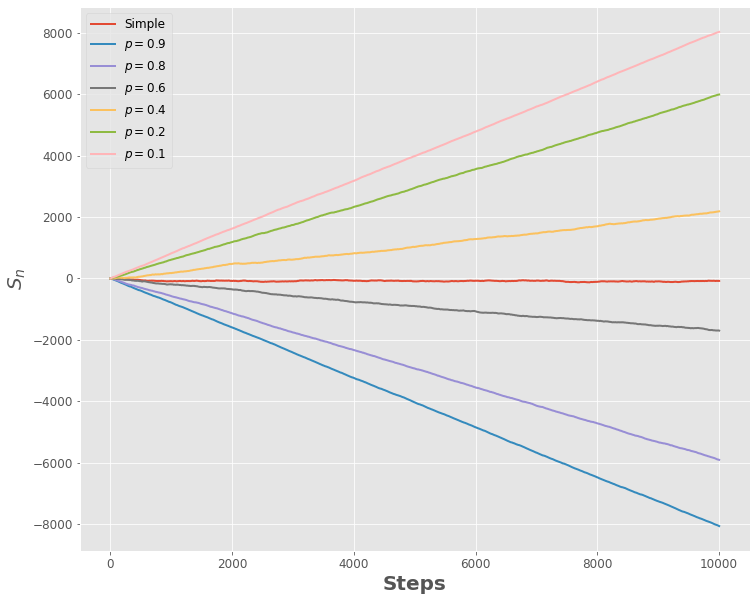
-
赌徒的毁灭链
另一种扩展随机漫步的简单方法是赌徒的毁灭链。 从概念上讲,它与随机漫步非常相似:你从一个状态x开始,你可以以概率p进入一个状态y=x+1,或者以概率1-p进入一个状态y=x-1。
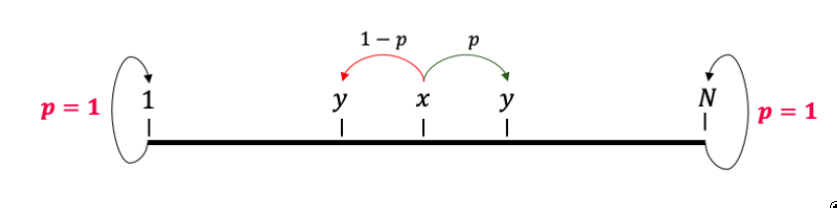
有趣的是,当你到达1或N时,你基本上就被卡住了。你只能永远停留在这个状态下,别无他法。
这个函数给定:
起始点(例如3)
第一个可能的值(例如:0)
和最后一个可能的值(例如:5)
步骤数(如10000)
给你最终的状态。
def gamblersruinchain(start,first,last,n):
for k in range(n):
if start==first or start==last:
start = start
else:
step = np.random.choice([-1,1],p=[0.5,0.5])
start = start + step
return start
现在,在尝试这个函数之前,让我们考虑一个更有趣的情况。
假设我们从状态3开始。两步之后,结束在状态5的概率是多少?
嗯,就是从状态3到状态4,然后再从状态4到状态5的概率。
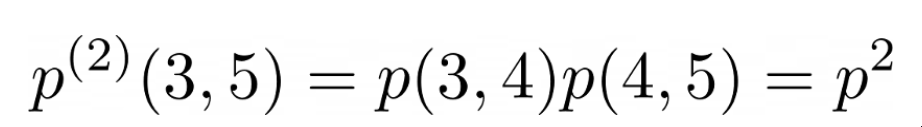
LaTeX制作
在我们的例子中,它只是0.25。
如果现在我们问这个方程。
假设我们从状态3开始。两步之后,结束在状态1的概率是多少?
同样,这是从状态3到状态2,再从状态2到状态1的概率。
唯一的其他选择是在两步之后从状态3到状态3。我们可以用一个非常简单的方法来计算这个概率。由于总的概率必须是1,所以它只是。
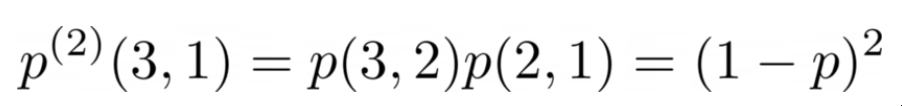
图片由我用LaTeX制作 而如果p=0.5,则又是0.5。
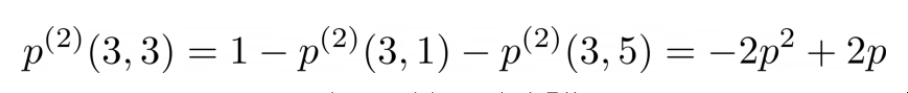
同样,概率的概念是,如果我们无限次地重复一个实验,我们应该能够验证概率值所暗示的发生情况。
state_list = []
for i in range(100000):
state_list.append(gamblersruinchain(3,0,5,2))
data_state = pd.DataFrame({'Final State':state_list})
data_occ = pd.DataFrame(data_state.value_counts('Final State')).rename(columns={0:'Count'})
data_occ['Count'] = data_occ['Count']/100000
sns.barplot(x=data_occ.index,y=data_occ['Count'],palette='plasma')
plt.ylabel('Normalized Count')
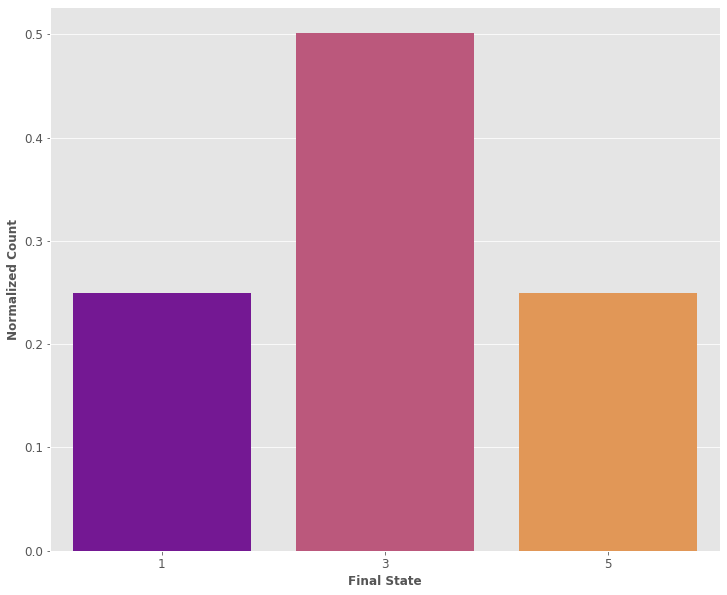
-
自定义马尔科夫链
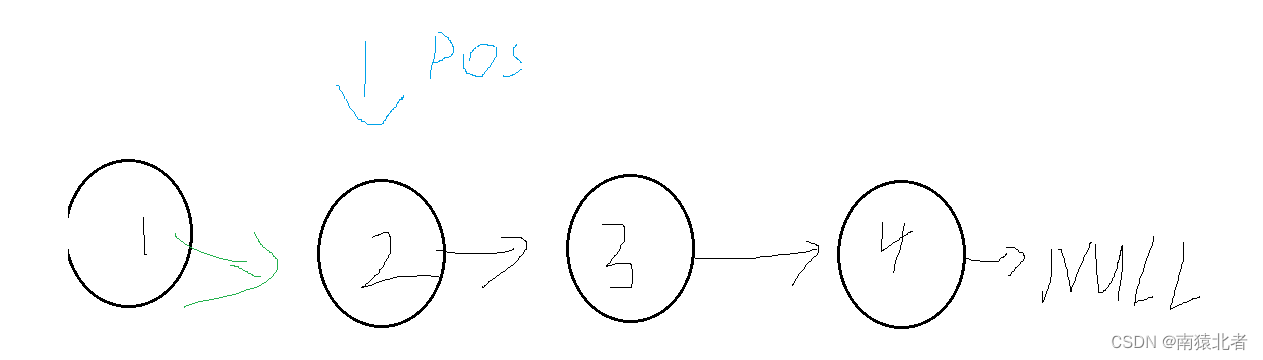
前面的模型是众所周知的,并被用作马尔科夫链的介绍性例子。让我们试着发挥创意,建立一个全新的、不存在的模型,就像下图中的模型。
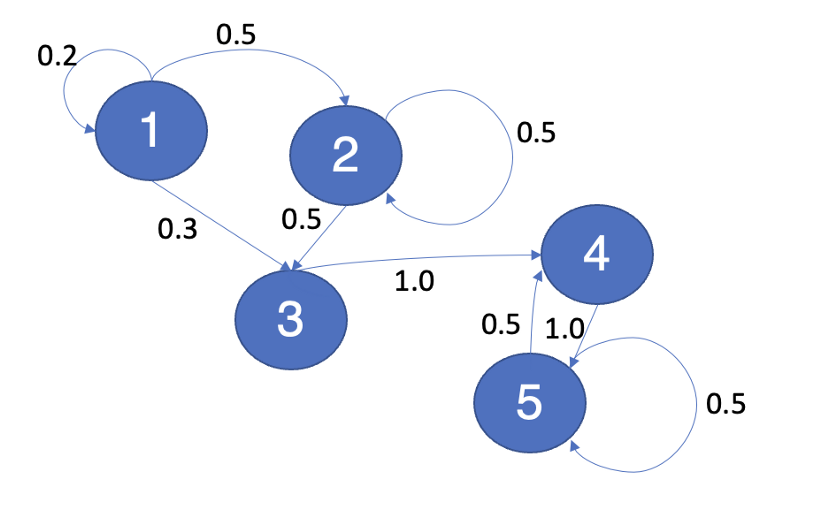
图片由我使用Power Point制作 我是个糟糕的画师,但这个模型本身很简单。
当你看到两个节点(比方说A和B)之间有一个箭头时,这意味着你可以从节点A出发,以一定的概率去到节点B,这个概率是用黑色书写的。
例如,从状态A到状态B的概率是0.5。
一个重要的概念是,模型可以用过渡矩阵来概括,它解释了马尔科夫链中可能发生的一切。这就是我们模型的过渡矩阵。
state_1 = [0.2,0.5,0.3,0,0]
state_2 = [0,0.5,0.5,0,0]
state_3 = [0,0,1,0,0]
state_4 = [0,0,0,0,1]
state_5 = [0,0,0,0.5,0.5]
trans_matrix = [state_1,state_2,state_3,state_4,state_5]
trans_matrix = np.array(trans_matrix)
trans_matrix
array([[0.2, 0.5, 0.3, 0. , 0. ],
[0. , 0.5, 0.5, 0. , 0. ],
[0. , 0. , 1. , 0. , 0. ],
[0. , 0. , 0. , 0. , 1. ],
[0. , 0. , 0. , 0.5, 0.5]])
如果你仔细观察这个模型,你可以看到一些非常特别的东西。比方说,你从状态2跳到状态3。你能回到状态2吗?答案是不能。
同样的情况也适用于状态3和状态1。因此,状态1、3和2被定义为短暂的状态。
另一方面,如果你从状态4开始,总是有可能在某一时刻,你会回到状态4。同样的情况也适用于状态5。这些状态被称为反复出现的状态。
让我们做一些实验,以便我们能够正确理解这个概念。
直观地讲,我们可以看到,从状态2开始,不回到状态2的概率随着步骤数的增加而趋于0。
事实上,从状态2开始,我们在N步之后发现自己处于状态2的概率是如下。
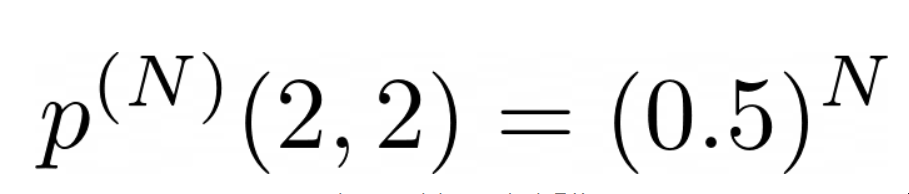
图片由我用LaTeX制作 事实上,如果我们从状态2到状态3,就不可能再回到状态2。让我们把这个理论函数定义为t(N),并把它画出来。
def t(N):
step = np.arange(1,N+1,1)
y = []
for s in step:
v = 0.5**s
y.append(v)
return y
plt.plot(t(10))
plt.ylabel(r'$t(N-1)$',fontsize=20)
plt.xlabel(r'$N-1$',fontsize=20)
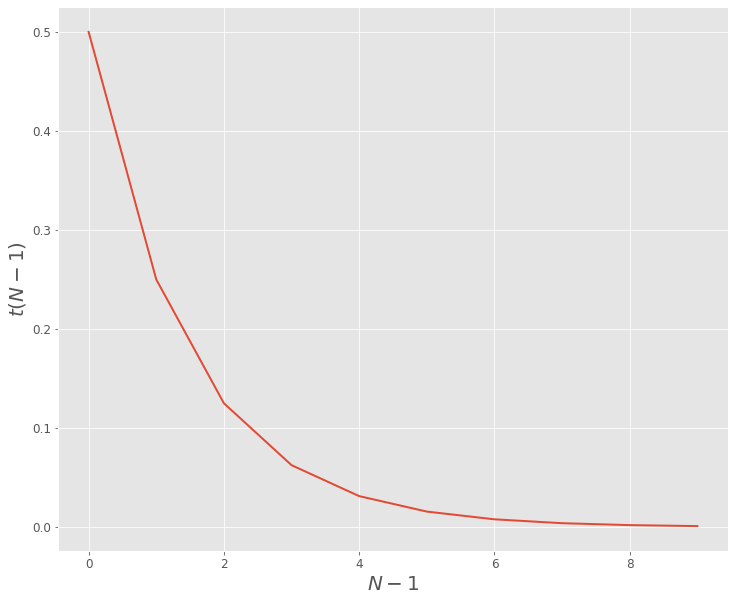
现在,让我们使用马尔科夫链,看看我们是否验证了同样的结果。
我们从状态2开始,在N步之后验证处于状态2的概率。在这种情况下,概率只是最终状态中2的数量与发生次数的比率。为了保持一致,出现的次数需要趋于无穷大。让我们考虑1000次测试。
这就是我们要使用的函数。
def prob(N):
states = np.arange(1,6,1)
steps = np.arange(1,N+1,1)
n=1000
state_collection = []
for k in range(n):
start = 2
for i in range(N):
start = np.random.choice(states,p=trans_matrix[start-1])
if start==2:
state_collection.append(1)
else:
state_collection.append(0)
state_collection = np.array(state_collection)
return state_collection.sum()/n
让我们对各种N使用这个函数,并称其为p(N)。
def p(N):
step = np.arange(1,N+1,1)
y = []
for s in step:
v = prob(s)
y.append(v)
return y
p_20 = p(20)
plt.plot(t(20),label=r'Theory, $t(N-1)$')
plt.plot(p_20,'x',label=r'Simulation, $p(N-1)$',color='navy')
plt.ylabel(r'Result',fontsize=20)
plt.xlabel(r'$N-1$',fontsize=20)
plt.legend()
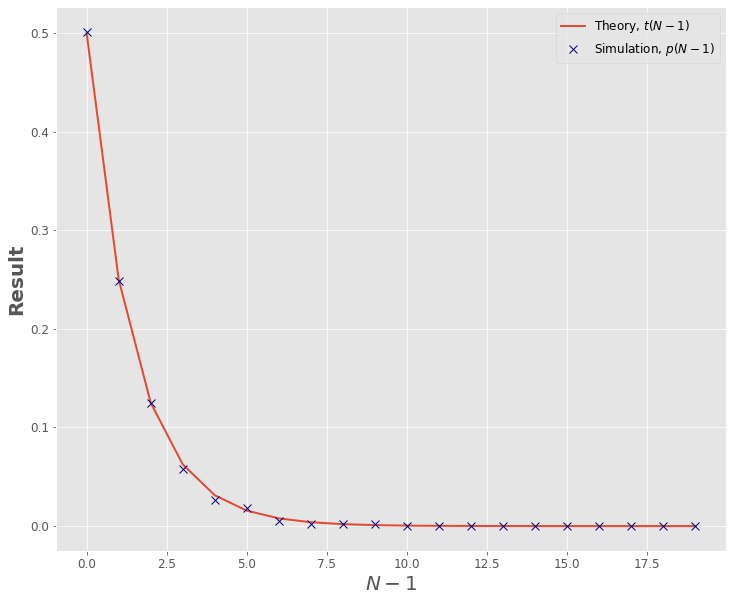
可以看到,我们使用了过渡矩阵来做这个模拟。我们可以使用过渡矩阵来评估我们所考虑的马尔科夫链的所有属性。
-
结论
在这本笔记本中,我们已经看到了非常知名的模型,如随机漫步和赌徒毁灭链。然后,我们创建了自己的全新模型,并对其进行了一番研究,发现了一些重要的概念,如过渡矩阵、循环状态和瞬态。最重要的是,我们已经看到了如何使用Python和非常知名的库以非常简单的方式验证这些概念。
本文由 mdnice 多平台发布