最近看到何同学的视频，拿40部手机花两年半做了关于各种充电的实验视频，视频确实很好看，花里胡哨，看着科技感满满～。但是关于实验设计和根据实验的数据得出最后的结论上似乎有些草率。

实验设计上就不提了，知乎上很多专业人员从电池方面给出了友好的建议，看到很多人诟病何同学没有做显著性分析，本才入行的数据分析师决定用何同学的现有数据帮何同学做个假设检验分析（希望看到后打💰好吧）。

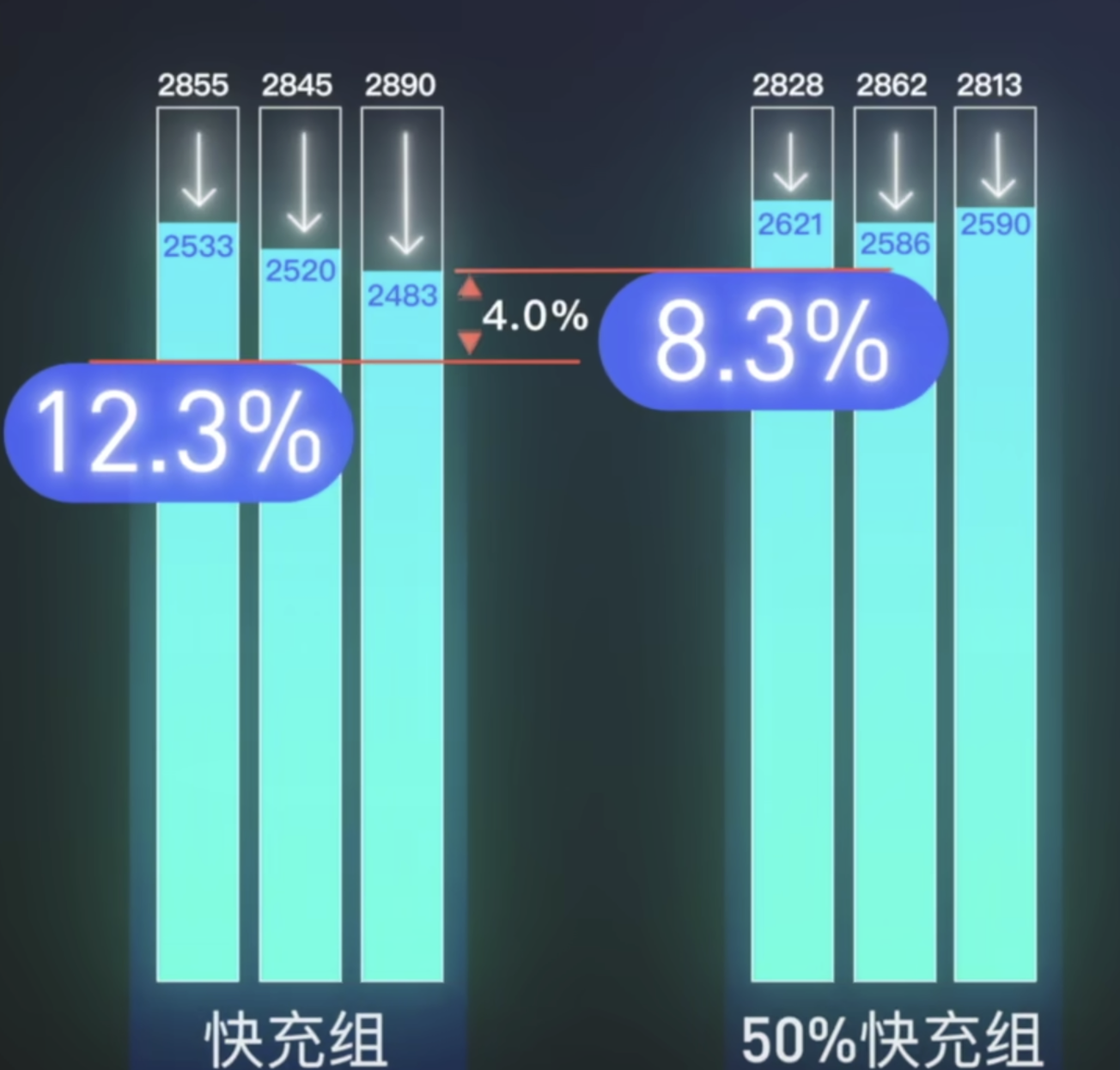
我就拿视频中提到关于iPhone使用的三种充电方式这张图的数据来帮何同学做个分析，得到些合理的结论。

1 明确检验目的，确定检验方法

检验的目的应该是两两比较，查看两种充电方式的损失存储电量有无显著性差异。

由于每组的样本组仅有3个，（这里我们假设各种充电方式的损失存储电量均是符合正态分布的），我们只有选择双样本T检验了。

2 假设检验

导入数据

import pandas as pd
data=pd.read_excel(r"/Users/zrx/Desktop/电池充电实验.xlsx")
data

建立两独立样本t检验的假设

从结果上看，貌似快充组和50%快充组的差异更大，我们以这两组为例进行假设检验。

• H0 : 快充组和50%快充组的损失存储电量的均值是一致的

• H1 : 快充组和50%快充组的损失存储电量的均值是不一致的

方差齐性检验

主要是根据两总体方差是否相等判断使用标准student t检验还是Welch t检验。

from scipy import stats
import numpy as np
sample1=data[data['组别']=='快充组']['diff'].tolist()
sample2=data[data['组别']=='50%快充组']['diff'].tolist()
sample1 = np.asarray(sample1)
sample2 = np.asarray(sample2)
#方差齐性检验
W, P = stats.levene(sample1, sample2, center='mean')
print("方差齐性检验的W统计量为：" + str(W))
print("方差齐性检验的P值为：" + str(P))

P=0.47,说明两组的方差没有显著性差异，应该使用标准student t检验

两独立样本T检验

import statsmodels.stats.weightstats as st
t, p_two, df = st.ttest_ind(sample1, sample2)

print('t=' + str(t))
print('P值=' + str(p_two))
print('自由度=' + str(df))

P=0.03,说明应该拒绝原假设，两组充电方式的损失存储电量是不一致的。

我们再计算一下两者差异的置信区间（95%）：

置信区间通俗点也就是100台iphone手机的话，使用50%快充相比于快充方式，有95台手机都可以提升68-163mAh的存储电量,按照两组之前平均2863mAh的可存储电量计算，可以增加2.38%-5.69%的存储电量。而何同学视频中的4%正在这个范围中。

最后计算一下效应量，显著性检验只是代表显著性差异，在大样本的情况下，一丢丢差异也可以被发现有显著性，比如做上百万次实验，发现上午充电和下午充电对于电池损失电量有显著性差异，但是差异很小，没有实际意义。因此还需要通过计算效应量看看这个变化有无实际含义。

t检验的效应量，我们用Cohen’s d表示，简写为d，反映两个均数之间的标准差异：

计算一下本次实验的效应量：

一般认为（0.20以下：效应过小；0.20-0.50：效应偏小；0.50-0.80：效应较大；0.80以上：大效应）。所以本文计算的3.334是一个很大的效应了。
最后计算一下统计功效：

统计功效=0.81>0.8，犯取伪的错误概率小于20%，还是比较可信的。

感兴趣的同学可以再计算一下，会发现慢充组和快充组是没有显著性差异的。

代码部分参考了 知乎文章

3.总结

何同学在视频中给出的结论是正确的（当然了这些结论是各手机厂商用上千台手机已经验证过的结论），但是从数据到结论缺少了分析过程，数据分析的大忌啊。

以上就是本次文章的全部内容啦。如果你觉得内容还不错的话，求赞求收藏求转发，最重要的是点一个关注，各位的支持就是我写文章的最大动力🫡。

参考链接

• 使用python进行AB测试/两独立样本t检验
• python进行t检验示例
• 第十讲 R-两独立样本t检验
• 科研——关于效应量（effect size）你不知道的那些事儿
• 以Cohen’s d为例浅谈效应量（Effect size）