5. 留数

\quad 如果函数 $f(z)$ 在 $z_0$ 及 $z_0$ 的邻域内处处可导，那么称 $f(z)$ 在点 $z_0$ 处解析。
\quad 如果函数 $f(z)$ 在点 $z_0$ 处不解析，那么 $z_0$ 为 $f(z)$ 的奇点。

定义　如果函数 $f(z)$ 在 $z_0$ 不解析，但是在 $z_0$ 的某个去心邻域 $0<|z-z_0|<\delta$ 内处处解析，那么 $z_0$ 称为 $f(z)$ 的孤立奇点。

\quad 例如，函数 $\frac{1}{z},e^{\frac{1}{z}}$ 都以 $z=0$ 为孤立奇点；当 $z=\infty$ 为孤立奇点，其去心邻域为 $R<|z|<+\infty$。

5.1 可去奇点、极点、本性奇点

\quad 由洛朗级数的定义可知，函数 $f(z)$ 在其孤立奇点 $z_0$ 的去心邻域内可以展开成洛朗级数。根据展开式的不同情况，可以将孤立奇点划分为可去奇点、极点和本性奇点：

$(1)$ 如果 $z_0$ 为 $f(z)$ 的可去奇点，那么 $\underset{z\to z_0}{\lim }f(z)$ 存在、且有限
$(2)$ 如果 $z_0$ 为 $f(z)$ 的极点，那么 $\underset{z\to z_0}{\lim }f(z)=\infty$
$(3)$ 如果 $z_0$ 为 $f(z)$ 的本性奇点，$\underset{z\to z_0}{\lim }f(z)$ 不存在、且不为 $\infty$

$\bullet$可去奇点

定义　如果在洛朗级数中不含 $z-z_0$ 的负幂项，那么孤立奇点 $z_0$ 称为 $f(z)$ 的可去奇点。

\quad 此时，$f(z)$ 在 $z_0$ 的去心邻域内的洛朗级数，就是一个普通幂级数

\qquad\qquad $f(z)=c_0+c_1(z-z_0)+\cdots +c_n(z-z_0{)}^n+\cdots$

\quad 因此，该幂级数的和函数 $F(z)$ 是在 $z_0$ 解析的函数，且当 $z\ne z_0$ 时，$F(z)=f(z)$；当 $z=z_0$ 时，$F(z_0)=c_0$。

\quad 由于 $\underset{z\to z_0}{\lim }f(z)=\underset{z\to z_0}{\lim }F(z)=F(z_0)=c_0$，所以不论 $f(z)$ 原来在 $z_0$ 处是否有定义，如果我们令 $f(z_0)=c_0$，那么在圆域 $|z-z_0|<\delta$ 内就有 $f(z)=c_0+c_1(z-z_0)+\cdots +c_n(z-z_0{)}^n+\cdots$，从而函数 $f(z)$ 在 $z_0$ 处就成为解析的。

例如，$z=0$ 是 $\frac{\sin z}{z}$ 的可去奇点
在 $z=0$ 的去心邻域内的洛朗级数 $\frac{\sin z}{z}=\frac{1}{z}\left(z-\frac{1}{3!}{z}^3+\frac{1}{5!}{z}^5-\cdots \right)=1-\frac{1}{3!}{z}^2+\frac{1}{5!}{z}^4-\cdots$ 不含负幂项
如果我们令 $\frac{\sin z}{z}$ 在 $z=0$ 的值为 $1$，即 $c_0=1$，那么 $\frac{\sin z}{z}$ 在 $z=0$ 就成为解析的。

$\bullet$极点

定义　如果在洛朗级数中只有有限多个 $z-z_0$ 的负幂项，且其中关于 $(z-z_0{)}^{-1}$ 的最高幂为 $(z-z_0{)}^{-m}$，那么孤立奇点 $z_0$ 称为 $f(z)$ 的 $m$ 级极点。

\quad 即：　$f(z)=c_{-m}(z-z_0{)}^{-m}+\cdots +c_{-2}(z-z_0{)}^{-2}+c_{-1}(z-z_0{)}^{-1}+c_0+c_1(z-z_0)+\cdots$

\quad 上式也可以写成：　$f(z)=\frac{g(z)}{(z-z_0{)}^m}$

\quad 且　　　　　　　 $g(z)=c_{-m}+c_{-m+1}(z-z_0)+c_{-m+2}(z-z_0{)}^2+\cdots$

\quad 其中，$g(z)$ 是 $|z-z_0|<\delta$ 内的解析函数（不含负幂项），且 $g(z_0)\ne 0$
　
$▶$　反过来，当任一函数可以表示为 $f(z)=\frac{g(z)}{(z-z_0{)}^m}$，且 $g(z_0)\ne 0$ 时，那么 $z_0$ 是函数 $f(z)$ 的 $m$ 级极点。

$▶$　如果 $z_0$ 为 $f(z)$ 的极点，由 $f(z)=\frac{g(z)}{(z-z_0{)}^m}$，就有 $\underset{z\to z_0}{\lim }|f(z)|=+\infty$ 或 $\underset{z\to z_0}{\lim }f(z)=\infty$

例如，对于有理分式函数 $f(z)=\frac{z-2}{(z^2+1)(z-1{)}^3}$，$z=1$ 是一个 $3$ 级极点，$z=\pm \text{i}$ 是 $1$ 级极点。

$\bullet$本性极点

定义　如果在洛朗级数中含有无穷多个 $z-z_0$ 的负幂项，那么孤立奇点 $z_0$ 称为 $f(z)$ 的本性奇点。

\quad 如果 $z_0$ 为函数 $f(z)$ 的本性奇点，那么对于任意给定的复数 $A$，总可以找到一个趋于 $z_0$ 的数列，当 $z$ 沿这个数列趋向于 $z_0$ 时，$f(z)\to A$。

\quad 例如，由于 $e^{\frac{1}{z}}=1+z^{-1}+\frac{1}{2!}{z}^{-2}+\cdots +\frac{1}{n!}{z}^{-n}+\cdots$ 中有无穷多个 $z$ 的负幂项，因此函数 $f(z)=e^{\frac{1}{z}}$ 以 $z=0$ 为它的本性奇点。
\quad

5.2 零点与极点的关系

定义　不恒等于零的解析函数 $f(z)$ 如果能表示成 $f(z)=(z-z_0{)}^m\phi (z)$，其中 $\phi (z)$ 在 $z_0$ 解析并且 $\phi (z_0)\ne 0$，$m$ 为正整数，那么 $z_0$ 称为函数 $f(z)$ 的 $m$ 级零点。
　
定理　如果 $f(z)$ 在 $z_0$ 解析，那么 $z_0$ 是 $f(z)$ 的 $m$ 级零点的充要条件是：$f^{(n)}(z_0)=0(n=0,1,\cdots ,m-1),f^{(m)}(z_0)\ne 0$。

证：将 $\phi (z)$ 在 $z_0$ 处展开成泰勒级数：$\phi (z)=c_0+c_1(z-z_0)+c_2(z-z_0{)}^2+\cdots$，且 $c_0\ne 0$
由 $f(z)=(z-z_0{)}^m\phi (z)$ 可得到 $f(z)$ 在 $z_0$ 处的泰勒级数为：
　$f(z)=c_0(z-z_0{)}^m+c_1(z-z_0{)}^{m+1}+c_2(z-z_0{)}^{m+2}+\cdots$，第 $n$ 项的系数为 $\frac{f^{(n)}(z_0)}{n!}$
显然，前 $m$ 项系数都为零，即 $f^{(n)}(z_0)=0(n=0,1,\cdots ,m-1)$，而 $\frac{f^{(m)}(z_0)}{m!}=c_0\ne 0$

例如，$z=0,z=1$ 分别是函数 $f(z)=z(z-1{)}^3$ 的 $1$ 级和 $3$ 级零点
例如，$z=1$ 是函数 $f(z)=z^3-1$ 的 $1$ 级零点，由于 $f^{\prime }(1)=3z^2{|}_{z=1}=3\ne 0$
　
$★$一个不恒等于零的解析函数的零点是孤立的。

\quad 由于 $\phi (z)$ 在 $z_0$ 解析并且 $\phi (z_0)\ne 0$，因此 $\phi (z)$ 在 $z_0$ 邻域内不为零，从而 $f(z)=(z-z_0{)}^m\phi (z)$ 在 $z_0$ 的去心邻域内不为零（只在 $z_0$ 处为零）。

由于 $\phi (z)$ 在 $z_0$ 解析，那么 $\phi (z)$ 在 $z_0$ 连续，即 $\underset{z\to z_0}{\lim }\phi (z)=\phi (z_0)$，由极限定义
若令 $\epsilon =\frac{1}{2}|\phi (z_0)|$，必存在 $\delta >0$，当 $|z-z_0|<\delta$ 时，有 $|\phi (z)-\phi (z_0)|<\epsilon =\frac{1}{2}|\phi (z_0)|$
由此得到 $|\phi (z)|>\frac{1}{2}|\phi (z_0)|$，因此 $\phi (z)$ 在 $z_0$ 邻域内不为零

定理　如果 $z_0$ 是函数 $f(z)$ 的 $m$ 级极点，那么 $z_0$ 就是 $\frac{1}{f(z)}$ 的 $m$ 级零点；反之也成立。
\quad

5.3 在无穷远点处的情形

\quad 如果函数 $f(x)$ 在无穷远点 $z=\infty$ 的去心邻域 $R<|z|<+\infty$ 内解析，那么称点 $\infty$ 为 $f(x)$ 的孤立奇点。

\quad 分析方法：做变换 $t=\frac{1}{z}$，那么
$(1)$ 扩充 $z$ 平面上的无穷远点 $z=\infty$，映射成扩充 $t$ 平面上的点 $t=0$
$(2)$ 扩充 $z$ 平面上无穷远点 $z=\infty$ 的去心邻域 $R<|z|<+\infty$，映射成扩充 $t$ 平面上原点的去心邻域 $0<|t|<\frac{1}{R}$

\quad 若令 $f(z)=f(\frac{1}{t})=\phi (t)$，就可以把在去心邻域 $R<|z|<+\infty$ 内、对函数 $f(z)$ 的研究转化为在去心邻域 $0<|t|<\frac{1}{R}$ 内、对函数 $\phi (t)$ 的研究。由于 $f(x)$ 在无穷远点 $z=\infty$ 的去心邻域 $R<|z|<+\infty$ 内解析，那么 $\phi (t)$ 在去心邻域 $0<|t|<\frac{1}{R}$ 内也是解析的，所以 $t=0$ 是 $\phi (t)$ 的可去奇点。

\quad 由于 $f(x)$ 在圆环域 $R<|z|<+\infty$ 内解析，在该圆环域内的洛朗级数展开式为（其中，$C$ 为该圆环域内绕原点的任何一条正向简单闭曲线）：

$\begin{array}{rl}f(z)& =\sum _{n=1}^{\infty }{c}_{-n}{z}^{-n}+\sum _{n=0}^{\infty }{c}_n{z}^n\\ & =\sum _{n=1}^{\infty }{c}_{-n}{z}^{-n}+c_0+\sum _{n=1}^{\infty }{c}_n{z}^n,c_n=\frac{1}{2\pi \text{i}}{\oint }_C\frac{f(\zeta )}{{\zeta }^{n+1}}\mathrm{d}\zeta (n=0,\pm 1,\pm 2,\cdots )\end{array}$

\quad 由 $t=z^{-1}$，$\phi (t)$ 在圆环域 $0<|t|<\frac{1}{R}$ 内解析，在该圆环域内的洛朗级数展开式为：

$\phi (t)=\sum _{n=1}^{\infty }{c}_{-n}{t}^n+c_0+\sum _{n=1}^{\infty }{c}_n{t}^{-n}$

\quad 由 5.1 可知，在 $\phi (t)$ 的洛朗级数展开式中
$(1)$ 若不含负项幂，则 $t=0$ 是 $\phi (t)$ 的可去奇点
$(2)$ 若含有有限多的负项幂，且 $t^{-m}$ 为最高负幂，则 $t=0$ 是 $\phi (t)$ 的 $m$ 级极点
$(3)$ 若含有无限多的负项幂，则 $t=0$ 是 $\phi (t)$ 的本性奇点

\quad 由 $\phi (t)$ 与 $f(x)$ 的关系，可得到在 $f(x)$ 的洛朗级数展开式中就有：
$(1)$ 若不含正项幂，则 $z=\infty$ 是 $f(x)$ 的可去奇点
$(2)$ 若含有有限多的正项幂，且 $z^m$ 为最高正幂，则 $z=\infty$ 是 $f(x)$ 的 $m$ 级极点
$(3)$ 若含有无限多的正项幂，则 $z=\infty$ 是 $f(x)$ 的本性奇点
\quad

5.4 留数

\quad 如果 $f(z)$ 在 $z_0$ 的邻域内解析，由柯西-古萨基本定理，就有 ${\oint }_{C}f(z)\mathrm{d}z=0$，其中 $C$ 为 $z_0$ 邻域内的任意一条简单闭曲线。

$\bullet$留数

\quad 如果 $z_0$ 为 $f(z)$ 的一个孤立奇点，那么沿着在 $z_0$ 的某个去心邻域 $R<|z|<+\infty$ 内、包含 $z_0$ 的任意一条正向简单闭曲线 $C$ 的积分 ${\oint }_{C}f(z)\mathrm{d}z$ 一般不等于零，为了计算该积分：

$(1)$ 首先，将函数 $f(z)$ 在该圆环域 $R<|z|<+\infty$ 内展开成洛朗级数：

$\begin{array}{rl}f(z)=& \cdots +c_{-n}(z-z_0{)}^{-n}+\cdots +c_{-1}(z-z_0{)}^{-1}\\ & +c_0+c_1(z-z_0)+\cdots +c_n(z-z_0{)}^n+\cdots \end{array}$

$(2)$ 然后，再对此洛朗级数的展开式的两端沿 $C$ 逐项积分：除了对 $c_{-1}(z-z_0{)}^{-1}$ 项的积分等于 $2\pi \text{i}{c}_{-1}$ 之外，其余项的积分都为零（由复合闭路定理及2.1节例题结论），即：${\oint }_{C}f(z)\mathrm{d}z=2\pi \text{i}{c}_{-1}$。

$(3)$ 把（留下的）这个积分值除以 $2\pi \text{i}$ 后所得的数，称为函数 $f(z)$ 在 $z_0$ 的留数，记为 $\text{Res}[f(z),z_0]$，即

$\text{Res}[f(z),z_0]=\frac{1}{2\pi \text{i}}{\oint }_{C}f(z)\mathrm{d}z=c_{-1}$

\qquad

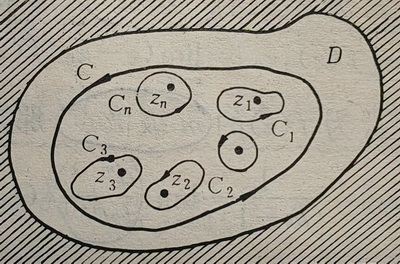
留数定理 设函数 $f(z)$ 在区域 $D$ 内除有限个孤立奇点 $z_1,z_2,\cdots ,z_n$ 外处处解析，$C$ 是 $D$ 内包围各个奇点的一条正向简单闭曲线，那么
${\oint }_{C}f(z)\mathrm{d}z=2\pi \text{i}\sum _{k=1}^n\text{Res}[f(z),z_k]$

证： 在上图中，把在 $C$ 内的所有孤立奇点 $z_k$ 用互不包含的正向简单曲线 $C_k$ 包围起来
由复合闭路定理可得：${\oint }_{C}f(z)\mathrm{d}z={\oint }_{C_1}f(z)\mathrm{d}z+{\oint }_{C_2}f(z)\mathrm{d}z+\cdots +{\oint }_{C_n}f(z)\mathrm{d}z$
两边都除以$2\pi \text{i}$，可得 $\frac{1}{2\pi \text{i}}{\oint }_{C}f(z)\mathrm{d}z=\text{Res}[f(z),z_1]+\text{Res}[f(z),z_2]+\cdots +\text{Res}[f(z),z_n]$

$★$利用留数定理，求沿封闭曲线 $C$ 的积分，就转化为求被积函数在 $C$ 中的各孤立奇点处的留数。
　
$\bullet$留数的计算规则

规则1 如果 $z_0$ 为 $f(z)$ 的一级极点，那么 $\text{Res}[f(z),z_0]=\underset{z\to z_0}{\lim }(z-z_0)f(z)$

规则2 如果 $z_0$ 为 $f(z)$ 的 $m$ 级极点，那么 $\text{Res}[f(z),z_0]=\frac{1}{(m-1)!}\underset{z\to z_0}{\lim }\frac{{\mathrm{d}}^{m-1}}{\mathrm{d}{z}^{m-1}}\{(z-z_0{)}^{m}f(z)\}$

证：由 $f(z)=c_{-m}(z-z_0{)}^{-m}+\cdots +c_{-1}(z-z_0{)}^{-1}+c_0+c_1(z-z_0)+\cdots$
两边乘以 $(z-z_0{)}^m$ 得到
　　$(z-z_0{)}^{m}f(z)=c_{-m}+c_{-m+1}(z-z_0)+\cdots +c_{-1}(z-z_0{)}^{m-1}+c_0(z-z_0{)}^m+\cdots$
两边求 $m-1$ 阶导数，得 d m − 1 d z m − 1 { ( z − z 0 ) m f ( z ) } = ( m − 1 ) ! c − 1 + { \dfrac{\mathrm{d}^{m-1}}{\mathrm{d}z^{m-1}}\{(z-z_0)^mf(z)\}=(m-1)!c_{-1}+\{ dzm−1dm−1​{(z−z0​)mf(z)}=(m−1)!c−1​+{含有$z-z_0$正幂的项$\}$
令 $z\to z_0$ 两端求极限，$\underset{z\to z_0}{\lim }\frac{{\mathrm{d}}^{m-1}}{\mathrm{d}{z}^{m-1}}\{(z-z_0{)}^{m}f(z)\}=(m-1)!c_{-1}$
可得 $\text{Res}[f(z),z_0]=\frac{1}{2\pi \text{i}}{\oint }_{C}f(z)\mathrm{d}z=c_{-1}=\frac{1}{(m-1)!}\underset{z\to z_0}{\lim }\frac{{\mathrm{d}}^{m-1}}{\mathrm{d}{z}^{m-1}}\{(z-z_0{)}^{m}f(z)\}$

规则3 设 $f(z)=\frac{P(z)}{Q(z)}$，$P(z)$ 和 $Q(z)$ 在 $z_0$ 都解析，如果 $P(z_0)\ne 0$，$Q(z_0)=0$，$Q^{\prime }(z_0)\ne 0$
　　　那么 $z_0$ 为 $f(z)$ 的一级极点，且 $\text{Res}[f(z),z_0]=\frac{P(z_0)}{Q^{\prime }(z_0)}$

---

例. 计算积分 ${\oint }_C\frac{z{e}^z}{z^2-1}\mathrm{d}z$，$C$ 为正向圆周：$|z|=2$
由于 $f(z)$ 有两个一级极点 $+1,-1$，且极点都在 $C$ 内，由规则1
∮ C z e z z 2 − 1 d z = 2 π i {  Res [ f ( z ) , + 1 ] + Res [ f ( z ) , − 1 ]   } = 2 π i {   lim ⁡ z → 1 ( z − 1 ) z e z z 2 − 1 + lim ⁡ z → − 1 ( z + 1 ) z e z z 2 − 1 } = 2 π i {   lim ⁡ z → 1 z e z z + 1 + lim ⁡ z → − 1 z e z z − 1 } = π i ( e + e − 1 ) \begin{aligned}\displaystyle\oint_C\dfrac{ze^z}{z^2-1}\mathrm{d}z&=2\pi\text{i}\{\ \text{Res}[f(z),+1]+\text{Res}[f(z),-1]\ \} \\ &=2\pi\text{i}\{\ \lim_{z\to 1}(z-1)\dfrac{ze^z}{z^2-1} +\lim_{z\to -1}(z+1)\dfrac{ze^z}{z^2-1}\} \\ &=2\pi\text{i}\{\ \lim_{z\to 1}\dfrac{ze^z}{z+1} +\lim_{z\to -1}\dfrac{ze^z}{z-1} \} \\ &=\pi\text{i}(e+e^{-1}) \end{aligned} ∮C​z2−1zez​dz​=2πi{ Res[f(z),+1]+Res[f(z),−1] }=2πi{ z→1lim​(z−1)z2−1zez​+z→−1lim​(z+1)z2−1zez​}=2πi{ z→1lim​z+1zez​+z→−1lim​z−1zez​}=πi(e+e−1)​
或者由规则3
∮ C z e z z 2 − 1 d z = 2 π i {  Res [ f ( z ) , + 1 ] + Res [ f ( z ) , − 1 ]   } = 2 π i {   z e z 2 z ∣ z = + 1 + z e z 2 z ∣ z = − 1 } = π i ( e + e − 1 ) \begin{aligned}\displaystyle\oint_C\dfrac{ze^z}{z^2-1}\mathrm{d}z&=2\pi\text{i}\{\ \text{Res}[f(z),+1]+\text{Res}[f(z),-1]\ \} \\ &=2\pi\text{i}\{\ \dfrac{ze^z}{2z}\big|_{z=+1} +\dfrac{ze^z}{2z}\big|_{z=-1}\} \\ &=\pi\text{i}(e+e^{-1}) \end{aligned} ∮C​z2−1zez​dz​=2πi{ Res[f(z),+1]+Res[f(z),−1] }=2πi{ 2zzez​ ​z=+1​+2zzez​ ​z=−1​}=πi(e+e−1)​

---

例. 计算积分 ${\oint }_C\frac{e^z}{z(z-1{)}^2}\mathrm{d}z$，$C$ 为正向圆周：$|z|=2$
由于 $f(z)$ 有一级极点 $z=0$，有二级极点 $z=1$，且极点都在 $C$ 内，由规则1和规则2
∮ C z e z z 2 − 1 d z = 2 π i {  Res [ f ( z ) , 0 ] + Res [ f ( z ) , 1 ]   } = 2 π i {   lim ⁡ z → 0 z e z z ( z − 1 ) 2 + lim ⁡ z → 1 d d z { ( z − 1 ) 2 e z z ( z − 1 ) 2 } } = 2 π i {   1 + lim ⁡ z → 1 d d z { e z z } } = 2 π i (   1 + lim ⁡ z → 1 e z z − e z z 2 ) = 2 π i \begin{aligned}\displaystyle\oint_C\dfrac{ze^z}{z^2-1}\mathrm{d}z&=2\pi\text{i}\{\ \text{Res}[f(z),0]+\text{Res}[f(z),1]\ \} \\ &=2\pi\text{i}\{\ \lim_{z\to 0}z\dfrac{e^z}{z(z-1)^2} +\lim_{z\to 1}\dfrac{\mathrm{d}}{\mathrm{d}z}\{(z-1)^2\dfrac{e^z}{z(z-1)^2}\}\} \\ &=2\pi\text{i}\{\ 1 +\lim_{z\to 1}\dfrac{\mathrm{d}}{\mathrm{d}z}\{\dfrac{e^z}{z}\} \} \\ &=2\pi\text{i}(\ 1 +\lim_{z\to 1}\dfrac{e^zz-e^z}{z^2} ) \\ &=2\pi\text{i} \end{aligned} ∮C​z2−1zez​dz​=2πi{ Res[f(z),0]+Res[f(z),1] }=2πi{ z→0lim​zz(z−1)2ez​+z→1lim​dzd​{(z−1)2z(z−1)2ez​}}=2πi{ 1+z→1lim​dzd​{zez​}}=2πi( 1+z→1lim​z2ezz−ez​)=2πi​
　
$\bullet$在无穷远点的留数

定义 设函数 $f(x)$ 在圆环域 $R<|z|<+\infty$ 内解析，$C$ 为圆环域内绕原点的任何一条正向简单闭曲线，那么 $\frac{1}{2\pi \text{i}}{\oint }_{C^{-}}f(z)\mathrm{d}z$ 的值与 $C$ 无关，称此定值为 $f(x)$ 在无穷远点 $\infty$ 的留数，记作 $\text{Res}[f(z),\infty ]=\frac{1}{2\pi \text{i}}{\oint }_{C^{-}}f(z)\mathrm{d}z$。

在5.3中，$f(x)$ 在圆环域 $R<|z|<+\infty$ 内解析，在该圆环域内的洛朗级数展开式为（$C$ 为该圆环域内绕原点的任何一条正向简单闭曲线）：
$\begin{array}{rl}f(z)& =\sum _{n=1}^{\infty }{c}_{-n}{z}^{-n}+c_0+\sum _{n=1}^{\infty }{c}_n{z}^n,c_n=\frac{1}{2\pi \text{i}}{\oint }_C\frac{f(\zeta )}{{\zeta }^{n+1}}\mathrm{d}\zeta (n=0,\pm 1,\pm 2,\cdots )\end{array}$

\quad 显然，当 $n=-1$ 时，$c_{-1}=\frac{1}{2\pi \text{i}}{\oint }_{C}f(\zeta )\mathrm{d}\zeta$。
\quad 因此，$f(x)$ 在无穷远点 $\infty$ 的留数 $\text{Res}[f(z),\infty ]=-c_{-1}$。
　
定理 如果函数 $f(z)$ 在扩充复平面内只有有限个孤立奇点，那么 $f(z)$ 在所有各奇点（包括无穷远点$\infty$）的留数的总和必等于零。

除无穷远点$\infty$之外，设 $f(z)$ 的有限个奇点为 $z_k(k=1,\cdots ,n)$，又设 $C$ 为一条绕原点的、并将 $z_k(k=1,\cdots ,n)$ 包含在内部的正向简单闭曲线。
根据留数定理 ${\oint }_{C}f(z)\mathrm{d}z=2\pi \text{i}\sum _{k=1}^n\text{Res}[f(z),z_k]$
以及无穷远点的留数定义 ${\oint }_{C^{-}}f(z)\mathrm{d}z=2\pi \text{i}\text{Res}[f(z),\infty ]$
因此 $\text{Res}[f(z),\infty ]+\sum _{k=1}^n\text{Res}[f(z),z_k]=\frac{1}{2\pi \text{i}}{\oint }_{C^{-}}f(z)\mathrm{d}z+\frac{1}{2\pi \text{i}}{\oint }_{C}f(z)\mathrm{d}z=0$

规则4 关于无穷远点的留数计算，有 $\text{Res}[f(z),\infty ]=-\text{Res}\left[f\left(\frac{1}{z}\right)\frac{1}{z^2},0\right]$

例. 计算积分 ${\oint }_C\frac{z}{z^4-1}\mathrm{d}z$，$C$ 为正向圆周：$|z|=2$
由于 $f(z)$ 在 $|z|=2$ 的外部，除了无穷远点$\infty$之外，没有其他奇点，由本节定理和规则4
$\begin{array}{rl}{\oint }_C\frac{z}{z^4-1}\mathrm{d}z& =-2\pi \text{i}\text{Res}[f(z),\infty ]\\ & =2\pi \text{i}\text{Res}\left[f\left(\frac{1}{z}\right)\frac{1}{z^2},0\right]\\ & =2\pi \text{i}\text{Res}\left[\frac{z}{1-z^4},0\right]=0\end{array}$