1. 摘要

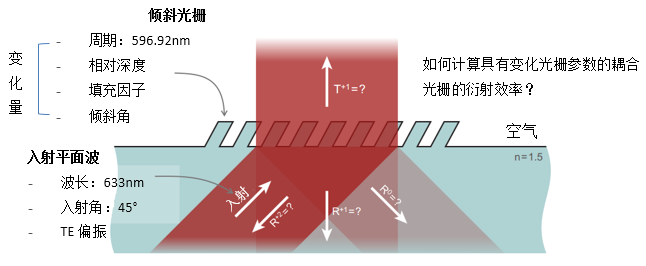
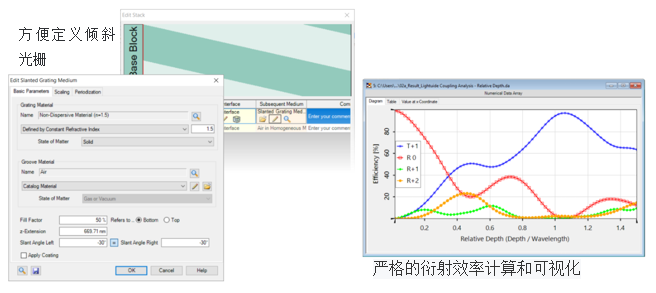
因其在确定衍射级上的高衍射效率，倾斜光栅广泛用于将光耦合到光波导中。如今，倾斜光栅广泛用于增强现实和混合现实应用中。本示例中将示范如何使用VirtualLab Fusion分析文献中具有特定参数的某些倾斜光栅的几何形状（例如倾斜角、填充因子和调制深度）。 另外，研究了不同入射角对衍射效率的影响。
 

2. 建模任务
 

  

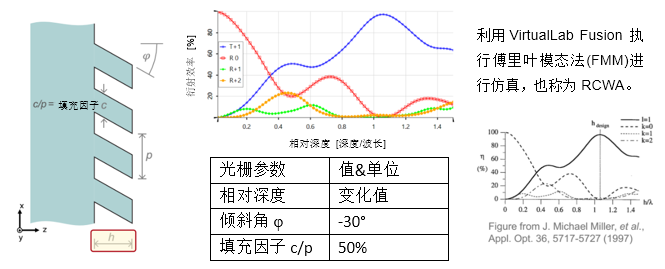
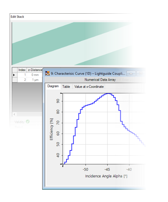
3. 衍射效率vs.相对深度
 

4. 衍射效率vs.倾斜角
 

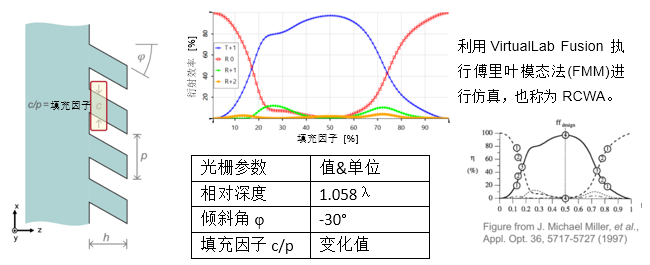
5. 衍射效率vs. 填充因子

 

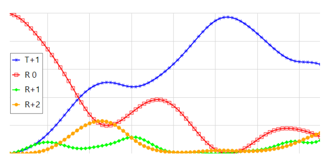
6. 衍射效率vs.变化的入射角

7. 走进VirtualLab Fusion
 

8. VirtualLab Fusion 的工作流程

• 光波导耦合光栅结构的配置

• 倾斜光栅的高级配置 [使用案例]
• 使用特殊材料的光栅结构配置 [使用案例]
• 使用界面的光栅结构配置 [使用案例]

• 耦合光栅衍射效率分析

• 自定义的光波导耦合光栅评价探测器 [使用案例]

• 通过扫描特定的参数来检查效率

• 参数运行的使用 [使用案例]

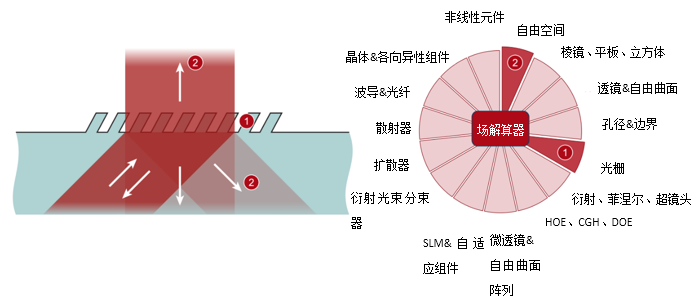
9. VirtualLab Fusion 技术
 

10. 文件信息