K-Means

K-Means聚类又叫K均值聚类，是一种线性时间复杂度的聚类方法，也是比较成熟的一种聚类算法。
在这里插入图片描述
具体计算步骤如上。

Silhouette Coefficient（轮廓系数）

在"无监督学习" (unsupervised learning) 中，训练样本的标记信息是未知的，目标是通过对无标记训练样本的学习来揭示数据的内在性质及规律，为进一步的数据分析提供基础。聚类结果的"簇内相似度" (intra-cluster similarity) 高且"簇间相似度" (inter-cluster similarity)被认为是比较好的聚类结果。

sklearn中对轮廓系数法的说明如下：
The Silhouette Coefficient is calculated using the mean intra-cluster
distance (a) and the mean nearest-cluster distance (b) for eachsample.
The Silhouette Coefficient for a sample is (b - a) / max(a, b).
To clarify, b is the distance between a sample and the nearestcluster that the sample is not a part of.
Note that Silhouette Coefficient is only defined if number of labelsis 2 <= n_labels <= n_samples - 1.

计算公式如下：
在这里插入图片描述

其中a(i)表示同簇相似度，计算方式为：
在这里插入图片描述

其中b(i)表示不同簇之间的不相似度，计算方式如下：
在这里插入图片描述
因此，轮廓系数取值为：

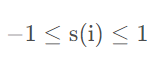
也就是说明s(i)越大说明聚类效果越好。

代码实现

data4.0:

密度,含糖率
0.697,0.46
0.774,0.376
0.634,0.264
0.608,0.318
0.556,0.215
0.403,0.237
0.481,0.149
0.437,0.211
0.666,0.091
0.243,0.267
0.245,0.057
0.343,0.099
0.639,0.161
0.657,0.198
0.36,0.37
0.593,0.042
0.719,0.103
0.359,0.188
0.339,0.241
0.282,0.257
0.748,0.232
0.714,0.346
0.483,0.312
0.478,0.437
0.525,0.369
0.751,0.489
0.532,0.472
0.473,0.376
0.725,0.445
0.446,0.459

# -*- coding: utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
from sklearn import metrics
import pandas as pd
f = pd.read_csv("data4.0.csv")
 
def kmeans(data, center_ids, max_err=0.00001, max_round=100):
    process = []
    init_centers = []
    n = len(center_ids)
    for id in center_ids:
        init_centers.append(data[id, :])
    error, rounds = 1.0, 0
    while error > max_err and rounds < max_round:
        rounds += 1
        clusters = []
        for _ in range(n):
            clusters.append([])
        for j in range(len(data)):
            dist = []
            for i in range(n):
                vector = data[j, :] - init_centers[i]
                d_ji = np.dot(vector, vector) ** 0.5
                dist.append(d_ji)
            near_id = sorted(enumerate(dist), key=lambda x: x[1])[0][0]
            clusters[near_id].append(j)
 
        new_center = [0] * n
        error = 0
        for i in range(n):
            new_center[i] = np.sum(data[clusters[i], :], axis=0)
            new_center[i] /= len(clusters[i])
            vec = new_center[i] - init_centers[i]
            err = np.dot(vec, vec) ** 0.5
            if err:
                init_centers[i] = new_center[i]
                error += err

        data_ = np.zeros(data.shape)
        label_ = np.zeros(len(data))
        start = 0
        for i in range(len(center_ids)):
            num = len(clusters[i]) + start
            data_[start:num] = data[clusters[i]]
            label_[start:num] = i
            start = num
        label_ = label_.astype("int")
        process.append([data_, label_, new_center, rounds])  # 记录训练过程

    return process[-1] # 最后一次就是我们需要的结果


best_k = []
N = 10 # 最多10类
for n in range(2, N + 1): # 从2-10中寻找最佳k值
    data = f.values
    shuffle_indexes=np.random.permutation(len(data))
    init_centers = shuffle_indexes[:n]  # 对应的是选择的初始中心样本的id（随机选择）
    data_, label_, center, rounds  = kmeans(data, init_centers)  # 得到K-Means聚类的结果
    evaluate_res = metrics.silhouette_score( data_, label_)
    print("共%d簇 Silhouette Coefficient: %0.3f" %(n,  evaluate_res)) # 轮廓系数，越大聚类效果越好
    best_k.append((evaluate_res, n, data_, label_, center))

best_k = sorted(best_k, key=lambda x: x[0])[-1] # 选择聚类效果最好的k作为最终的聚类结果

fig, ax = plt.subplots(1, 1, figsize=(5, 5))
ax.set_xlim(0, 1)
ax.set_ylim(0, 0.6)
ax.set_ylabel('sugar')
ax.set_xlabel('density')
colors = np.array(["red", "gray", "orange", "pink", "blue", "black"])
silhouette_score, n, data_, label_, center = best_k
print("Silhouette Coefficient: %0.3f" % metrics.silhouette_score(data_, label_)) # 轮廓系数，越大聚类效果越好
plt.scatter(data_[:, 0], data_[:, 1], c=colors[label_], s=100)
plt.show()