算法题目
水仙花数(Narcissistic number)也被称为超完全数字不变数(pluperfect digital invariant, PPDI)、自恋数、自幂数、阿姆斯壮数或阿姆斯特朗数(Armstrong number),水仙花数是指一个 3 位数,它的每个位上的数字的 3次幂之和等于它本身。例如:1^3 + 5^3+ 3^3 = 153。
水仙花数只是自幂数的一种,严格来说3位数的3次幂数才称为水仙花数。
--- 引自百度百科
自幂数是指一个 n 位数,它的每个位上的数字的 n 次幂之和等于它本身
算法思路
参数:n : n位数,每个数字的n次幂
1,预先计算1~9 的 n次幂,放入map备用
2,预先计算 10 的 0~n 次幂,放入map备用
2,n位数最小值,最大值,遍历升次对比
3,将符合条件的放入列表
代码实现
/**
* 求 自幂数
* @param n 位数
* @return
* @throws Exception
*/
public static List<Integer> sxhGet(int n) throws Exception{
// int的取值范围为:-2^31 ---- 2^31-1 ,即:-2147483648 - 2147483647
if(n > 10){
throw new Exception("no support");
}
// +1
List<Integer> ret = new ArrayList<>();
// +1
HashMap<Integer,Integer> map = new HashMap<>();
//10 的 0~n 次幂
HashMap<Integer,Integer> powMap = new HashMap<>();
for(int i=1;i<=n;i++){
powMap.put(i,(int)Math.pow(10,i-1));
}
// +10
for(int i=0;i<10;i++){
map.put(i,(int)Math.pow(i,n));
}
//最大值 +1
int max = (int)Math.pow(10,n) -1;
//最小值 +1
int min = (int)Math.pow(10,n-1);
// 10^(n) - 10^(n-1) -1
for(int i = min;i<max+1;i++){
// 各位三次幂和存储 +1
int sum = 0;
// 临时位数 +1
int s = n;
int si = i;
// 5(n-1)
while (s > 0 && si>0 ){
int powi = powMap.get(s);
int temp = si/powi;
sum += map.get(temp);
s--;
si = si-temp*powi;
}
if(i == sum){
ret.add(i);
}
}
return ret;
}
接下来需要考虑的问题
1,算法是否正确
2,算法复杂度如何
3,算法是否需要优化
算法是否正确
1位自幂数:[1]
2位自幂数:[]
3位自幂数:[153, 370, 371, 407]
4位自幂数:[1634, 8208, 9474]
5位自幂数:[54748, 92727, 93084]
6位自幂数:[548834]
7位自幂数:[1741725, 4210818, 9800817, 9926315]
8位自幂数:[24678050, 24678051, 88593477]
9位自幂数:[146511208, 472335975, 534494836, 912985153]结果验证无误,说明算法思路没有问题。
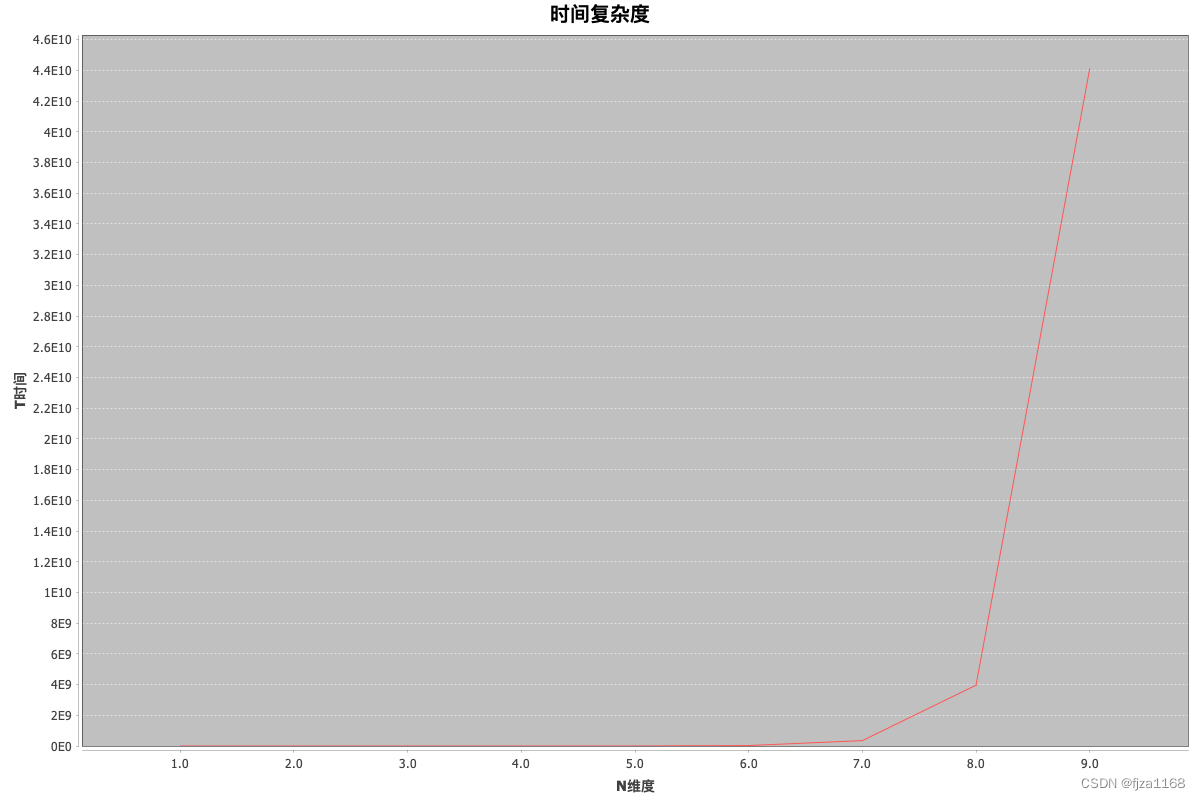
算法复杂度
时间复杂度:15+n+(9 * 10^(n-1) -1) * (4+5n)
指数级时间复杂度,遇到指数级炸弹
是否需要优化
8位用5秒,9位用50秒,按目前int位来说还可忍受, 按百度百科给出的最大位数39,该算法不可能达到,算法需要重构优化
目前对优化还没有思路,待研究透彻再补充,如果有思路的欢迎留音讨论