目录

排序思想：

演示图：

代码实现

总结：

---

排序思想：

· 在元素集合 array[i]--array[n-1] 中选择关键码最大 ( 小 ) 的数据元素

· 若它不是这组元素中的最后一个 ( 第一个 )元素，则将它与这组元素中的最后一个（第一个）    元素交换

· 在剩余的 array[i]--array[n-2] （ array[i+1]--array[n-1] ）集合中，重复上述步骤，直到集合剩余 1 个元素

演示图：

  

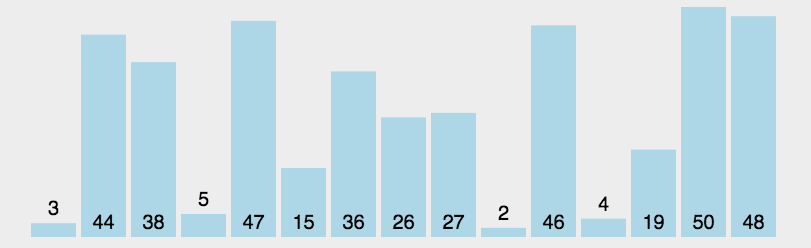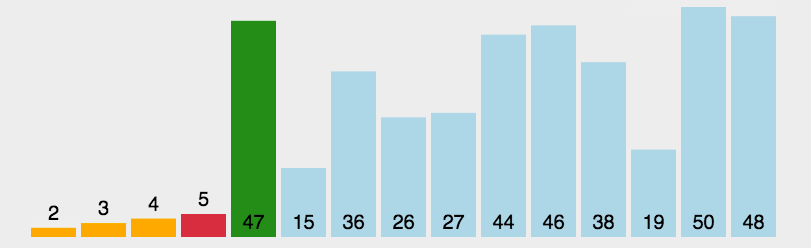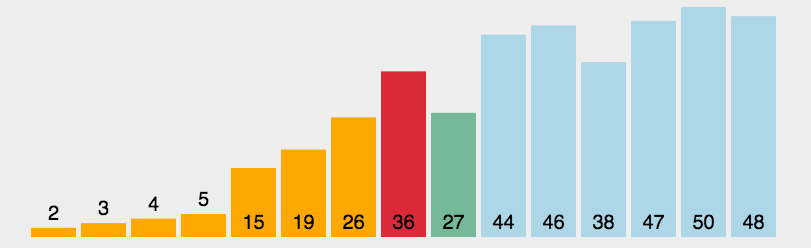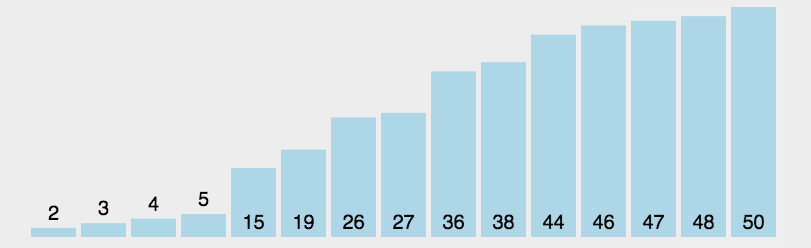
代码实现

单趟思路：

设置四个 int 类型数据 mini 、maxi 、begin、end 记录这一趟中所遇到的最小值与最大值以及开头和结尾的下标。遍历一遍找到所对应的值，交换 mini 和 begin  以及 maxi 和 end 对应的数据的值。

分析：如果第一个是最大值是在begin的位置，在 mini 和 begin 交换时被换走之后但是maxi仍然指向怎么办？

很简单，我们只需要做出以下操作，将maxi改正到指向正确的值上即可。

if (maxi == begin)
{
	maxi = mini;
}

代码：

int begin = 0, end = n - 1;
	int mini = begin, maxi = begin;
	for (int i = begin + 1; i <= end; ++i)
	{
		if (a[i] > a[maxi])
		{
			maxi = i;
		}
		if (a[i] < a[mini])
		{
			mini = i;
		}
	}
	Swap(&a[mini], &a[begin]);

	//避免了如果第一个数最大,会被换走,但是maxi还指向第一个数
	if (maxi == begin)
	{
		maxi = mini;
	}
	Swap(&a[maxi], &a[end]);
	++begin;
	--end;

整轮实现：加上循环即可，我们只需要让 begin < end 的时候进行循环就可以走完整轮了。

代码：

void SelectSort(int* a, int n)
{
	int begin = 0, end = n - 1;
	while (begin < end)
	{
		int mini = begin, maxi = begin;
		for (int i = begin + 1; i <= end; ++i)
		{
			if (a[i] > a[maxi])
			{
				maxi = i;
			}
			if (a[i] < a[mini])
			{
				mini = i;
			}
		}
		Swap(&a[mini], &a[begin]);

		//避免了如果第一个数最大,会被换走,但是maxi还指向第一个数
		if (maxi == begin)
		{
			maxi = mini;
		}
		Swap(&a[maxi], &a[end]);
		++begin;
		--end;
	}
}

  

总结：