前言:上一篇我们讲了二叉树,你知道吗?堆的底层是一棵完全二叉树。这样说会不会就会觉得熟悉了。
目录
1.堆的概念及存储方式
2:堆的创建
2.1:向下调整
3.堆的插入和删除
3.1:堆的插入
3.2:堆的删除
4.PriorityQueue的特性-----优先级队列
4.1常用接口介绍
4.1.1:优先级队列的构造
4.1.2:插入/删除/获取
5:应用
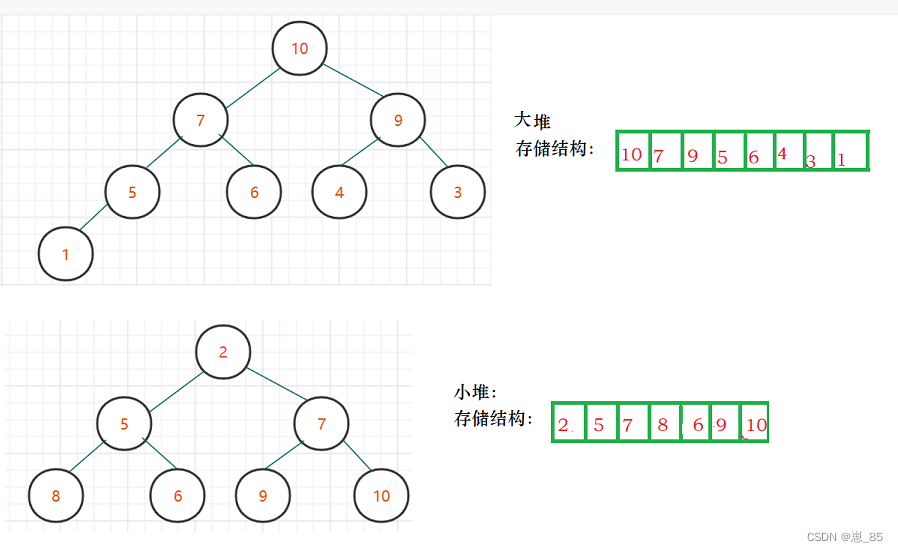
1.堆的概念及存储方式
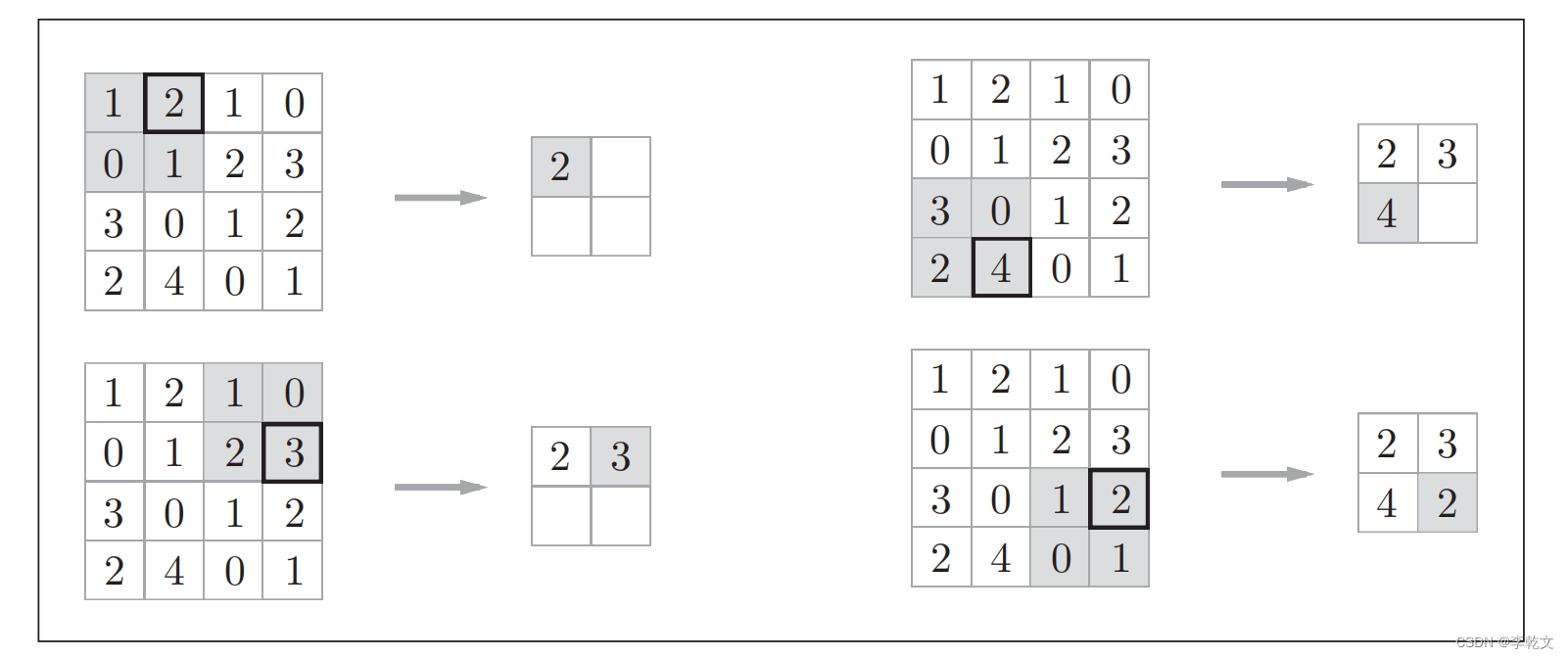
它的所有元素按照完全二叉树的顺序存储方式存储在一个一维数组中。
如果i为0,表示根节点。否则父亲节点:(i-1)/2
如果i*2+1小于节点个数。左孩子:2*i+1
如果i*2+2小于节点个数。右孩子:2*i+2
大堆:根节点比左右孩子都大。
小堆:根节点比左右孩子都小。
存储方式:堆是一颗完全二叉树,因此可以层序的规则采用顺序的方式来高效存储。
2:堆的创建
public class MyHeap {
//它的存储结构是一维数组
public int [] elem;
public int usedSize;//记录数组中的有效元素个数
public static final int DEFIND_SIZE=10;//数组容量
//开辟数组空间
public void createHeap(){
elem=new int [DEFIND_SIZE];
}
2.1:向下调整
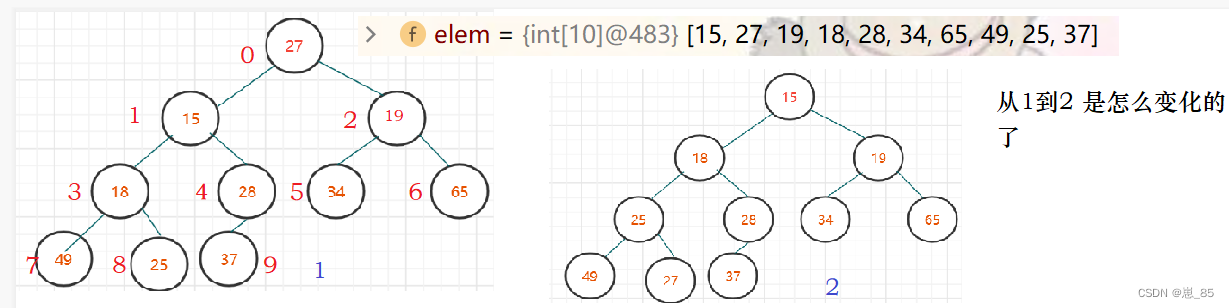

public void CreateMinHeap(){
for (int parent =(usedSize-1)/2 ; parent>=0; parent--) {
shiftDown(parent,usedSize);//向下调整
}
}
public void shiftDown(int parent,int len){
int child=parent*2+1;
//必须有左孩子
while(child<len){
//判断它是否有右孩子,看谁的值比较小
if(child+1<len&&elem[child+1]<elem[child]){
child++;//child是最小的
}//判断父亲节点和孩子节点那个小
if(elem[parent]>elem[child]){//大于就交换
swap(elem,parent,child);
parent=child;
child=parent*2+1;
}else{//不大于
break;
}
}
}
public void swap(int [] elem,int i,int j){
int tmp=elem[i];
elem[i]=elem[j];
elem[j]=tmp;
}
}3.堆的插入和删除
3.1:堆的插入
堆的插入总共需要两个步骤
1.判断空间够不够,够就将元素放到底层空间中;不够,扩容
2.将最后新插的节点向上调整,知道堆的性质。

//堆的插入
public void offer(int val){
//判断空间是否够
if (isFull()){
//满了,扩容
//以二倍扩容
elem= Arrays.copyOf(elem,elem.length*2);
}//没有满
elem[usedSize]=val;
shiftUp(usedSize);
usedSize++;//记录有效元素个数加加
}
//向上调整
public void shiftUp(int child){
//找到它的父亲
int parent=(child-1)/2;
while(parent>=0){
if(elem[parent]>elem[child]){
swap(elem,parent,child);
child=parent;
parent=(child-1)/2;
}else{
break;
}
}
}
public boolean isFull(){
//如果有效元素个数等于大于数组长度
//说明数组满了
return usedSize>=elem.length;
}
}3.2:堆的删除
注意:堆的删除一定时堆顶元素
1.将最后一个元素和堆顶元素交换。
2.将有效元素个数减减。
3.向下调整,符合堆的性质
public int pop(){
//判断堆是否为空
if(isEmpty()){
return -1;
}//不为空,和最后一个元素交换位置
int tmp=elem[0];
swap(elem,0,usedSize-1);
//有效元素减
//向下调整
shiftDown(0,usedSize-1);
return tmp;
}4.PriorityQueue的特性-----优先级队列
优先级队列的底层是堆。
注意事项:
1.PriorueueQueue中放置的元素必须是能够比较大小,否则会抛出ClassCastException异常。
2.不能插入null对象.否则会抛出NullpointerException
3.没有容量限制,可以插入任意元素。
4.PriorityQueue默认情况是小堆
4.1常用接口介绍
4.1.1:优先级队列的构造
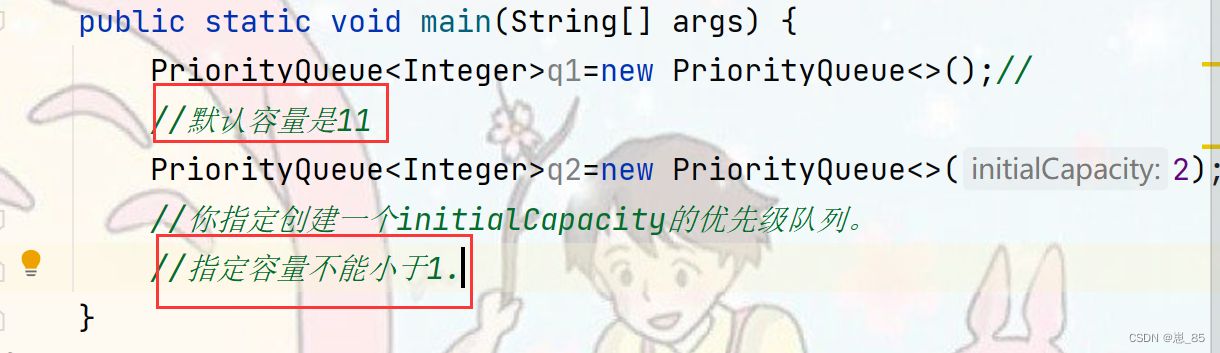
4.1.2:插入/删除/获取
| 函数名 | 功能介绍 |
| boolean offer(E e) | 插入e,成功返回true. |
| E peek() | 获取优先级最高的元素,如果为空,返回null |
| int size() | 获取有效元素个数 |
| E poll() | 移除优先级最高的元素并返回,如果为空,返回null |
| void clear() | 清空 |
| boolean isEmpty() | 检查优先级队列是否为空,空返回null |
扩容说明:
如果容量小于64是按照2倍方式扩容
如果容量大于64是按1.5倍方式扩容
如果容量大于最大值,按照最大值来进行扩容
5:应用
5.1:Top-k问题
1.用数据集合中前K个元素来建堆
1.1:前K个最大的元素,建小堆
1.2:前k个最小的元素,建大堆。
2。用剩下的元素依次和堆顶元素来比较,不满足则替换堆顶元素。
https://leetcode.cn/problems/smallest-k-lcci/
class Solution {
public int[] smallestK(int[] arr, int k){
//判断k是否大于1,数组是否为空
if(arr.length==0||k<1){
return new int[0];
}
PriorityQueue<Integer> p1=new PriorityQueue<>
(k, new Comparator<Integer>() {
@Override
public int compare(Integer o1, Integer o2) {
return o2-o1;
}
});
//将前k个元素,建成大堆
for (int i = 0; i <k ; i++) {
p1.offer(arr[i]);
}
//把剩下的元素和堆顶元素相比
for (int i = k; i <arr.length ; i++) {
int tmp = p1.peek();
if (tmp >arr[i]) {
p1.poll();
p1.offer(arr[i]);
}
}
//将堆的元素赋值到数组里
int [] ret=new int[k];
for (int i = 0; i <k ; i++) {
ret[i]= p1.poll();
}
return ret;
}
}总结;
以上就是我总结的堆的知识点。若有错误,请各位铁铁留言纠错。若感觉不错,请一键三连。