数据结构之：链表

链表初体验之单链表

线性表

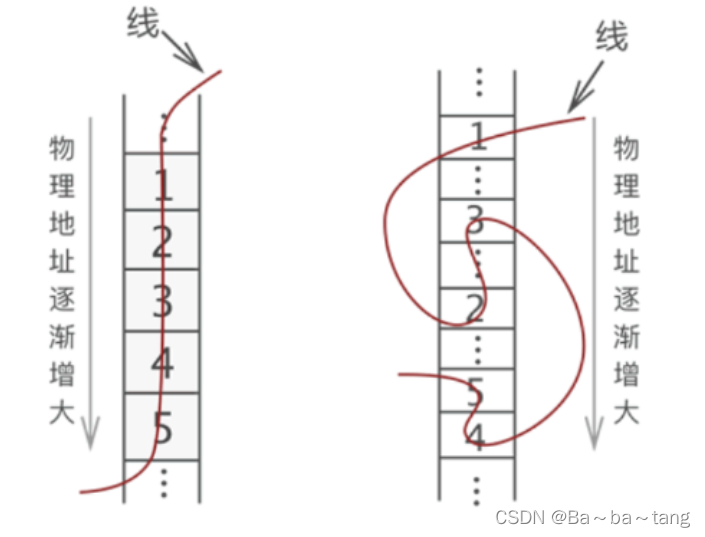
线性表 " 线性存储结构 " —— 一根线能串起来的数组存储到物理空间之中

数据需要有相同的数据类型

元素之间的关系需要是 “ 一对一 ”

两种存储方式 “ 顺序 ” 和 “ 链式 ”

链表介绍

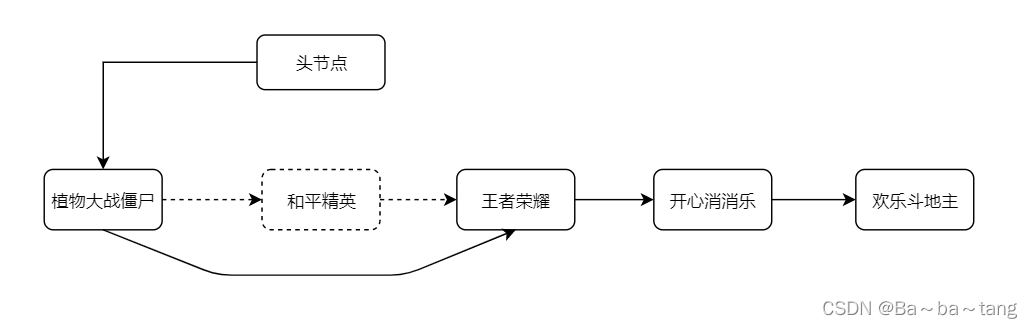
分为有头节点的链表和没有头节点的链表。

插入的时候，分为头插法和尾插法。

节点的关系，称之为前置节点和后继节点。

节点的构成，包含数据本身，以及对后继节点的引用。

单链表之倒数第 k 个节点

链表中倒数第 k 个节点

https://leetcode-cn.com/problems/lian-biao-zhong-dao-shu-di-kge-jie-dian-lcof/

链表中倒数第 k 个节点

输入一个链表，输出该链表中倒数第 k 个节点。为了符合大多数人的习惯，本题从 1 开始计数，即

链表的尾节点是倒数第 1 个节点。例如，一个链表有 6 个节点，从头节点开始，它们的值依次是

1 、 2 、 3 、 4 、 5 、 6 。这个链表的倒数第 3 个节点是值为 4 的节点。

示例：

给定一个链表 : 1->2->3->4->5, 和 k = 2.

返回链表 4->5

分析：

解法1 ）

先遍历出链表的总长度 n 倒数第 k 个节点 = 从头遍历的第 n-k+1 个节点

    public static ListNode getKthFromEnd(ListNode head, int k) {
        int n = 0;
// 先求出链表总长度
        ListNode tmp = head;
        while (tmp.next != null) {
            n++;
            tmp = tmp.next;
        }
// 再次遍历 找到第n-k+1个节点
        tmp = head;
        for (int i = 0; i < n - k + 1; i++) {
            tmp = tmp.next;
        }
        return tmp;
    }

解法2：

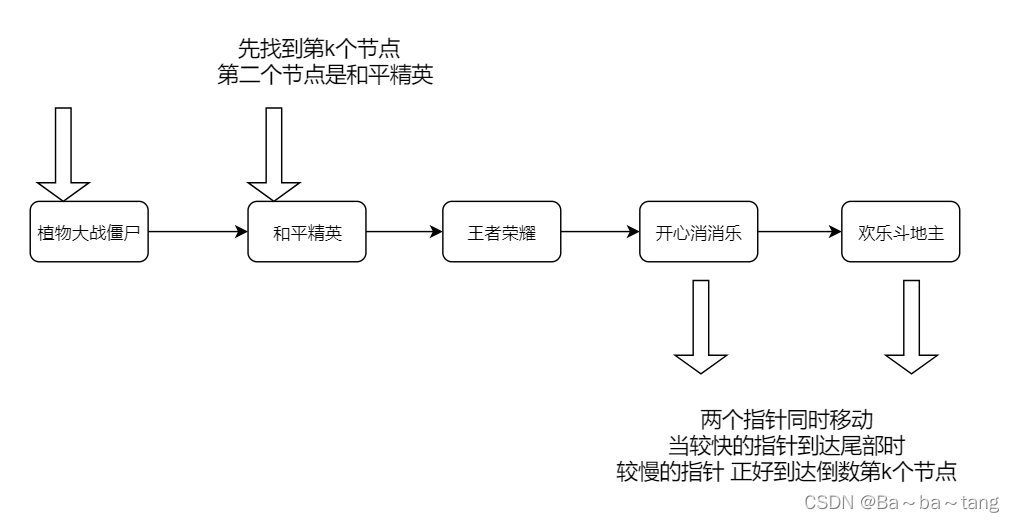
先定义额外指针找到正数第 k 个节点

两个指针同时向后移动当快的指针到达链表最后一个节点时

慢的指针正好到达倒数第 k 个节点

( 相当于慢的指针没走的 k 步由快的指针帮忙走完了 )

    public static ListNode getKthFromEnd1(ListNode head, int k) {
// 快慢指针
        ListNode slow = head;
        ListNode fast = head;
// 正数第k个节点
        for (int i = 1; i < k; i++) {
            fast = fast.next;
        }
        System.out.println(fast.val);
        while (fast.next != null) {
            slow = slow.next;
            fast = fast.next;
            System.out.println("slow移动到" + slow.val + ",fast移动到" +
                    fast.val);
        }
        return slow;
    }

单链表之反转链表

反转链表

https://leetcode-cn.com/problems/reverse-linked-list/

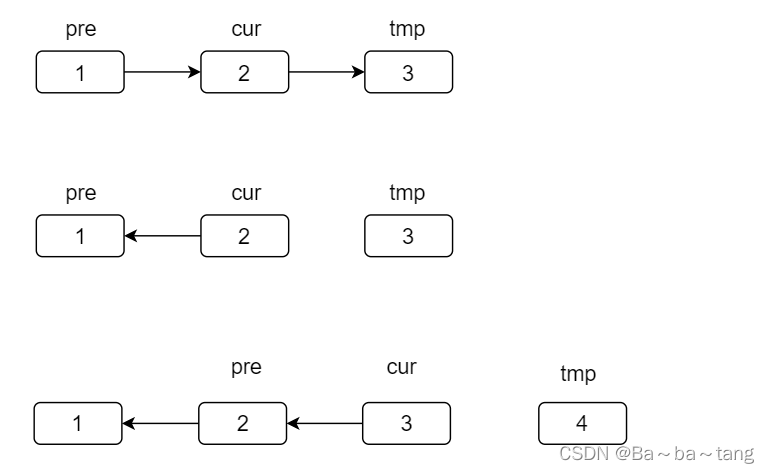
反转链表

反转一个单链表。

示例 :

输入 : 1->2->3->4->5->NULL

输出 : 5->4->3->2->1->NULL

进阶 :

你可以迭代或递归地反转链表。你能否用两种方法解决这道题？

迭代的方法分析：

让一个节点的 next 指向前置节点 (2->1)

让原 next 节点指向自身 (3->2)

也就是，记录前置节点，变更指向

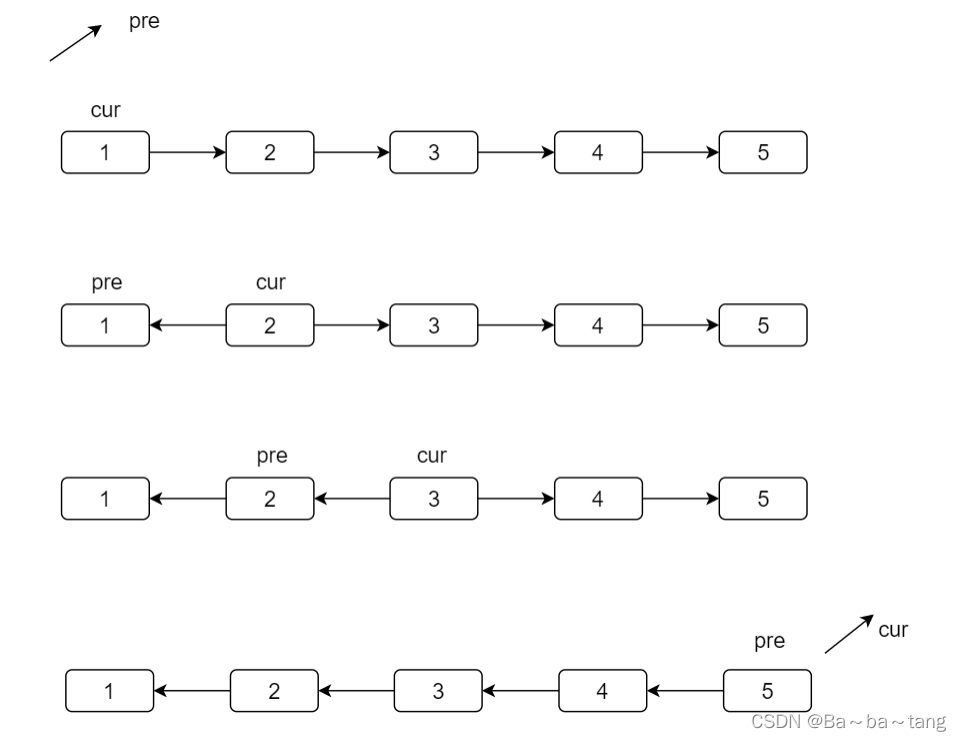
每一次迭代的操作分析

在引用更改时，会丢失原 next 节点的引用，需要用临时指针 tmp 记录一下

    public static ListNode reverseList(ListNode head) {
// 记录前置节点 和当前节点
        ListNode pre = null;
        ListNode cur = head;
// 不断移动cur节点 向后遍历 同时更改其next
// 当cur 为空时 遍历完成
        while (cur != null) {
            ListNode tmp = cur.next;
// 更改指向
            cur.next = pre;
            if (cur != null && pre != null) {
                System.out.println("让" + cur.val + "的next指向" + pre.val);
            }
// pre和cur向后移动
            pre = cur;
            cur = tmp;
        }
        return pre;
    }

双链表的那些事儿

双链表

1 ）链表和数组的区别

优点，链表实现了真正的动态，不需要处理固定容量带来的系列问题

缺点，失去随机访问的能力

链表增删快，查询慢；数组查询快，增删慢。

2 ）结构

单链表数据 + 下一个节点的引用

双链表

数据 + 下一个节点的引用 + 对上一个节点的引用

数据 + 后置指针 + 前置指针

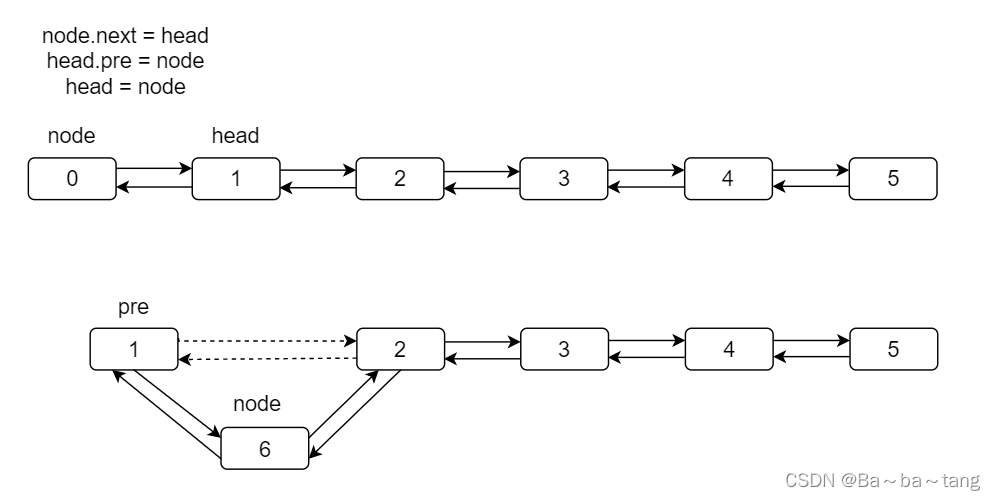
添加元素

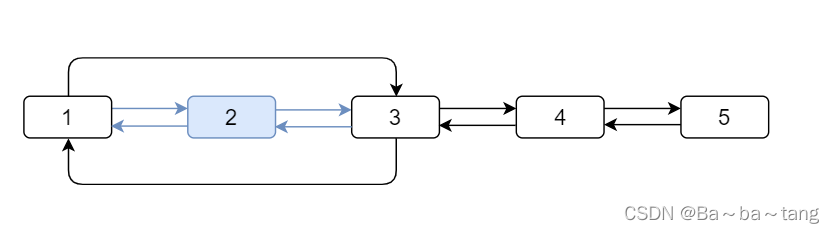
删除元素

java 的经典实现 —— LinkedList

查询方式

如根据元素索引位置找到元素

如果索引在前半段，从头往后遍历；如果索引在后半段，从后往前遍历。

环形链表的兜兜转转

环形链表

给链表加环的逻辑

    // pos 代表 尾节点指向 链表中某个节点的索引位置 (环的入口)
    public static void toCycle(ListNode node, int pos) {
// 遍历 通过pos找到 入口对应的节点 记录下来
// 遍历到尾节点时 设置为其next引用
// 记录遍历的位置
        int cnt = 0;
        ListNode cycleNode = null;
        while (true) {
// 判断是否是环的入口节点
            if (cnt == pos) {
                cycleNode = node;
            }
// 判断是否是尾节点
            if (node.next == null) {
                node.next = cycleNode;
                return;
            }
            node = node.next;
            cnt++;
        }
    }

1 ）判断是否有环

https://leetcode-cn.com/problems/linked-list-cycle/

141. 环形链表

给定一个链表，判断链表中是否有环。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。为了表示给

定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果

pos 是 -1 ，则在该链表中没有环。注意： pos 不作为参数进行传递，仅仅是为了标识链表的实际

情况。

如果链表中存在环，则返回 true 。否则，返回 false 。

进阶：

你能用 O(1) （即，常量）内存解决此问题吗？

示例 1 ：

输入： head = [3,2,0,-4], pos = 1

输出： true

解释：链表中有一个环，其尾部连接到第二个节点。

示例 2 ：

输入： head = [1,2], pos = 0

输出： true

解释：链表中有一个环，其尾部连接到第一个节点。

示例 3 ：

输入： head = [1], pos = -1

输出： false

解释：链表中没有环。

分析：

环形链表其实是形成了一个圈

跑步时快的人和慢的人在某一点相遇这能倒推出跑道是环形的

“ 快慢指针 ” 构造一个遍历时走一步的指针为慢指针

走两步的指针为快指针如果两者在某节点相遇可以断定链表为环形

   public static boolean hasCycle(ListNode head) {
// 链表本身不能为空 或者只有一个节点 也是无环的
        if (head == null || head.next == null) {
            return false;
        }
        ListNode slow = head;
        ListNode fast = head;
        while (true) {
// 没有环时 fast会先走到链表尾部
            if (fast == null || fast.next == null) {
                return false;
            }
            slow = slow.next;
            fast = fast.next.next;
            if(slow != null) {
                System.out.print("slow走到" + slow.val);
            }
            if(fast != null) {
                System.out.println(",fast走到" + fast.val);
            }
            if (slow == fast) return true;
        }
    }

2) 求环的入口节点

https://leetcode-cn.com/problems/linked-list-cycle-ii/

142. 环形链表 II

给定一个链表，返回链表开始入环的第一个节点。如果链表无环，则返回 null 。

为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开

始）。如果 pos 是 -1 ，则在该链表中没有环。

说明：不允许修改给定的链表。

示例 1 ：

输入： head = [3,2,0,-4], pos = 1

输出： tail connects to node index 1

解释：链表中有一个环，其尾部连接到第二个节点。

分析：

“ 快慢指针 ” 第一次相遇后，让 fast 重新指向头结点 head,slow 保持不变。

fast 和 slow 按照相同速度移动，第二次相遇后，此节点即为入口节点。

[3,2,0,-4]

slow 3 2 0 -4 走了三步

fast 3 0 2 -4 走了六步（是 slow 的 2 倍）

fast - slow 的步数其实是环的长度 6-3=3

相遇点为 -4 ，距离环的入口节点步数为两步

（指的是入口节点通往相遇点的方向距离 2->0->-4 ）

因为头结点途经的路程是从头结点出发经过入口节点到达相遇点的

头结点到入口节点的距离为一步

因为环的长度已知

所以从相遇点再行进多少步能回到入口节点 = 环的长度 - 相遇点距离入口节点的步数

slow -4 2

fast 3 2

    public static ListNode detectCycle(ListNode head) {
// 链表本身不能为空 或者只有一个节点 也是无环的
        if (head == null || head.next == null) {
            return null;
        }
        ListNode slow = head;
        ListNode fast = head;
        while (true) {
// 没有环时 fast会先走到链表尾部
            if (fast == null || fast.next == null) {
                return null;
            }
            slow = slow.next;
            fast = fast.next.next;
            if(slow != null) {
                System.out.print("slow走到" + slow.val);
            }
            if(fast != null) {
                System.out.println(",fast走到" + fast.val);
            }
            if (slow == fast) break;
        }
// 第一次相遇后，让fast重新指向头结点head,slow保持不变。
// fast和slow按照相同速度移动，第二次相遇后，此节点即为入口节点。
        fast = head;
        while (true){
            slow = slow.next;
            fast = fast.next;
            if(slow != null) {
                System.out.print("slow走到" + slow.val);
            }
            if(fast != null) {
                System.out.println(",fast走到" + fast.val);
            }
            if(slow == fast) return slow;
        }
    }

经典应用之约瑟夫环问题

约瑟夫环

有 N 个人围成一圈，从第一个人开始报数，报到 M 被杀，然后下一个人继续从 1 开始报数，循环往复，直

到剩最后一个，最后一个人的初始位置在哪里？

f(n,m)

f(3,3) -> 1

0 1 2

A B C1

A2 B

f(4,3) -> 0

0 1 2 3

A B C1 D

D A B2

D3 A

分析：

A ）环形链表法

将每个人视作链表中的一个节点，当报数到 m 的时候，删除节点，直到剩下最后一个节点

当找到报数 m-1 的节点 node node.next = node.next.next

当只剩最后一个节点时 node.next = node

    public static int josephus(int n, int m) {
// 初始化环形链表
        int[] arr = new int[n];
        for (int i = 0; i < arr.length; i++) {
            arr[i] = i + 1;
        }
        ListNode node = ListNode.arrayToListNode(arr);
        ListNode.toCycle(node, 0);
// 将每个人视作链表中的一个节点，当报数到m的时候，删除节点，直到剩下最后一个节点
// 当找到报数m-1的节点 node node.next = node.next.next
// 当只剩最后一个节点时 node.next = node
        int cnt = 1;
        while (true) {
            if (cnt == m - 1) {
                System.out.println("删除节点" + node.next.val);
                node.next = node.next.next;
                cnt = 0;
            }
            node = node.next;
            cnt++;
            if (node.next == node) return node.val;
        }
    }

B ）数组遍历法

将每个人视作数组中的一个元素，当报数到 m 的时候，使用占位符代表此人死掉了

当剩余人数只有一人时停止循环

    public static int josephus1(int n, int m) {
// 数组记录 初始值是0 使用-1代表当前元素 死掉
        int[] people = new int[n];
// 人的索引
        int index = -1;
// 报数 1 2 ... m
        int cnt = 0;
// 剩余人数
        int remain = n;
        while (remain > 0) {
            index++;
// 到达数组末端 重新从头遍历
            if (index >= n) index = 0;
// 如果此人死掉 跳过 继续报数
            if (people[index] == -1) {
                continue;
            }
// 报数到m 将index对应位置的元素 置为-1 (尸体)
            if (cnt == m) {
                people[index] = -1;
                cnt = 0;
                remain--;
            }
            cnt++;
        }
        return index;
    }