大纲
- 引言
- 回归问题中的长尾分布
- LDS
- FDS
- 实验和结果
- 总结
引言
本文是长尾分布系列论文解析的第二篇,前情提要详见长尾分布系列论文解析(一)Decoupling Representation and Classifier for Long-Tailed Recognition,本篇要介绍的是回归任务中的长尾分布问题,相关论文为:
- Delving into Deep Imbalanced Regression
回归问题中的长尾分布
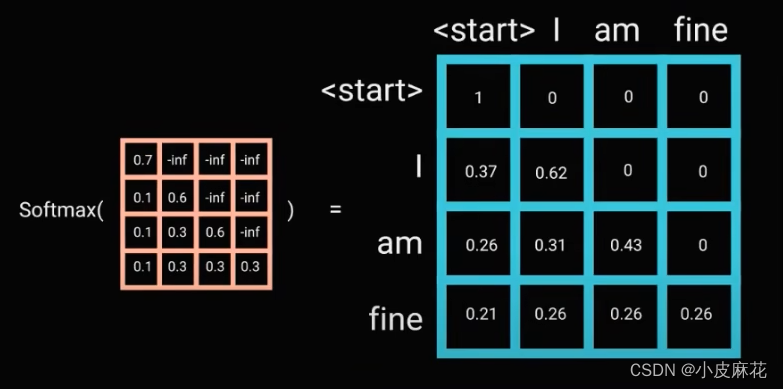
回归问题中的长尾分布和分类问题中的长尾分布存在着显著的区别,在回归问题中某一类(区间)的样本数目并不是仅仅只和其本身有关,而是和其邻域范围内的样本数目也有着关系。这是因为回归问题中的不同类别或者说是区间是存在着相似性的概念,相邻类别的样本是可以存在一定程度的信息共享和知识迁移的,即使是本类样本数目偏少,但在领域样本数目多的情况下也能获得不错的预测效果。而在分类问题中,不同类别样本的共享特征则少之又少。因此,可以总结成一句话:回归问题中的长尾分布并不能反应训练过程中模型看到的数据分布,作者也从实验的角度对这一结论进行了验证,分别检验了分类问题和回归问题中的数据分布与误差分布的关系:

可以看出在分类问题中测试集上的误差和训练数据分布基本出互补的趋势,即样本越多误差越小;而在回归问题中,这一趋势则没有明显体现,不同类样本的误差和训练数据数目的负相关性远不如分类问题中的来的强。
针对回归(连续标签预测)问题中长尾分布的特性,作者设计了LDS(Label Distribution Smoothing)和FDS(Feature Distribution Smoothing)两种方案来拟合其真实分布,从而可以将经典的长尾分布解决方法迁移到回归问题上。
LDS
LDS从标签的角度对回归问题中的数据分布进行平滑,具体而言就是用对称的核函数对数据集的原始标签分布进行滤波,从而使得每一类样本的出现概率都不仅仅与其本身有关,还牵涉到了领域样本的出现概率。典型的对称核函数有
高斯核或者拉普拉斯核。LDS使用后的效果如下图所示:

FDS
FDS从特征的角度对数据分布进行平滑,背后的基础假设是如果样本在标签的分布上具有连续性,那么在特征空间的分布同样应该具有连续性,也就意味着标签域上临近的样本在特征域上也应该更相近,反之亦然。而实际实验中的结果却并不如预先的一般,如下图:

可以看到在以某类多数样本的特征矩阵作为锚点和其他类比进行相似性度量时,其临近的多数样本和锚点具有很高的相似性,这证明了猜想是有一定道理的。但远处的少数样本类别同样有着较高的、反常相似性,这是因为其样本数目过少,模型无法从中学到足够的知识,而是暴力的将多数样本的信息迁移到其上,导致学到的特征非常类似。
为了解决这一问题,作者提出了FDS以在特征域上进行平滑,实现领域的特征共享。具体而言,首先对于给定的类别,首先计算其类内特征的均值和协方差如下:
μ
=
1
N
b
∑
i
=
1
N
b
z
i
Σ
b
=
1
N
b
−
1
∑
i
=
1
N
b
(
z
i
−
μ
b
)
(
z
i
−
μ
b
)
T
\mu=\frac{1}{N_b}\sum_{i=1}^{N_b}z_i\\ {\varSigma_b}=\frac{1}{N_b-1}\sum_{i=1}^{N_b}(z_i-\mu_b)(z_i-\mu_b)^T
μ=Nb1i=1∑NbziΣb=Nb−11i=1∑Nb(zi−μb)(zi−μb)T
其中
μ
b
\mu_b
μb为第
b
b
b类样本的容量。而后和LDS一般利用对称核对类别特征向量的均值和方差进行平滑如下:
μ
b
~
=
∑
b
′
∈
B
k
(
y
b
,
y
b
′
)
μ
b
′
Σ
b
~
=
∑
b
′
∈
B
k
(
y
b
,
y
b
′
)
Σ
b
′
\tilde{\mu_b}=\sum_{b'\in B}k(y_b,y_b')\mu_{b'}\\ \tilde{\varSigma_b}=\sum_{b'\in B}k(y_b,y_b'){\varSigma_b'}
μb~=b′∈B∑k(yb,yb′)μb′Σb~=b′∈B∑k(yb,yb′)Σb′
最后利用平滑之后的均值和方差对类内的每个样本进行whitening和re-coloring操作(这一操作其实是用于域迁移的,将特征从原始的域迁移到平滑域),以聚合周围类别样本的特征信息:
z
~
=
Σ
~
b
1
2
Σ
b
−
1
2
(
z
−
μ
0
)
+
μ
~
b
\tilde{z}=\tilde{\varSigma}_b^{\frac{1}{2}}\varSigma_b^{-\frac{1}{2}}(z-\mu_0)+\tilde{\mu}_b
z~=Σ~b21Σb−21(z−μ0)+μ~b
而这一特征空间的平滑过程也用到了动量更新的思路以保证训练的稳定,在当前epoch内对所有的mini-batch都使用前一轮次的平滑后均值、方差进行重校准,每个mini-batch训练完成在类内进行带动量的均值和方差更新,当前epoch计算完成后对累计的均值、方差进行平滑,实际流程如下:

实验和结果
FDS和LDS的优越之处在于可以嵌入到现有的长尾分布解决方案当中,以适应回归问题。作者将二者和多种方法如基于损失函数加权的方法,基于数据重采样方法,解耦方法等等相结合,大部分情况下都能有效提高模型的表现。更进一步的,FDS和LDS可以增强模型的zero-shot泛化能力,即使是在训练集中为出现的类别样本,测试时也因获得了邻域信息而可以得到不错的预测。(但实际上这些相对提升都没有特别大,可能这个领域本身就在瓶颈)
FDS的效果和原理也得到了实验的支撑,将少数类别样本的特征作为锚点时,使用FDS前后和其他类样本的特征相似性发生了显著的变化,更加符合预期。

总结
这篇论文的motivation和解决措施都十分的漂亮,实验做的也很充分,非常solid,作者原解析:ICML 2021 (Long Oral) | 深入研究不平衡回归问题,源代码:imbalanced-regression