1、选择排序

首先在未排序数列中找到最小元素，然后将其与数列的首部元素进行交换，然后，在剩余未排序元素中继续找出最小元素，将其与已排序数列的末尾位置元素交换。以此类推，直至所有元素均排序完毕.复杂度为n2，复杂度还是相当高的

选择排序即是采用交换次数最少的方针进行排序，选择排序的交换次数要远远少于冒泡排序

力扣2471逐层排序二叉树所需的最少操作数目用到了选择排序算法

选择排序算法是不稳定的，值相同的元素的相对位置可能会发生改变，这一点需要特别注意

 2、快速排序

快速排序是不稳定的

快速排序的时间复杂度在最坏情况下是O(N2)，平均的时间复杂度是O(N*lgN)。

 详细思路见常见几种java排序算法_zzzgd816的博客-CSDN博客

代码及注解如下所示

public void sort(int arr[],int begin,int end){
        if(begin>=end){
            return;
        }
        //左边的i，左指针
        int start_pos=begin;
        //右边的j，右指针
        int end_pos=end;
        //基准值，默认为第一个元素
        int standard=arr[start_pos];
        while (start_pos<end_pos){
            //右指针开始往左移，寻找比基准值小的元素
            while (start_pos<end_pos&&standard<=arr[end_pos]){
                end_pos--;
            }
            //如果确实找到该元素，那么就进行置换，置换过后左指针右移一位
            if(arr[end_pos]<standard){
                arr[start_pos]=arr[end_pos];
                start_pos++;
            }
            //左指针开始往右移动，寻找比基准值大的元素
            while (start_pos<end_pos&&standard>=arr[start_pos]){
                start_pos++;
            }
            //如果确实找到该元素，那么就进行置换，置换过后右指针左移一位
            if(arr[start_pos]>standard){
                arr[end_pos]=arr[start_pos];
                end_pos--;
            }
        }
        //左右指针重叠，将基准值赋予左右指针重叠处
        arr[start_pos]=standard;
        //分治递归
        sort(arr,begin,start_pos-1);
        sort(arr,start_pos+1,end);
 }

3、堆排序

什么是堆？

 堆的实现方式： 

数组按顺序存储层序遍历的二叉树，按顺序全部放进来，因为是完全二叉树，数组中间不可能存在空缺

 用数组存储这样的好处便是，已知一个节点在数组中的索引为k时，它的父节点位置为k/2，它的两个子结点的位置分别为2k和2k+1.如此这般，在不使用指针的情况下，也可以通过计算数组的索引在树中上下移动，从a[k]向上一层，就令k=k/2，向下一层就令k等于2k或2k+1

堆的特性：

对于每个节点的值都大于等于子树中每个节点值的堆，我们叫做“大顶堆”。对于每个节点的值都小于等于子树中每个节点值的堆，我们叫做“小顶堆”。

堆的插入：

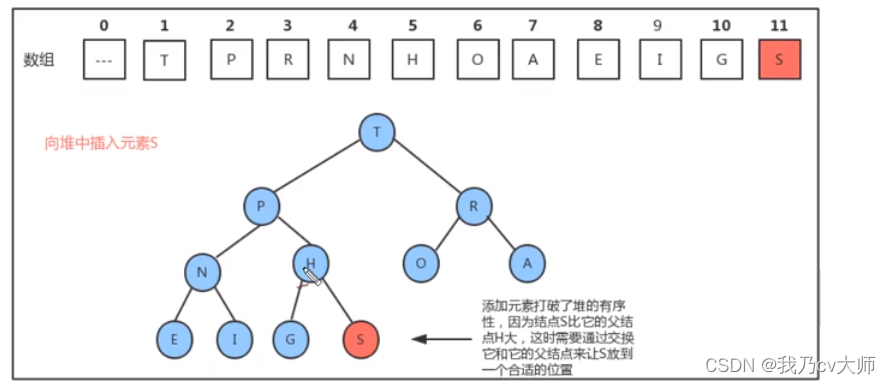
 插入新节点s，插入节点后，堆不一定还是标准的堆，需要将插入的元素不断向父节点的值去做比较，如果不符合条件，则交换两者的值，直到父节点的值与子节点的关系符合条件为止，如图所示：

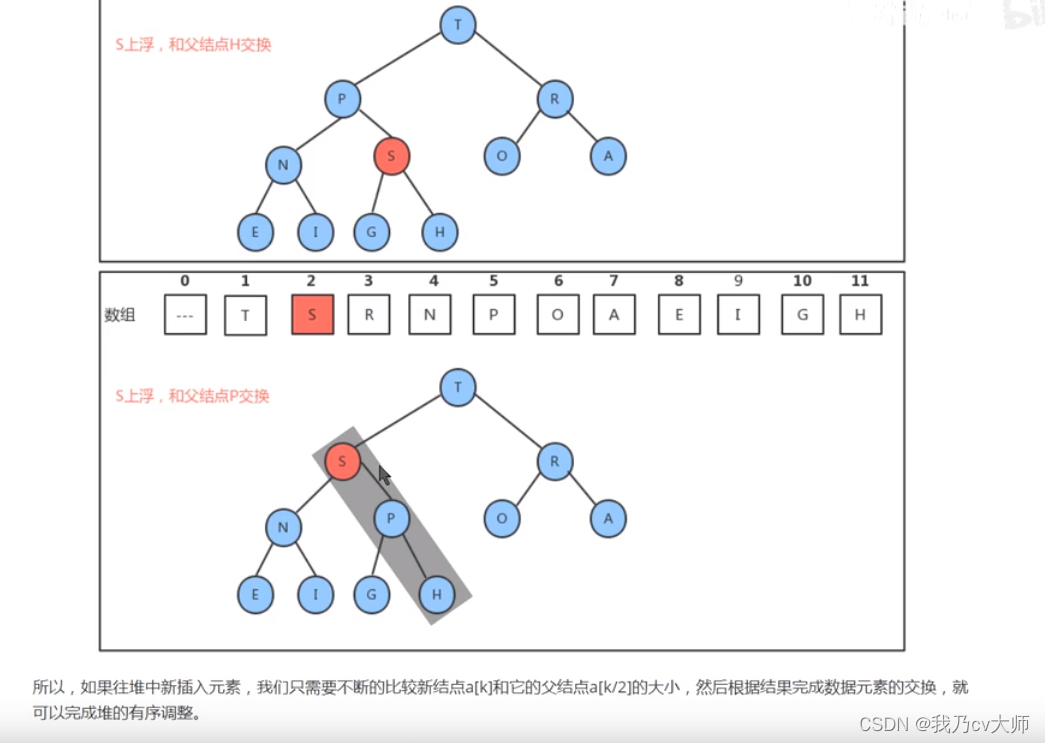
 堆的删除：

以删除根节点为例，将堆中最后一个元素与根节点元素互换，如图所示

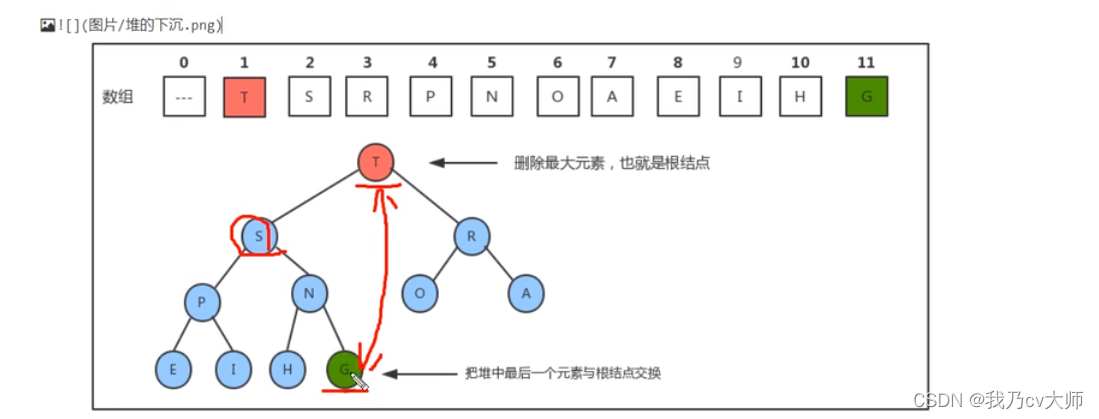
 将置换后的根节点删除，如图所示,

 此时堆并不是标准的堆，要通过不断调整使得堆变成标准堆(下沉操作）,通过逐次下沉操作使得堆变为标准堆

 

 

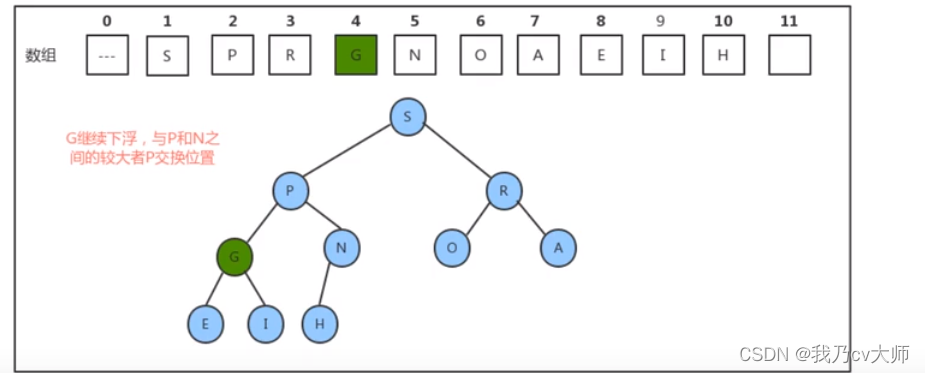
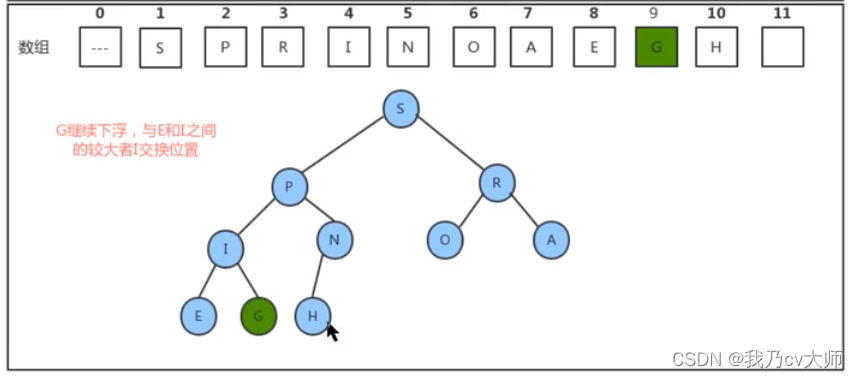
 堆基本操作的代码如下所示，包含堆的插入节点、删除节点、上浮、下沉等算法

public class Heap<T extends Comparable<T>>{
        //存储堆中的元素
        private T[] items;
        //记录堆中元素的个数
     private int N;
     //初始化,数组中的0索引处已经废弃掉了
     public Heap(int capacity){
         this.items=(T[]) new Comparable[capacity+1];
         this.N=0;
     }
     //判断堆中索引i处的元素是否小于索引j处的元素
     private boolean less(int i,int j){
         return items[i].compareTo(items[j])<0;
     }
     //交换堆中i索引和j索引处的值
     private void exch(int i,int j){
         T temp=items[i];
         items[i]=items[j];
         items[j]=temp;
     }
     //往堆中插入一个元素
     public void insert(T t){
         items[++N]=t;
         //使得插入的元素处于正确的位置
         swim(N);
     }
     //使用上浮算法，使得索引k处的元素能在堆中处于一个正确的位置
     public void swim(int k){
         //通过循环，不断比较当前节点的值和父节点的值，如果发现父节点的值比当前节点小，则交换位置
         while (k>1){
             //比较当前节点和其父节点,如果小，则交换两者的位置
             if(less(k/2,k)){
                 exch(k/2,k);
             }
             k=k/2;
         }
 }
 //删除堆中最大的元素，并返回这个最大元素
      public T delMax(){
       T max=items[1];
       //交换索引1处的元素和最大索引处的元素，让完全二叉树的最右侧元素变成临时根节点
        exch(1,N);
          //删除最大索引处的节点
      items[N]=null;
          //元素个数减一
N--;
          //通过下沉调整堆，让堆重新有序
          sink(1);
          return max;
   }
   //使用下沉算法
   public void sink(int k){
         //通过循环不断对比当前k节点及其左子节点2k、右子节点2k+1，如果当前节点小，则需要交换位置
       //存在删除后不存在右子节点的情况

       //-----------------这里的范围非常关键
       while (2*k<=N){
           //-------------------
           //获取当前节点的较大子节点值
           int max;//记录较大节点所在的索引
           if(2*k+1<=N){
               if(less(2*k,2*k+1)){
                   max=2*k+1;
               }
               else {
                   max=2*k;
               }
           }
           else {
               max=2*k;
           }
           //如果已经符合条件
           if(!less(k,max)){
               break;
           }
           //如果不符合条件，则交换k和max索引处的值
           exch(k,max);
           //k往下走
           k=max;

       }
   }

 }

时间复杂度，空间复杂度分析见排序算法之 堆排序 及其时间复杂度和空间复杂度_庾志辉的博客-CSDN博客_堆排序时间复杂度

具体原理,代码实现见

Java实现堆排序及详细图解_又蠢又笨的懒羊羊程序猿的博客-CSDN博客