. - 力扣(LeetCode)
题目
树可以看成是一个连通且 无环 的 无向 图。
给定往一棵 n 个节点 (节点值 1~n) 的树中添加一条边后的图。添加的边的两个顶点包含在 1 到 n 中间,且这条附加的边不属于树中已存在的边。图的信息记录于长度为 n 的二维数组 edges ,edges[i] = [ai, bi] 表示图中在 ai 和 bi 之间存在一条边。
请找出一条可以删去的边,删除后可使得剩余部分是一个有着 n 个节点的树。如果有多个答案,则返回数组 edges 中最后出现的那个。
示例 1:
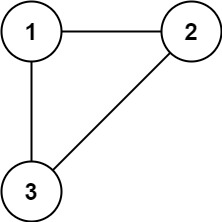
输入: edges = [[1,2], [1,3], [2,3]] 输出: [2,3]
示例 2:
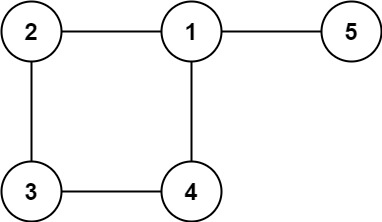
输入: edges = [[1,2], [2,3], [3,4], [1,4], [1,5]] 输出: [1,4]
解题方法
- 这个解题方法没有推导之类的技巧,需要记住使用“并查集”来解决。
- 什么是“并查集”呢?在计算机科学中,并查集(英文:Union-find Disjoint-set data structure,直译为合并查询无交集数据结构)是一种数据结构,通过查询,合并一些无交集数据的问题。
- 经典“并查集”题目:若某个家族人员过于庞大,现在给出家族人数为
,实际存在的
条亲戚关系,询问另外的
对亲戚关系是否成立?
- 题目中给出的图是“给定往一棵
n个节点 (节点值1~n) 的树中添加一条边后的图”,
- 根据树的常识可以知道一个有n个节点的树,有n-1条边。
- 题目中的图,则是n个节点, n-1+1=n条边,即给定边的个数 即为 节点的个数。
直接编码如下:
class Solution:
def findRedundantConnection(self, edges: List[List[int]]) -> List[int]:
n = len(edges)
# 定义关系集合
relataions = [[i] for i in range(1, n+1)]
for edge in edges:
node_0 = edge[0]
node_1 = edge[1]
# 逐条更新关系集合
if relataions[node_0 - 1] != relataions[node_1 - 1]:
index = min(relataions[node_0 - 1], relataions[node_1 - 1])
max_index = max(relataions[node_0 - 1], relataions[node_1 - 1])
relataions = [index if i == max_index else i for i in relataions ]
else:
return edge # 返回多余边
return []时间复杂度分析
- 边的个数记为n,可以看到每遍历一个边关系,就对relations数组进行一次全量更新,因此时间复杂度为
标准并查集写法(优化更新relations数组的方式)
class Solution:
def findRedundantConnection(self, edges: List[List[int]]) -> List[int]:
n = len(edges)
relataions = [i for i in range(n+1)] # 多一个无效的relations[0]元素,便于后续索引操作
def find(index: int) -> int:
if relataions[index] != index:
relataions[index] = find(relataions[index])
return relataions[index]
def union(index_1: int, index_2: int):
relataions[find(index_1)] = find(index_2)
for node1, node2 in edges:
if find(node1) != find(node2):
# node1 和 node2 当前不在一个集合中,此关系是有效的新关系,则更新关系状态
union(node1, node2)
else:
return [node1, node2]
return []
时间复杂度分析:
- 交集时仅操作单个元素,因此时间复杂度为
AI如何解答这道题呢?
智谱清言 正确的解答了这道题目,只是在并集操作上多存储了一个rank数组,略显复杂。
又是被AI替代的一天啊
def findRedundantConnection(edges):
def find(parent, x):
if parent[x] != x:
parent[x] = find(parent, parent[x]) # 路径压缩
return parent[x]
def union(parent, rank, x, y):
rootX = find(parent, x)
rootY = find(parent, y)
if rootX != rootY:
if rank[rootX] > rank[rootY]:
parent[rootY] = rootX
elif rank[rootX] < rank[rootY]:
parent[rootX] = rootY
else:
parent[rootY] = rootX
rank[rootX] += 1
return False
return True
parent = {}
rank = {}
for a, b in edges:
if a not in parent:
parent[a] = a
rank[a] = 0
if b not in parent:
parent[b] = b
rank[b] = 0
for a, b in edges:
if union(parent, rank, a, b):
return [a, b]
# 示例
edges = [[1,2], [1,3], [2,3]]
print(findRedundantConnection(edges)) # 输出: [2, 3]