学习了S4模型后，简单看一下S5模型。

来自两篇文章的摘要

苏神在文章《重温状态空间模型SSM：HiPPO的高效计算（S4）》中简单提到了S5模型：

由于 HiPPO 的推导是基于u(t)是一维函数进行的，所以到目前为止，S4 的输入uk也都还是标量。那么 S4 怎么处理向量序列输入呢？
非常暴力，它直接对每个分量独立地应用一遍前述线性状态方程，每个方程使用不同的Δ, B, C参数，然后将结果拼接起来，这个做法直到作者最新的 Mamba 依然还被应用。
当然，也有简化的做法，直接在单个 RNN 中处理向量输入，只需要相应地将 B, C改为矩阵就行，这就是 S5 （作者不是 Albert Gu 了），这种做法可以理解为单纯借用了 S4 的线性 RNN 形式以及 HiPPO 的矩阵A，而抛开了 HiPPO 的其他细枝末节，也取得了不错的效果。

Mamba 对向量的处理方式

《一文通透想颠覆Transformer的Mamba：从SSM、HiPPO、S4到Mamba》中也提到Mamba的这种处理方式：

每个序列中每个token的维度为D，Mamba 的处理方式是，给这 D 个 dimension的每个 dimension 都搞一个独立的 SSM，即SSM被独立地应用于每个通道(To operate over an input sequence 𝑥 of batch size 𝐵 and length 𝐿 with 𝐷 channels, the SSM is applied independently to each channel)

如何理解：“每个 dimension 都搞一个独立的 SSM”这点呢？
比如在transformer论文中，一个token便有512大小的维度，如此便可以为每个维度均创建一个状态空间SSM，且每个维度之间彼此独立
其实这个做法也类似transformer中的多头注意力，头与头之间彼此独立，夸张点说，虽然在transformer论文中，每个token有8个注意力头(每个头的维度为64)，但你如果要弄成512个注意力头 也没人会拦着你(每个头的维度为1)

S5 论文速读

S5模型来自文章《Simplified State Space Layers for Sequence Modeling》
文章链接：https://arxiv.org/abs/2208.04933 https://ar5iv.labs.arxiv.org/html/2208.04933

定义

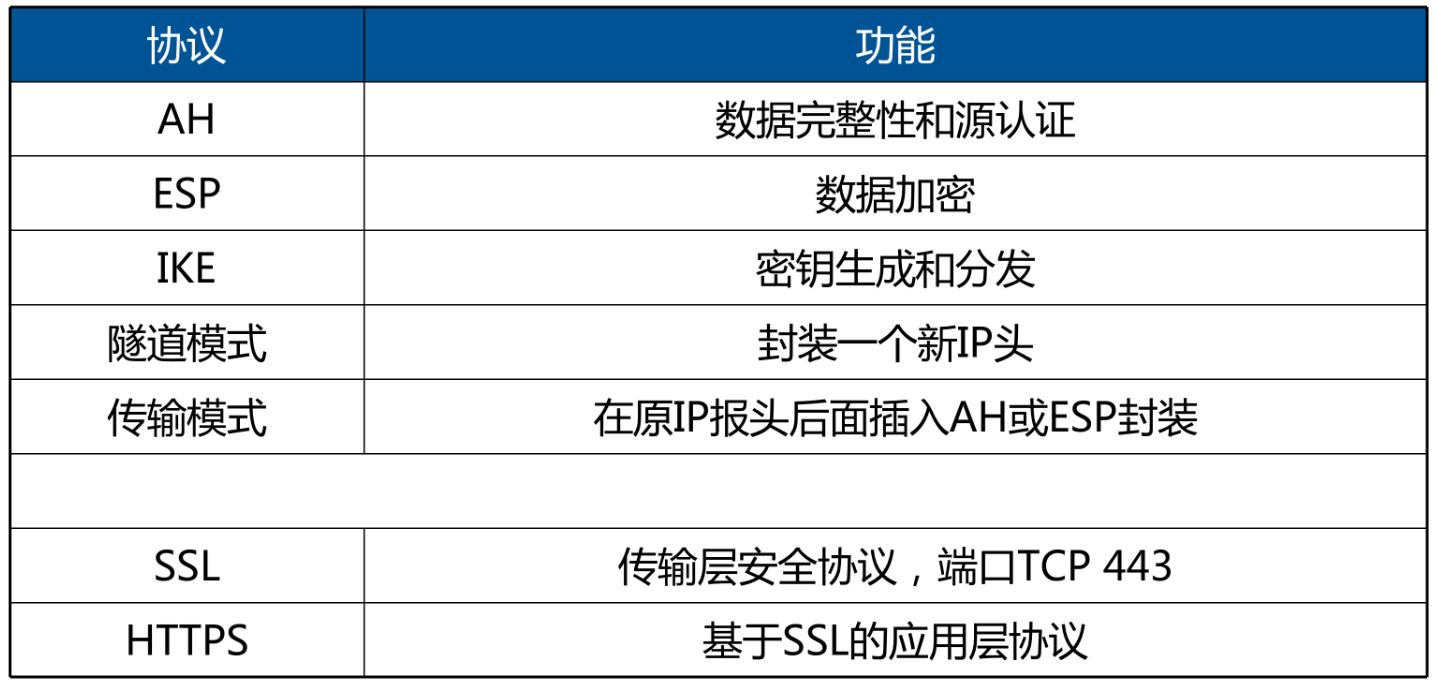
S4：structured state space sequence model
S5：Parallelizing Linear State Space Models With Scans

摘要

使用结构化状态空间序列（S4）层的模型在长距离序列建模任务中取得了最先进的性能。S4层结合了线性状态空间模型（SSM）、HiPPO框架和深度学习来实现高性能。我们以S4层的设计为基础，引入了一个新的状态空间层，即S5层。S4层使用许多独立的单输入、单输出SSM，而S5层使用一个多输入、多输出SSM。我们在S5和S4之间建立了一个连接，并利用它来开发S5模型所使用的初始化和参数化。其结果是，状态空间层可以利用高效且广泛实施的并行扫描，使S5的计算效率与S4相匹配，同时在几个远程序列建模任务上实现了最先进的性能。S5在远程竞技场基准测试中的平均得分为87.4%，在最困难的Path-X任务中的平均分为98.5%。

介绍

高效地对长序列进行建模是机器学习中的一个挑战性问题。解决任务所需的信息可能编码在相隔数千个时间步长的观测之间。为了解决这一问题，已经开发了专门化的循环神经网络（RNNs）、卷积神经网络（CNNs）和transformers的变体。特别是，为了解决标准transformers在序列长度上的二次复杂度问题，引入了许多高效的transformers方法，但这些更高效的变换器在非常长的序列任务上的表现仍然不佳。

Gu等人（2021a）提出了一种使用结构化状态空间序列（S4）层的替代方法。S4层通过许多独立的单输入单输出（SISO）线性状态空间模型（SSMs）来定义非线性序列到序列的转换，并通过非线性混合层将它们耦合在一起。每个SSM利用HiPPO框架通过使用特别构建的状态矩阵进行初始化。由于SSMs是线性的，每个层可以等价地实现为卷积，然后可以通过在序列长度上并行化来高效应用。多个S4层可以堆叠在一起创建深度序列模型。这样的模型在长序列建模任务上取得了显著的改进，包括在特别设计的长范围竞技场（LRA）基准测试上，该基准测试旨在严格测试长序列模型。扩展已经显示出在原始音频生成和长电影片段分类方面的良好性能。

文章引入了一种新的状态空间层，即S5层，如图1所示。S5在两个主要方面简化了S4层。首先，S5使用一个多输入多输出（MIMO）SSM代替S4中的许多独立SISO SSM。其次，S5使用高效且广泛实现的并行扫描。这消除了S4使用的卷积和频域方法的需要，后者需要非平凡的卷积核计算。

由此产生的状态空间层具有与S4相同的计算复杂性，但完全以递归方式在时域中操作。然后建立了S4和S5之间的数学关系。这种联系允许继承对S4成功至关重要的HiPPO初始化方案。不幸的是，S4用于初始化的特定HiPPO矩阵不能以数值稳定的方式对角化以供S5使用。然而，与DSS层和S4D层的最新工作一致，我们发现HiPPO矩阵的对角近似可以实现相当的表现。我们将Gu等人（2022）的结果扩展到MIMO设置中，为在S5中使用对角近似提供了理论依据。我们利用S4和S5之间的数学关系来通知参数化和初始化的其他几个方面，我们进行了彻底的消融研究，以探索这些设计选择。

最终的S5层具有许多理想属性。它易于实现，在序列长度上具有线性复杂性，并且可以高效地处理时变SSM和不规则采样的观测（这在S4的卷积实现中是不切实际的）。S5在各种长序列建模任务上实现了最先进的性能，LRA平均为87.4%，在最困难的Path-X任务上达到了98.5%的准确率。

背景

针对S5模型的背景。

S5 Layer

描述了S5的结构、参数化和计算，特别关注这些方面与S4的不同之处




初始化 先前的工作表明，深度状态空间模型的性能对状态矩阵的初始化很敏感。我们在第2.2节中讨论了，为了有效应用并行扫描，状态矩阵必须是对角的。我们也在第2.3节中讨论了，HiPPO-LegS矩阵不能稳定地对角化，但是HiPPO-N矩阵可以。在第4节中，我们将S5的动态与S4联系起来，以建议为什么在MIMO设置中使用类似HiPPO的矩阵进行初始化也可以很好地工作。我们通过实验支持这一点，发现使用HiPPO-N矩阵对角化可以带来良好的性能，并在附录E中进行消融研究，与其他初始化进行比较。我们注意到DSS（Gupta等人，2022）和S4D（Gu等人，2022）层也通过使用HiPPO-N矩阵的对角化在SISO设置中发现强大的性能。

共轭对称性 具有实数条目的可对角化矩阵的复数特征值总是成共轭对出现。我们通过使用一半数量的特征值和潜在状态来强制执行这种共轭对称性。这确保了实数输出，并将并行扫描的运行时间和内存使用减少了一半。这个想法也在Gu等人（2022）中讨论过。

S4与S5之间的关系

现在建立S4和S5之间的联系。在4.1节中，我们展示在特定条件下，S5 SSM的输出可以被看作是某个特定S4系统计算出的潜在状态的投影。这种联系让我们可以继承S4成功的关键——HiPPO初始化方案。不幸的是，S4用于初始化的特定HiPPO矩阵不能以数值稳定的方式对角化，以适应S5使用的高效并行扫描。然而，与DSS（Gupta et al., 2022）和S4D（Gu et al., 2022）层的最新工作一致，我们发现对HiPPO矩阵的对角近似可以实现相当的性能。我们将Gu等人（2022）的结果扩展到MIMO设置中，为在S5中使用对角近似提供了理论依据。我们利用S4和S5之间的数学关系来指导参数化和初始化的其他几个方面，并且我们进行了彻底的消融研究来探索这些设计选择。