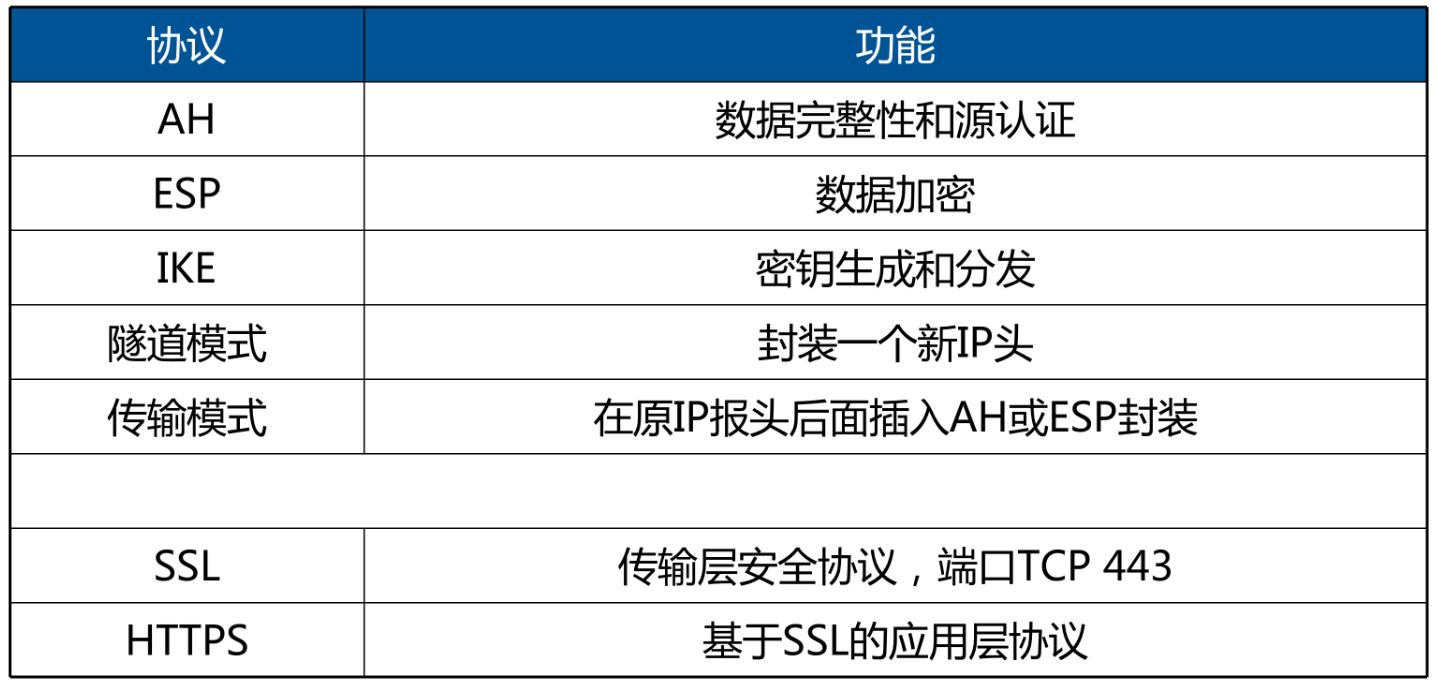
前置知识

若一个游戏满足：

1. 由两名玩家交替行动
2. 在游戏进行的任意时刻，可以执行的合法行动与轮到哪位玩家无关
3. 不能行动的玩家判负

则称该游戏为一个公平组合游戏。

尼姆游戏（NIM）属于公平组合游戏，但常见的棋类游戏，比如围棋就不是公平组合游戏，因为围棋交战双方分别只能落黑子和白子，胜负判定也比较负责，不满足条件2和3。

以下题目均属于公平组合游戏

题目一

解题思路

a_i代表一种情况，a₁^a~2~a₃^…a_n = 0代表先手必输情况；
a₁^a~2~a₃^…a_n ≠ 0 代表先手必胜情况
（公式，背就完了）

代码实现

#include<iostream>

using namespace std;

int main()
{
    int res = 0;
    int n = 0;
    
    cin >> n;
    while (n -- )
    {
        int x;
        scanf("%d", &x);
        res ^= x;
    }
    
    if (res)
    {
        cout <<"Yes";
    }
    else
    {
        cout << "No";
    }
    return 0;
}

题目二

解题思路

不严谨的思路：
移动偶数级台阶的石子是没有意义的，比如我把偶数级的石头移到下一级（即奇数级），对方又可以把其再移动到下一级（即偶数级）上，这样奇数级上的石子数量是保持不变的，因此这对我取胜是没有帮助的，移动了也等于没有移动。但如果我移动的是奇数级台阶上的石子，比如只有第一级有石子，我将第一级的石子移动到地面，我就赢了，所以真正影响胜负的是奇数级台阶的石子。

代码实现

#include<iostream>

using namespace std;

int main()
{
    int n;
    cin >> n;
    
    int res = 0;
    for (int i = 1; i <= n; i ++)
    {
        int x;
        scanf("%d", &x);
        if (i % 2 != 0)
        {
            res ^= x;
        }
    }
    
    if (res)
    {
        cout << "Yes";
    }
    else
    {
        cout<< "No";
    }
    return 0;
}

题目三

解题思路

原题解链接：https://www.acwing.com/solution/content/23435/

代码实现

#include<iostream>
#include<cstring>
#include<algorithm>
#include<set>//任意map都行

using namespace std;

const int N=110,M=10010;
int n,m;
int f[M],s[N];//s存储的是可供选择的集合,f存储的是所有可能出现过的情况的sg值

int sg(int x)
{
    if (f[x] != -1) return f[x];
    //因为取石子数目的集合是已经确定了的,所以每个数的sg值也都是确定的,如果存储过了,直接返回即可
    set<int> S;
    //set代表的是有序集合(注:因为在函数内部定义,所以下一次递归中的S不与本次相同)
    for (int i = 0; i < m; i ++ )
    {
        int sum = s[i];
        if (x >= sum) S.insert(sg(x-sum));
        //先延伸到终点的sg值后,再从后往前排查出所有数的sg值
    }

    for (int i = 0; ; i ++ )
    //循环完之后可以进行选出最小的没有出现的自然数的操作
     if (!S.count(i))
      return f[x] = i;
}

int main()
{
    cin >> m;
    for (int i = 0; i < m; i ++ )
    cin >> s[i];

    cin >> n;
    memset(f,-1,sizeof(f));//初始化f均为-1,方便在sg函数中查看x是否被记录过

    int res = 0;
    for(int i = 0; i < n; i ++ )
    {
        int x;
        cin >> x;
        res ^= sg(x);
        //观察异或值的变化,基本原理与Nim游戏相同
    }

    if (res) printf("Yes");
    else printf("No");

    return 0;
}